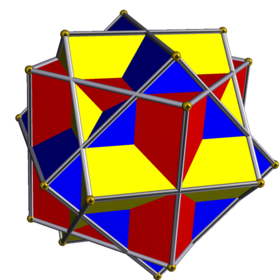
Соединение трёх кубиков

Соединение трёх кубиков

Тип	Однородный состав
Индекс	УК ₈
Выпуклая оболочка	Неоднородный усеченный октаэдр
Многогранники	3 кубика
Лица	6+12 квадратов
Края	36
Вершины	24
Группа симметрии	октаэдрический ( о _ч )
Подгруппа, ограничивающаяся одним компонентом	4-кратный призматический ( D _4h )

В геометрии соединение трех кубов представляет собой однородное многогранное соединение, образованное тремя кубами, расположенными с октаэдрической симметрией . ^[1] Это было изображено в работах Макса Брюкнера и М. К. Эшера .

История

Это соединение появляется в Макса Брюкнера книге «Многоугольники и многогранники» (1900). ^[2] и в литографии « Водопад » (1961) М.К. Эшера , который узнал о нем из книги Брюкнера. Его двойник , соединение трех октаэдров , образует центральное изображение в более ранней гравюре » Эшера на дереве «Звезды . ^[3]

В рукописи XV века De quinque corporibus Regularibus Пьеро делла Франческа включает рисунок октаэдра, описанного вокруг куба, причем восемь ребер куба лежат на восьми гранях октаэдра. Три куба, вписанные таким образом в один октаэдр, образовали бы соединение трех кубов, но делла Франческа не изображает это соединение. ^[4]

Куб в октаэдре из пяти правильных тел Де

Другой вид куба в октаэдре

Конструкция и координаты

Это соединение можно построить, наложив друг на друга три одинаковых куба, а затем повернув каждый на 45 градусов вокруг отдельной оси (проходящей через центры двух противоположных граней). ^[3]

Декартовы координаты вершин этого соединения можно выбрать как перестановки все $(0,\pm 1,\pm {\sqrt {2}})$ .

Ссылки

^ Верхейен, Хьюго Ф. (1996), «Глава 4: Классификация конечных соединений кубов», Орбиты симметрии , Коллекция Design Science, Бостон: Birkhäuser, стр. 95–159, doi : 10.1007/978-1-4612-4074 -7_5 , ISBN 0-8176-3661-7 , МР 1363715 ; см., в частности, стр. 136 .
^ Брюкнер, Макс (1900), Многоугольники и многогранники, Теория и история , Лейпциг: Б. Г. Тойбнер, Табличка 23
^ Jump up to: Перейти обратно: ^а ^б Харт, Джордж В. , «Вундеркаммер бумажных многогранников Макса Брюкнера», Материалы конференции Bridges 2019 (PDF) , стр. 59–66
^ Харт, Джордж В. (1998), «Многогранники Пьеро делла Франчески», Виртуальные многогранники .

[verheyen-1] Верхейен, Хьюго Ф. (1996), «Глава 4: Классификация конечных соединений кубов», Орбиты симметрии , Коллекция Design Science, Бостон: Birkhäuser, стр. 95–159, doi : 10.1007/978-1-4612-4074 -7_5 , ISBN 0-8176-3661-7 , МР 1363715 ; см., в частности, стр. 136 .

[bruckner-2] Брюкнер, Макс (1900), Многоугольники и многогранники, Теория и история , Лейпциг: Б. Г. Тойбнер, Табличка 23

[h19-3] Jump up to: Перейти обратно: ^а ^б Харт, Джордж В. , «Вундеркаммер бумажных многогранников Макса Брюкнера», Материалы конференции Bridges 2019 (PDF) , стр. 59–66

[h98-4] Харт, Джордж В. (1998), «Многогранники Пьеро делла Франчески», Виртуальные многогранники .

[1]

[2]

[3]

[4]