Подгруппа
| Алгебраическая структура → Теория групп Теория групп |
|---|
 |
В теории групп , разделе математики , для группы G при бинарной операции ∗ подмножество H группы G называется подгруппой G , если H также образует группу при операции ∗. Точнее, H является подгруппой G , если ограничение * на H × H является групповой операцией на H . Это часто обозначается H ≤ G , что читается как « H является подгруппой G ».
Тривиальной подгруппой любой группы является подгруппа { e }, состоящая только из единичного элемента. [1]
Собственная подгруппа группы G — это подгруппа H , которая является собственным подмножеством группы G (т. е. H ≠ G ). Это часто обозначается как H < G , что читается как « H является собственной подгруппой G ». Некоторые авторы также исключают из числа собственных тривиальную группу (т. е. H ≠ { e }). [2] [3]
Если H подгруппа группы G , то G иногда называют надгруппой группы H. —
Те же определения применяются в более общем смысле, когда G — произвольная полугруппа , но в этой статье будут рассматриваться только подгруппы групп.
Подгрупповые тесты [ править ]
Предположим, что — группа, а H — подмножество G. G А пока предположим, что групповая операция G записана мультипликативно и обозначается сопоставлением.
- Тогда H является подгруппой группы G тогда и только тогда, когда H непуста и замкнута относительно произведений и обратных групп. Закрытость под продуктами что для каждых a и b в H продукт ab находится в H. означает , Замкнутость относительно инверсий означает, что для каждого a в H инверсия a −1 в Х. находится Эти два условия можно объединить в одно: для каждого a и b в H элемент ab −1 находится в H , но это более естественно и обычно так же легко проверить два условия замыкания по отдельности. [4]
- Когда H конечна . , тест можно упростить: H является подгруппой тогда и только тогда, когда она непуста и замкнута относительно произведений Уже из этих условий следует, что каждый элемент a из H порождает конечную циклическую подгруппу из H , порядка n , и тогда обратным к a является , скажем п -1 . [4]
Если вместо этого групповая операция обозначается сложением, то замкнутая относительно произведений должна быть заменена закрытой относительно сложенной , что является условием того, что для каждых a и b в H сумма a + b находится в H и замкнутая относительно обратных операций должна быть отредактировано, чтобы сказать, что для каждого a в H обратное значение − a находится в H .
Основные свойства подгрупп [ править ]
- Идентичность подгруппа подгруппы является тождеством группы: если — с единицей а , H — G с единицей eH G , то eH eG = eG группа .
- Обратный H это обратный элемент в группе: если элемент в подгруппе — — подгруппа группы G , а a и b — элементы H такие, что ab = ba = e H , то ab = ba = е Г.
- Если H — подгруппа группы G , то отображение включения H → G, переводящее каждый элемент a группы H в себя, является гомоморфизмом .
- Пересечение снова является подгрупп A и B группы G подгруппой G . [5] Например, пересечение осей X и Y в при сложении — тривиальная подгруппа. В более общем смысле, пересечение произвольного набора подгрупп G является подгруппой G .
- Объединение подгрупп когда A и B является подгруппой тогда и только тогда, A ⊆ B или B ⊆ A . Непример: не является подгруппой потому что 2 и 3 являются элементами этого подмножества, сумма которых 5 не входит в подмножество. Аналогично, объединение осей x и осей y в не является подгруппой
- Если S является подмножеством G , то существует наименьшая подгруппа, содержащая S , а именно пересечение всех подгрупп, содержащих S ; она обозначается ⟨ S ⟩ и называется подгруппой, порожденной S . Элемент G находится в ⟨ S ⟩ тогда и только тогда, когда он является конечным произведением элементов S и их обратных, возможно, повторяющихся. [6]
- Каждый элемент a группы G порождает циклическую подгруппу ⟨ a ⟩ . Если ⟨ a ⟩ изоморфно ( целые числа по модулю n ) для некоторого положительного целого числа n , тогда n — наименьшее положительное целое число, для которого н = e , n называется порядком a а . Если ⟨ a ⟩ изоморфно тогда а говорят, что имеет бесконечный порядок .
- Подгруппы любой данной группы образуют полную решетку по включению, называемую решеткой подгрупп . (Хотя нижняя грань здесь представляет собой обычное теоретико-множественное пересечение, верхняя грань множества подгрупп — это подгруппа, порожденная теоретико-множественным объединением подгрупп, а не само теоретико-множественное объединение.) Если e — тождество G , то тривиальная группа { e } является минимальной подгруппой G , а максимальная группа G. подгруппа — это сама

Лагранжа Классы смежности и теорема
Учитывая подгруппу H и некоторый a в G , мы определяем левый смежный класс aH = { ah : h в H }. Поскольку a обратимо, отображение φ : H → aH, заданное формулой φ( h ) = ah, является биекцией . Более того, каждый элемент G содержится ровно в одном левом смежном классе H ; левые смежные классы являются классами эквивалентности, соответствующими отношению эквивалентности a 1 ~ a 2 тогда и только тогда, когда в Х. находится Число левых смежных классов H называется индексом H и в G обозначается [ G : H ] .
Теорема Лагранжа что для конечной группы G и подгруппы H утверждает ,
где | г | и | Ч | обозначают порядки G H и соответственно . В частности, порядок каждой подгруппы G (и порядок каждого элемента G должен быть делителем | ) г | . [7] [8]
Правые смежные классы определяются аналогично: Ha = { ha : h in H }. Они также являются классами эквивалентности для подходящего отношения эквивалентности, и их число равно [ G : H ] .
Если aH = Ha для любого a из G , то H называется нормальной подгруппой . Каждая подгруппа индекса 2 нормальна: левые смежные классы, а также правые смежные классы представляют собой просто подгруппу и ее дополнение. В более общем смысле, если p — наименьшее простое число, делящее порядок конечной группы G , то любая подгруппа индекса p (если таковая существует) является нормальной.
Пример: Подгруппы Z 8 [ править ]
Пусть G — циклическая группа Z8 , элементами которой являются
и чья групповая операция — сложение по модулю 8 . Его Кэли таблица
| + | 0 | 4 | 2 | 6 | 1 | 5 | 3 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 4 | 2 | 6 | 1 | 5 | 3 | 7 |
| 4 | 4 | 0 | 6 | 2 | 5 | 1 | 7 | 3 |
| 2 | 2 | 6 | 4 | 0 | 3 | 7 | 5 | 1 |
| 6 | 6 | 2 | 0 | 4 | 7 | 3 | 1 | 5 |
| 1 | 1 | 5 | 3 | 7 | 2 | 6 | 4 | 0 |
| 5 | 5 | 1 | 7 | 3 | 6 | 2 | 0 | 4 |
| 3 | 3 | 7 | 5 | 1 | 4 | 0 | 6 | 2 |
| 7 | 7 | 3 | 1 | 5 | 0 | 4 | 2 | 6 |
Эта группа имеет две нетривиальные подгруппы: ■ J = {0, 4} и ■ H 0, 4, 2, 6} , где J также является подгруппой H. = { Таблица Кэли для H — это верхний левый квадрант таблицы Кэли для G ; Таблица Кэли для J — это верхний левый квадрант таблицы Кэли H. для Группа G циклическая . , как и ее подгруппы В общем случае подгруппы циклических групп также являются циклическими. [9]
Пример: Подгруппы S 4 [ править ]
S 4 — симметричная группа , элементы которой соответствуют перестановкам 4 элементов.
Ниже приведены все его подгруппы, упорядоченные по мощности.
Каждая группа (кроме групп мощности 1 и 2) представлена своей таблицей Кэли .
24 элемента [ править ]
Как и каждая группа, S 4 является своей подгруппой.
 |
12 элементов [ править ]
Альтернирующая группа содержит только четные перестановки .
Это одна из двух нетривиальных собственных подгрупп группы S4 . нормальных (Вторая — ее подгруппа Клейна.)

Подгруппы:





8 элементов [ править ]
 Подгруппы:   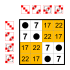 |  Подгруппы: 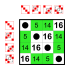  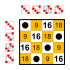 |  Подгруппы: 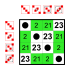  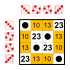 |
6 элементов [ править ]
 Подгруппа:  |  Подгруппа:  |  Подгруппа:  |  Подгруппа:  |
4 элемента [ править ]
 |  |  |  ( нормальная подгруппа ) |
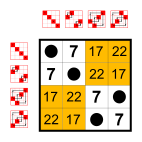 |  |  |
3 элемента [ править ]
 | 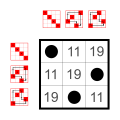 | 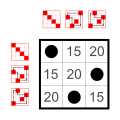 | 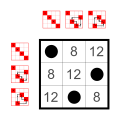 |
2 элемента [ править ]
Каждая перестановка p порядка 2 порождает подгруппу {1, p }.Это перестановки, которые имеют только 2 цикла:
- Всего существует 6 транспозиций с одним 2-циклом. (зеленый фон)
- И 3 перестановки с двумя 2-циклами. (белый фон, жирные цифры)
1 элемент [ править ]
Тривиальная подгруппа — это единственная подгруппа порядка 1.
Другие примеры [ править ]
- Четные целые числа образуют подгруппу целочисленного кольца сумма двух четных целых чисел четна, а отрицательное число четного числа четно.
- Идеал — в кольце R это подгруппа аддитивной группы R. кольца
- Линейное подпространство векторного пространства — это подгруппа аддитивной группы векторов.
- В абелевой группе элементы конечного порядка образуют подгруппу, называемую периодической подгруппой .
См. также [ править ]
- Картановая подгруппа
- Подгруппа фитингов
- Подгруппа фиксированной точки
- Полностью нормализованная подгруппа
- Стабильная подгруппа
Примечания [ править ]
- ^ Галлиан 2013 , с. 61.
- ^ Хангерфорд 1974 , с. 32.
- ^ Артин 2011 , с. 43.
- ^ Jump up to: Перейти обратно: а б Курцвейл и Штелмахер 1998 , с. 4.
- ^ Джейкобсон 2009 , с. 41.
- ^ Эш 2002 .
- ^ См . дидактическое доказательство в этом видео .
- ^ Даммит и Фут 2004 , с. 90.
- ^ Галлиан 2013 , с. 81.
Ссылки [ править ]
- Джейкобсон, Натан (2009), Основная алгебра , том. 1 (2-е изд.), Дувр, ISBN 978-0-486-47189-1 .
- Хангерфорд, Томас (1974), Алгебра (1-е изд.), Springer-Verlag, ISBN 9780387905181 .
- Артин, Майкл (2011), Алгебра (2-е изд.), Прентис Холл, ISBN 9780132413770 .
- Даммит, Дэвид С.; Фут, Ричард М. (2004). Абстрактная алгебра (3-е изд.). Хобокен, Нью-Джерси: Уайли. ISBN 9780471452348 . OCLC 248917264 .
- Галлиан, Джозеф А. (2013). Современная абстрактная алгебра (8-е изд.). Бостон, Массачусетс: Обучение Брукса / Коула Сенгеджа. ISBN 978-1-133-59970-8 . OCLC 807255720 .
- Курцвейл, Ганс; Штелмахер, Бернд (1998). Теория конечных групп . Учебник Спрингера. дои : 10.1007/978-3-642-58816-7 .
- Эш, Роберт Б. (2002). Абстрактная алгебра: основной выпускной год . Департамент математики Университета Иллинойса.









![{\displaystyle [G:H]={|G| \над |H|}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e64b76d0605e6c7891273e65da28b5e431d4ea4)




