Альтернативная группа
Эта статья включает список общих ссылок , но в ней отсутствуют достаточные соответствующие встроенные цитаты . ( январь 2008 г. ) |
| Алгебраическая структура → Теория групп Теория групп |
|---|
 |
В математике — знакопеременная группа это группа четных перестановок конечного множества . Знакомая группа на множестве из n элементов называется знакопеременной группой степени n или знакопеременной группой из n букв обозначается An и или Alt( n ).
Основные свойства [ править ]
При n > 1 группа An является коммутантом симметрической группы Sn с индексом 2 имеет и, следовательно, n ! /2 элемента. Это ядро гомоморфизма сигнатурной группы sn : Sn → {1, −1}, объясняемого в терминах симметричной группы .
Группа An абелева n тогда и только тогда, когда ⩽ 3 , и простая тогда и только тогда, когда n = 3 или n ≥ 5 . A 5 — наименьшая неабелева простая группа , имеющая порядок 60, и наименьшая неразрешимая группа .
Группа A 4 имеет четырехгруппу Клейна V как собственную нормальную подгруппу , а именно единицу и двойные транспозиции { (), (12)(34), (13)(24), (14)(23) } , это ядро сюръекции A 4 на A 3 ≅ Z 3 . Имеем точную последовательность V → A 4 → A 3 = Z 3 . В теории Галуа это отображение, а точнее соответствующее отображение S 4 → S 3 , соответствует сопоставлению резольвентной кубики Лагранжа с квартикой, что позволяет полином четвертой степени решать радикалами, как установил Лодовико Феррари .
Классы сопряженности [ править ]
Как и в симметричной группе , любые два элемента An , сопряженные элементом An , должны иметь одинаковую форму цикла . Однако обратное не обязательно верно. Если форма цикла состоит только из циклов нечетной длины и нет двух циклов одинаковой длины, где циклы длины один включены в тип цикла, то для этой формы цикла существует ровно два класса сопряженности ( Скотт 1987 , §11.1, стр. 299). ).
Примеры:
- Две перестановки (123) и (132) не являются сопряженными в A 3 , хотя они имеют одинаковую форму цикла и, следовательно, сопряжены в S 3 .
- Перестановка (123)(45678) не сопряжена с обратной ей (132)(48765) в A 8 , хотя обе перестановки имеют одинаковую форму цикла, поэтому они сопряжены в S 8 .
Связь с симметричной группой [ править ]
- См. Симметричная группа .
Поскольку конечные симметрические группы — это группы всех перестановок множества с конечными элементами, а знакопеременные группы — это группы четных перестановок, знакопеременные группы — это подгруппы конечных симметрических групп.
Генераторы и отношения [ править ]
При n ≥ 3 An порождается 3-циклами, поскольку 3-циклы можно получить путем объединения пар транспозиций. Этот набор генераторов часто используется для доказательства того, что An прост для n ≥ 5 .
Группа автоморфизмов [ править ]
| н | Аут(А н ) | Выход(А н ) |
|---|---|---|
| п ≥ 4, п ≠ 6 | С н | З 2 |
| п = 1, 2 | З 1 | З 1 |
| п = 3 | З 2 | З 2 |
| п = 6 | С 6 ⋊ З 2 | В = Z 2 × Z 2 |
Для n > 3 за исключением n 6 , группой автоморфизмов An ; является симметрическая группа Sn с внутренней группой автоморфизмов An и = внешней группой автоморфизмов Z 2 , внешний автоморфизм возникает в результате сопряжения нечетной перестановкой.
При n = 1 и 2 группа автоморфизмов тривиальна. Для n = 3 группа автоморфизмов равна Z 2 с тривиальной внутренней группой автоморфизмов и внешней группой автоморфизмов Z 2 .
Внешняя группа автоморфизмов A 6 представляет собой четырехгруппу Клейна V = Z 2 × Z 2 и связана с внешним автоморфизмом S 6 . Дополнительный внешний автоморфизм в A 6 заменяет 3-циклы (типа (123)) элементами формы 3. 2 (например, (123)(456) ).
Исключительные изоморфизмы [ править ]
Существуют некоторые исключительные изоморфизмы между некоторыми малыми знакопеременными группами и малыми группами лиева типа , в частности, проективными специальными линейными группами . Это:
- A 4 изоморфен PSL 2 (3) [1] и группа симметрии киральной тетраэдрической симметрии .
- A 5 изоморфен PSL 2 (4), PSL 2 (5) и группе симметрии киральной икосаэдрической симметрии . (Видеть [1] для косвенного изоморфизма PSL 2 (F 5 ) → A 5 с использованием классификации простых групп порядка 60, а здесь и для прямого доказательства).
- A 6 изоморфен PSL 2 (9) и PSp 4 (2)'.
- A 8 изоморфен PSL 4 (2).
Более очевидно, что A 3 изоморфна циклической группе Z 3 , а A 0 , A 1 и A 2 изоморфны тривиальной группе (которая также является SL 1 ( q ) = PSL 1 ( q ) для любого q ).
Примеры S 4 и A 4 [ править ]
 Нечетные перестановки окрашены в цвет: Транспозиции показаны зеленым цветом, а 4-циклы - оранжевым. |  Элементы: четные перестановки (тождество, восемь 3-циклов и три двойные транспозиции (двойные транспозиции выделены жирным шрифтом)) Подгруппы:      |
 A3 ( = Z3 ) порядок 3 | 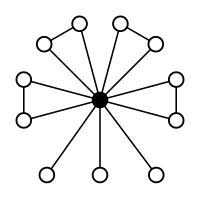 А 4 (заказ 12) | 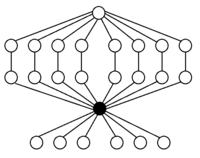 А 4 × Z 2 (порядок 24) |
 S 3 = Dih 3 (порядок 6) |  С 4 (заказ 24) |  А 4 в S 4 слева |
Пример A 5 как подгруппа трехмерных вращений [ править ]


A 5 — группа изометрий додекаэдра в 3-пространстве, поэтому существует представление A 5 → SO 3 ( R ) .
На этом рисунке вершины многогранников представляют элементы группы, а центр сферы представляет собой единичный элемент. Каждая вершина представляет собой вращение вокруг оси, направленной от центра к этой вершине, на угол, равный расстоянию от начала координат в радианах. Вершины одного и того же многогранника принадлежат к одному классу сопряженности. Поскольку уравнение класса сопряженности для A 5 равно 1 + 12 + 12 + 15 + 20 = 60 , мы получаем четыре различных (нетривиальных) многогранника.
Вершины каждого многогранника находятся в биективном соответствии с элементами его класса сопряженности, за исключением класса сопряженности (2,2)-циклов, который на внешней поверхности представлен икосододекаэдром, антиподальные вершины которого отождествляются с друг друга. Причина этой избыточности заключается в том, что соответствующие вращения совершаются на π радиан и поэтому могут быть представлены вектором длины π в любом из двух направлений. Таким образом, класс (2,2)-циклов содержит 15 элементов, а икосододекаэдр — 30 вершин.
Два класса сопряжения двенадцати 5-циклов в A 5 представлены двумя икосаэдрами радиусов 2 π /5 и 4 π /5 соответственно. Нетривиальный внешний автоморфизм в Out(A 5 ) ≃ Z 2 меняет местами эти два класса и соответствующие икосаэдры.
Пример: головоломка «15» [ править ]
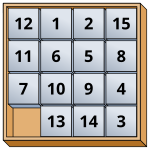
Можно доказать, что головоломка 15 , известный пример скользящей головоломки , может быть представлена чередующейся группой A 15 , [2] потому что комбинации головоломки 15 могут быть созданы с помощью 3-х циклов . Фактически, любую раздвижную головоломку размером 2 k − 1 с квадратными плитками одинакового размера можно представить как A 2 k −1 .
Подгруппы [ править ]
A 4 — наименьшая группа, демонстрирующая, что обратная теорема Лагранжа в общем случае неверна: дана конечная группа G и делитель d группы | G |, не обязательно существует подгруппа G порядка d : группа G = A 4 порядка 12 не имеет подгруппы порядка 6. Подгруппа из трех элементов (порожденная циклическим вращением трех объектов) с любой отдельный нетривиальный элемент порождает всю группу.
Для всех n > 4 An . не имеет нетривиальных (т. е. собственных) подгрупп нормальных Таким образом, An — простая группа для всех n > 4 . 5 . наименьшая неразрешимая группа —
Групповая гомология [ править ]
Групповая гомология знакопеременных групп демонстрирует стабилизацию, как и в стабильной теории гомотопий : при достаточно больших n она постоянна. Однако существуют некоторые исключительные низкоразмерные гомологии. Обратите внимание, что гомологии симметричной группы демонстрируют аналогичную стабилизацию, но без исключений малой размерности (дополнительных элементов гомологии).
H 1 : Абелианизация [ править ]
Первая группа гомологий совпадает с абелианизацией и (поскольку An совершенна , за исключением упомянутых исключений) такова:
- H 1 (A n , Z) = Z 1 для n = 0, 1, 2;
- ЧАС 1 (А 3 , Z) = А аб
3 = А 3 = Z 3 ; - ЧАС 1 (А 4 , Z) = А аб
4 = Z3 ; - H 1 (A n , Z) = Z 1 для n ≥ 5.
Это легко увидеть непосредственно следующим образом. A n генерируется 3-циклами – поэтому единственными нетривиальными отображениями абелианизации являются An поэтому → Z 3 , поскольку элементы порядка 3 должны отображаться в элементы порядка 3 – а для n ≥ 5 все 3-циклы сопряжены, они должны отображаться в один и тот же элемент при абелианизации, поскольку сопряжение тривиально в абелевых группах. Таким образом, 3-цикл типа (123) должен отображаться в тот же элемент, что и его обратный (321), но, таким образом, должен отображаться в единицу, поскольку тогда он должен иметь порядок, разделяющий 2 и 3, поэтому абелианизация тривиальна.
При n < 3 An . тривиален и, следовательно, имеет тривиальную абелианизацию Для A 3 и A 4 можно вычислить абелианизацию напрямую, заметив, что 3-циклы образуют два класса сопряженности (а не все они являются сопряженными) и существуют нетривиальные отображения A 3 ↠ Z 3 (фактически изоморфизм) и A 4 ↠ З 3 .
H 2 : Множители Шура [ править ]
Мультипликаторы Шура знакопеременных групп An ( в случае, когда n не меньше 5) являются циклическими группами порядка 2, за исключением случая, когда n равно либо 6, либо 7, и в этом случае существует также тройное накрытие. В этих случаях мультипликатор Шура имеет (циклическую группу) порядка 6. [3] Впервые они были вычислены в ( Schur 1911 ).
- H 2 (A n , Z) = Z 1 для n = 1, 2, 3;
- Н 2 (А н , Z) = Z 2 для n = 4, 5;
- Н 2 (А н , Z) = Z 6 для n = 6, 7;
- H 2 (A n , Z) = Z 2 для n ≥ 8.
Примечания [ править ]
- ^ Jump up to: Перейти обратно: а б Робинсон (1996), с. 78
- ^ Билер, Роберт. «Загадка пятнадцати: мотивирующий пример для меняющейся группы» (PDF) . факультет.etsu.edu /. Государственный университет Восточного Теннесси. Архивировано из оригинала (PDF) 7 января 2021 г. Проверено 26 декабря 2020 г.
- ^ Уилсон, Роберт (31 октября 2006 г.), «Глава 2: Альтернирующие группы» , Конечные простые группы, версии 2006 г. , заархивировано из оригинала 22 мая 2011 г., 2.7: Накрывающие группы
{{citation}}: CS1 maint: постскриптум ( ссылка )
Ссылки [ править ]
- Робинсон, Дерек Джон Скотт (1996), Курс теории групп , Тексты для аспирантов по математике, том. 80 (2-е изд.), Springer, ISBN 978-0-387-94461-6
- Шур, Иссаи (1911), «О представлении симметричной и знакопеременной группы дробными линейными заменами», Журнал чистой и прикладной математики , 1911 (139): 155–250, doi : 10.1515/crll.1911.139.155 , S2CID 122809608
- Скотт, WR (1987), Теория групп , Нью-Йорк: Dover Publications , ISBN 978-0-486-65377-8
