Модульная группа

В математике модулярная группа — это проективная специальная линейная группа. ${\textstyle \operatorname {PSL} (2,\mathbb {Z} )}$ размера 2 × 2 матриц с целыми коэффициентами и определителем 1. Матрицы $A$ и $- A$ отождествлены. Модульная группа действует в верхней половине комплексной плоскости посредством дробных линейных преобразований , а название «модульная группа» происходит от отношения к пространствам модулей , а не от модулярной арифметики .

Определение [ править ]

Модулярная группа $Г$ — это группа дробно -линейных преобразований верхней половины комплексной плоскости , имеющих вид

z\mapsto {\frac {az+b}{cz+d}}

где $a$ , $b$ , $c$ , $d$ — целые числа, а $ad - bc = 1$ . Групповая операция — это композиция функций .

Эта группа преобразований изоморфна проективной специальной линейной группе $PSL(2, Z)$ , которая является фактором двумерной специальной линейной группы $SL(2, Z)$ по целым числам по ее центру ${I, - I}$ . Другими словами, $PSL(2, Z)$ состоит из всех матриц

{\begin{pmatrix}a&b\\c&d\end{pmatrix}}

где $a$ , $b$ , $c$ , $d$ — целые числа, $ad - bc = 1$ , а пары матриц $A$ и $- A$ считаются идентичными. Групповая операция представляет собой обычное умножение матриц .

Некоторые авторы определяют модульную группу как $PSL(2, Z)$ , а другие определяют модульную группу как большую группу $SL(2, Z)$ .

Некоторые математические соотношения требуют рассмотрения группы $GL(2, Z)$ матриц с определителем плюс или минус единица. ( $SL(2, Z)$ — подгруппа этой группы.) Аналогично, $PGL(2, Z)$ — это факторгруппа $GL(2, Z)/{I, - I}$ . Матрица 2 × 2 с единичным определителем является симплектической матрицей и, следовательно, $SL(2, Z) = Sp(2, Z)$ , симплектической группой матриц 2 × 2 .

Поиск элементов [ править ]

Чтобы найти явную матрицу

${\begin{pmatrix}a&x\\b&y\end{pmatrix}}$

в $SL(2, Z)$ начните с двух взаимно простых целых чисел $a,b$ и решим определительное уравнение

$ay-bx=1.$

(Обратите внимание на определяющее уравнение сил $a,b$ быть взаимно простым, так как в противном случае существовал бы множитель $c>1$ такой, что $ca'=a$ , $cb'=b$ , следовательно

$c(a'y-b'x)=1$

не будет иметь целочисленных решений.) Например, если $a=7,{\text{ }}b=6$ тогда определяющее уравнение имеет вид

$7y-6x=1$

затем принимая $y=-5$ и $x=-6$ дает $-35-(-36)=1$ , следовательно

${\begin{pmatrix}7&-6\\6&-5\end{pmatrix}}$

является матрицей. Затем, используя проекцию, эти матрицы определяют элементы в $PSL(2, Z)$ .

Теоретико-числовые свойства [ править ]

Определитель единицы измерения

{\begin{pmatrix}a&b\\c&d\end{pmatrix}}

означает, что дроби _{$.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}а / б$} , _{$кондиционер, $} _{$CD $} , _{$b / d$} несократимы, то есть не имеют общих делителей (при условии, что знаменатели ненулевые, конечно). В более общем смысле, если $p / q$ – неприводимая дробь, то

{\frac {ap+bq}{cp+dq}}

также неприводима (опять же при условии, что знаменатель не равен нулю). Таким образом можно соединить любую пару несократимых дробей; то есть для любой пары $п / к$ и $р / с$ несократимых дробей, существуют элементы

{\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in \operatorname {SL} (2,\mathbb {Z} )

такой, что

r=ap+bq\quad {\mbox{ and }}\quad s=cp+dq.

Элементы модулярной группы обеспечивают симметрию на двумерной решетке . Пусть $ω 1$ и $ω 2$ — два комплексных числа , отношение которых не является вещественным. Тогда множество точек

\Lambda (\omega _{1},\omega _{2})=\{m\omega _{1}+n\omega _{2}:m,n\in \mathbb {Z} \}

представляет собой решётку параллелограммов на плоскости. Другая пара векторов $α 1$ и $α 2$ будет порождать точно такую же решетку тогда и только тогда, когда

{\begin{pmatrix}\alpha _{1}\\\alpha _{2}\end{pmatrix}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}{\begin{pmatrix}\omega _{1}\\\omega _{2}\end{pmatrix}}

для некоторой матрицы из $GL(2, Z)$ . Именно по этой причине двоякопериодические функции , такие как эллиптические функции , обладают модулярной групповой симметрией.

Действие модульной группы на рациональные числа легче всего понять, представив квадратную сетку с точкой сетки $(p, q),$ соответствующей дроби $п / к$ (см. сад Евклида ). Несократимая дробь — это та, которая видна из начала координат; действие модульной группы на дробь никогда не переводит видимую (несводимую) в скрытую (приводимую), и наоборот.

Обратите внимание, что любой член модульной группы отображает проективно расширенную действительную прямую взаимно однозначным образом и, более того, биективно отображает проективно расширенную рациональную линию (рациональные числа с бесконечностью) в себя, иррациональные числа в иррациональные числа, трансцендентные числа в трансцендентные числа, недействительные числа к недействительным числам, верхняя полуплоскость к верхней полуплоскости и так далее.

Если $p n -1 / q n -1$ и $p n / q n$ — две последовательные дроби цепной дроби , то матрица

{\begin{pmatrix}p_{n-1}&p_{n}\\q_{n-1}&q_{n}\end{pmatrix}}

принадлежит $GL(2, Z)$ . В частности, если $bc - ad = 1$ для натуральных чисел $a$ , $b$ , $c$ , $d$ с $a < b$ и $c < d$ , то $группа $ $c / d$ будут соседями в последовательности Фарея порядка $max(b, d)$ . Важные частные случаи сходящихся дробей непрерывных дробей включают числа Фибоначчи и решения уравнения Пелла . В обоих случаях числа можно расположить так, чтобы сформировать полугрупповое подмножество модульной группы.

Теоретико-групповые свойства [ править ]

Презентация [ править ]

Можно показать, что модульная группа порождается двумя преобразованиями

{\begin{aligned}S&:z\mapsto -{\frac {1}{z}}\\T&:z\mapsto z+1\end{aligned}}

так что каждый элемент в модулярной группе может быть представлен (неоднозначным образом) композицией степеней $S$ и $T$ . Геометрически $S$ представляет собой инверсию в единичном круге с последующим отражением относительно воображаемой оси, а $T$ представляет собой единичный сдвиг вправо.

Генераторы $S$ и $T$ подчиняются соотношениям $S 2 = 1$ и $(СТ) 3 = 1$ . Это можно показать ^[1] что это полный набор отношений, поэтому модульная группа имеет представление :

\Gamma \cong \left\langle S,T\mid S^{2}=I,\left(ST\right)^{3}=I\right\rangle

В этом представлении модулярная группа описывается как группа треугольников $вращения D(2, 3, \infty)$ нет отношения $(бесконечность, поскольку на T$ ), и, таким образом, она отображается на все группы треугольников $(2, 3, n)$ путем добавления отношения $T н = 1$ , что происходит, например, в конгруэнц-подгруппе $Γ(n)$ .

Используя генераторы $S$ и $ST$ вместо $S$ и $T$ , это показывает, что модулярная группа изоморфна свободному произведению циклических групп $C 2$ и $C 3$ :

\Gamma \cong C_{2}*C_{3}

Действие $T : z \mapsto z + 1$ на $H$
Действие $S : z \mapsto - 1 / з$ на $Н$

Группа кос [ править ]

Группа кос $B 3$ является универсальным центральным расширением модулярной группы, причем они располагаются в виде решеток внутри (топологической) универсальной накрывающей группы $SL 2 (R) \to PSL 2 (R)$ . модулярная группа изоморфна фактор -группе B3 $Далее, модулярная группа имеет тривиальный центр и, следовательно , по$ модулю ее центра ; группе внутренних автоморфизмов B $3 .$ эквивалентно

Группа кос $B3,$ в свою очередь, изоморфна группе узлов узла -трилистника .

Частные [ править ]

Факторы по конгруэнтным подгруппам представляют значительный интерес.

Другими важными факторами являются $группы треугольников (2, 3, n)$ , которые геометрически соответствуют спуску в цилиндр, факторизуя $x$ координату по модулю $n$ , как $T н знак равно (z \mapsto z + п)$ . $(2, 3, 5)$ — это группа икосаэдрической симметрии , а $(2, 3, 7)$ группа треугольников (и связанная с ней мозаика) — это покрытие для всех поверхностей Гурвица .

Представление в виде матричной группы [ править ]

Группа ${\text{SL}}_{2}(\mathbb {Z} )$ может быть сгенерировано двумя матрицами ^[2]

S={\begin{pmatrix}0&-1\\1&0\end{pmatrix}},{\text{ }}T={\begin{pmatrix}1&1\\0&1\end{pmatrix}}

с

S^{2}=-I_{2},{\text{ }}(ST)^{3}={\begin{pmatrix}0&-1\\1&1\end{pmatrix}}^{3}=-I_{2}

Проекция ${\text{SL}}_{2}(\mathbb {Z} )\to {\text{PSL}}_{2}(\mathbb {Z} )$ превращает эти матрицы в генераторы ${\text{PSL}}_{2}(\mathbb {Z} )$ , с отношениями, аналогичными групповому представлению.

гиперболической геометрией Связь с

Модульная группа важна, потому что она образует подгруппу группы изометрий гиперболической плоскости . Если мы рассмотрим верхней полуплоскости модель $H$ геометрии гиперболической плоскости, то группа всех , сохраняющие ориентацию, изометрии $H$ состоят из всех преобразований Мёбиуса вида

z\mapsto {\frac {az+b}{cz+d}}

где $a$ , $b$ , $c$ , $d$ — действительные числа . В терминах проективных координат группа $PSL(2, R)$ действует на верхней полуплоскости $H$ проективно:

[z,\ 1]{\begin{pmatrix}a&c\\b&d\end{pmatrix}}\,=\,[az+b,\ cz+d]\,\thicksim \,\left[{\frac {az+b}{cz+d}},\ 1\right].

Это действие является верным . Поскольку $PSL(2, Z)$ является подгруппой $PSL(2, R)$ , модулярная группа является подгруппой группы изометрий $H$ , сохраняющих ориентацию . ^[3]

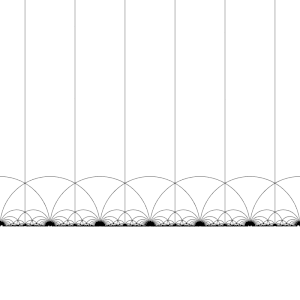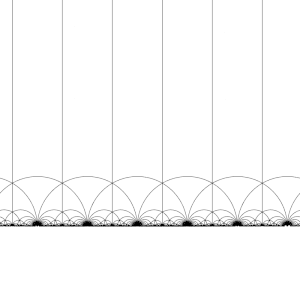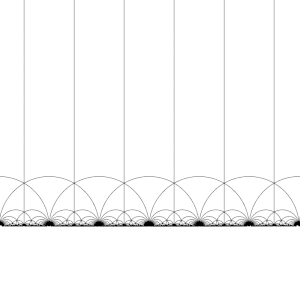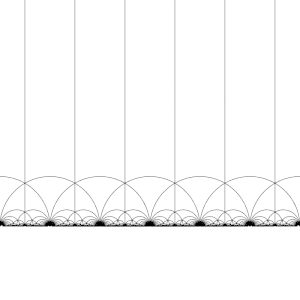
Тесселяция гиперболической плоскости [ править ]

Типичная фундаментальная область действия $Γ$ в верхней полуплоскости.

Модульная группа $Γ$ действует на ${\textstyle \mathbb {H} }$ как дискретная подгруппа ${\textstyle \operatorname {PSL} (2,\mathbb {R} )}$ , то есть для каждого $z$ в ${\textstyle \mathbb {H} }$ мы можем найти окрестность $z$ которая не содержит никаких других элементов орбиты z $,$ . Это также означает, что мы можем построить области , которые (грубо) содержат ровно одного представителя орбиты каждого $z$ в $H.$ фундаментальные (Необходима осторожность на границе домена.)

Существует много способов создания фундаментального домена, но общим выбором является регион.

R=\left\{z\in \mathbb {H} \colon \left|z\right|>1,\,\left|\operatorname {Re} (z)\right|<{\tfrac {1}{2}}\right\}

ограниченный вертикальными линиями $Re(z) = 1/2 и Re$ ) $(z = - 1/2 круг$ и $| г | = 1$ . Эта область представляет собой гиперболический треугольник. Он имеет вершины в $1/2 + я \sqrt 3/2 и$ $- 1/2 + я \sqrt 3/2 равен,$ где угол между его сторонами $π / 3$ и третья вершина, находящаяся на бесконечности, где угол между ее сторонами равен 0.

Существует сильная связь между модульной группой и эллиптическими кривыми . Каждая точка $z$ в верхней полуплоскости дает эллиптическую кривую, а именно фактор $\mathbb {C}$ решеткой, порожденной 1 и $z$ . Две точки в верхней полуплоскости дают изоморфные эллиптические кривые тогда и только тогда, когда они связаны преобразованием в модулярной группе. Таким образом, фактор верхней полуплоскости по действию модулярной группы представляет собой так называемое пространство модулей эллиптических кривых: пространство, точки которого описывают классы изоморфизма эллиптических кривых. Это часто визуализируется как описанная выше фундаментальная область с определенными точками на ее границе.

Модульная группа и ее подгруппы также являются источником интересных мозаик гиперболической плоскости. Преобразуя эту фундаментальную область по очереди каждым из элементов модульной группы, регулярное замощение гиперболической плоскости конгруэнтными гиперболическими треугольниками, известное как V6.6.∞ треугольная мозаика бесконечного порядка создается . Обратите внимание, что каждый такой треугольник имеет одну вершину либо на бесконечности, либо на действительной оси $Im(z) = 0$ .

Это разбиение можно распространить на диск Пуанкаре , где каждый гиперболический треугольник имеет одну вершину на границе диска. Разбиение диска Пуанкаре естественным образом задается $J$ -инвариантом , который инвариантен относительно модулярной группы и достигает каждого комплексного числа один раз в каждом треугольнике этих областей.

Эту тесселяцию можно немного усовершенствовать, разделив каждую область на две половины (обычно окрашенные в черный и белый цвета), добавив карту, меняющую ориентацию; тогда цвета соответствуют ориентации домена. Добавление $(x, y) \mapsto (- x, y)$ и взятие правой половины области $R$ (где $Re(z) \geq 0$ ) дает обычную мозаику. Эта мозаика впервые появляется в печати ( Klein & 1878/79a ), ^[4] где это приписывается Ричарду Дедекинду со ссылкой на ( Дедекинд 1877 ). ^[4]^[5]

Карту групп $(2, 3, \infty) \to (2, 3, n)$ (от модульной группы к треугольной группе) можно визуализировать с помощью этого разбиения (что дает разбиение на модульной кривой), как показано в видео. справа.

Паракомпактные равномерные разбиения семейства [∞,3] v т Это
Symmetry: [∞,3], (*∞32)							[∞,3]⁺ (∞32)	[1⁺,∞,3] (*∞33)		[∞,3⁺] (3*∞)

		=	=	=				= or	= or	=

{∞,3}	t{∞,3}	r{∞,3}	t{3,∞}	{3,∞}	rr{∞,3}	tr{∞,3}	sr{∞,3}	h{∞,3}	h₂{∞,3}	s{3,∞}
Uniform duals


V∞³	V3.∞.∞	V(3.∞)²	V6.6.∞	V3^∞	V4.3.4.∞	V4.6.∞	V3.3.3.3.∞	V(3.∞)³		V3.3.3.3.3.∞

Подгруппы конгруэнтности [ править ]

Важные подгруппы модулярной группы $Γ$ , называемые подгруппами конгруэнции , задаются путем наложения отношений конгруэнции на соответствующие матрицы.

Существует естественный гомоморфизм $SL(2, Z) \to SL(2, Z / N Z)$ заданный сокращением элементов по модулю $N.$ , Это индуцирует гомоморфизм модулярной группы $PSL(2, Z) \to PSL(2, Z / N Z)$ . Ядро и этого гомоморфизма называется главной конгруэнц-подгруппой уровня $N$ обозначается $Γ(N)$ . У нас есть следующая короткая точная последовательность :

1\to \Gamma (N)\to \Gamma \to \operatorname {PSL} (2,\mathbb {Z} /N\mathbb {Z} )\to 1.

Являясь ядром гомоморфизма $Γ(N),$ является нормальной подгруппой модулярной группы $Γ$ . Группа $Γ(N)$ задается как множество всех модулярных преобразований

z\mapsto {\frac {az+b}{cz+d}}

для которого $a \equiv d \equiv \pm1 (mod N)$ и $b \equiv c \equiv 0 (mod N)$ .

Легко показать, что след матрицы, представляющей элемент $Γ(N),$ не может быть равен −1, 0 или 1, поэтому эти подгруппы являются группами без кручения . (Существуют и другие подгруппы без кручения.)

Главную конгруэнтную подгруппу уровня 2, $Γ(2)$ , также называют модулярной группой $Λ$ . Поскольку $PSL(2, Z /2 Z)$ изоморфна $S3 6.$ , $Λ$ является подгруппой индекса Группа $Λ$ состоит из всех модулярных преобразований, для которых $a$ и $d$ нечетны, а $b$ и $c$ четны.

Другое важное семейство конгруэнтных подгрупп - это модулярная группа $Γ 0 (N),$ определенная как набор всех модулярных преобразований, для которых $c \equiv 0 (mod N)$ , или, что то же самое, как подгруппа, матрицы которой становятся верхнетреугольными при сокращении по модулю $N$ . Обратите внимание, что $Γ(N)$ является подгруппой $Γ 0 (N)$ . Модульные кривые , связанные с этими группами, являются аспектом чудовищного самогона — для простого числа $p$ модульная кривая нормализатора имеет нулевой род тогда и только тогда, когда $p$ делит порядок группы монстров или, что то же самое, если $p$ является суперсингулярной группой. основной .

Диадический моноид [ править ]

Одним из важных подмножеств модульной группы является диадический моноид , который является моноидом всех строк формы $ST. к СТ м СТ н ...$ для натуральных чисел $k, m, n,...$ . Этот моноид естественным образом возникает при изучении фрактальных кривых и описывает самоподобия симметрию функции Кантора , функции вопросительного знака Минковского и снежинки Коха , каждая из которых является частным случаем общей кривой де Рама . Моноид также имеет линейные представления более высокой размерности; например, $представление N = 3$ можно понимать как описание самосимметрии кривой бланманже .

Карты тора [ править ]

Группа $GL(2, Z)$ — это линейные отображения, сохраняющие стандартную решетку $Z 2$ , $SL(2, Z)$ — сохраняющие ориентацию отображения, сохраняющие эту решетку; они спускаются к самогомеоморфизмам тора таким образом , (отображение SL на сохраняющие ориентацию отображения) и фактически изоморфно отображаются в (расширенную) группу классов отображений что каждый самогомеоморфизм тора изотопен тора, что означает , карта такой формы. Алгебраические свойства матрицы как элемента $GL(2, Z)$ соответствуют динамике индуцированного отображения тора.

Хедж-группы [ править ]

Модульную группу можно обобщить до групп Хекке , названных в честь Эриха Хекке , и определить следующим образом. ^[7]

Группа Гекке $H q$ с $q \geq 3$ — это дискретная группа, порожденная

{\begin{aligned}z&\mapsto -{\frac {1}{z}}\\z&\mapsto z+\lambda _{q},\end{aligned}}

где $λ q = 2 cos π / q$ . Для малых значений $q \geq 3$ имеем:

{\begin{aligned}\lambda _{3}&=1,\\\lambda _{4}&={\sqrt {2}},\\\lambda _{5}&={\frac {1+{\sqrt {5}}}{2}},\\\lambda _{6}&={\sqrt {3}},\\\lambda _{8}&={\sqrt {2+{\sqrt {2}}}}.\end{aligned}}

Модульная группа $Γ$ изоморфна $H 3$ , и они имеют общие свойства и приложения – например, так же, как имеется свободное произведение циклических групп.

\Gamma \cong C_{2}*C_{3},

в более общем плане есть

H_{q}\cong C_{2}*C_{q},

что соответствует группе треугольников $(2, q, \infty)$ . Аналогично существует понятие главных конгруэнтных подгрупп, связанных с главными идеалами в $Z [λ]$ .

История [ править ]

Модульная группа и ее подгруппы были впервые подробно изучены Рихардом Дедекиндом и Феликсом Кляйном в рамках его программы в Эрлангене в 1870-х годах. Однако близкородственные эллиптические функции были изучены Жозефом Луи Лагранжем в 1785 году, а дальнейшие результаты по эллиптическим функциям были опубликованы Карлом Густавом Якобом Якоби и Нильсом Хенриком Абелем в 1827 году.

См. также [ править ]

Ссылки [ править ]

^ Альперин, Роджер К. (апрель 1993 г.). " $ПСЛ 2 (Z) = Z 2 * Z 3$ ". амер. Математика. Ежемесячно . 100 (4): 385–386. дои : 10.2307/2324963 . JSTOR 2324963 .
^ Конрад, Кейт. «SL(2,Z)» (PDF) .
^ МакКрири, Пол Р.; Мерфи, Тери Джо; Картер, Кристиан. «Модульная группа» (PDF) . Журнал Математика . 9 (3).
^ Перейти обратно: ^а ^б Ле Брюн, Ливен (22 апреля 2008 г.), Дедекинд или Кляйн?
^ Стиллвелл, Джон (январь 2001 г.). «Модульные чудеса». Американский математический ежемесячник . 108 (1): 70–76. дои : 10.2307/2695682 . ISSN 0002-9890 . JSTOR 2695682 .
^ Вестендорп, Джерард. «Платоновые мозаики римановых поверхностей» . www.xs4all.nl .
^ Розенбергер, Герхард; Хорошо, Бенджамин; Гальоне, Энтони М.; Спеллман, Деннис (2006). Комбинаторная теория групп, дискретные группы и теория чисел . п. 65. ИСБН 9780821839850 .

Апостол, Том М. (1990). Модульные функции и ряды Дирихле в теории чисел (2-е изд.). Нью-Йорк: Спрингер. гл. 2. ISBN 0-387-97127-0 .
Кляйн, Феликс (1878–1879), «О преобразовании эллиптических функций и решении уравнений пятой степени (О преобразовании эллиптических функций и ...)» , Math. 14 : 13–75, doi : 10.1007 /BF02297507 , S2CID 121056952 , заархивировано из оригинала 19 июля 2011 г. , получено 3 июня 2010 г.
Дедекинд, Ричард (сентябрь 1877 г.), «Письмо г-ну Борхардту о теории эллиптических модульных функций», Crelle's Journal , 83 : 265–292 .

[1] Альперин, Роджер К. (апрель 1993 г.). " $ПСЛ 2 (Z) = Z 2 * Z 3$ ". амер. Математика. Ежемесячно . 100 (4): 385–386. дои : 10.2307/2324963 . JSTOR 2324963 .

[2] Конрад, Кейт. «SL(2,Z)» (PDF) .

[3] МакКрири, Пол Р.; Мерфи, Тери Джо; Картер, Кристиан. «Модульная группа» (PDF) . Журнал Математика . 9 (3).

[lebruyn-4] Перейти обратно: ^а ^б Ле Брюн, Ливен (22 апреля 2008 г.), Дедекинд или Кляйн?

[5] Стиллвелл, Джон (январь 2001 г.). «Модульные чудеса». Американский математический ежемесячник . 108 (1): 70–76. дои : 10.2307/2695682 . ISSN 0002-9890 . JSTOR 2695682 .

[westendorp-6] Вестендорп, Джерард. «Платоновые мозаики римановых поверхностей» . www.xs4all.nl .

[7] Розенбергер, Герхард; Хорошо, Бенджамин; Гальоне, Энтони М.; Спеллман, Деннис (2006). Комбинаторная теория групп, дискретные группы и теория чисел . п. 65. ИСБН 9780821839850 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]