Треугольная группа

Эта статья о геометрической концепции. Информацию о Weihai, китайской компании по производству шин, см. в Triangle Group .

В математике группа треугольников — это группа , которую можно реализовать геометрически посредством последовательностей отражений по сторонам треугольника . Треугольник может быть обычным евклидовым треугольником, треугольником на сфере или гиперболическим треугольником . Каждая группа треугольников представляет собой группу симметрии евклидовой мозаики плоскости , сферы или гиперболической плоскости конгруэнтными треугольниками , называемыми треугольниками Мёбиуса , каждый из которых является фундаментальной областью действия.

Определение

Пусть l , m , n — целые числа , большие или равные 2. Группа треугольников Δ( l , m , n ) — это группа движений евклидовой плоскости, двумерной сферы, вещественной проективной плоскости или гиперболической плоскости. плоскость, создаваемая отражениями в сторонах треугольника с углами π/ l , π/ m и π/ n (измеряется в радианах ). Результатом отражений от двух соседних сторон является поворот на угол, в два раза превышающий угол между этими сторонами: 2π/ l , 2π/ m и 2π/ n . Следовательно, если порождающие отражения обозначены a , b , c и углы между ними в циклическом порядке такие, как указано выше, то выполняются следующие соотношения:

1. $a^{2}=b^{2}=c^{2}=1$
2. $(ab)^{l}=(bc)^{n}=(ca)^{m}=1.$

Это теорема о том, что все остальные отношения между a, b, c являются следствиями этих отношений и что ∆( l,m,n ) — дискретная группа движений соответствующего пространства. Таким образом, группа треугольников является группой отражения , допускающей групповое представление.

$\Delta (l,m,n)=\langle a,b,c\mid a^{2}=b^{2}=c^{2}=(ab)^{l}=(bc)^{n}=(ca)^{m}=1\rangle .$

Абстрактная группа в этом представлении представляет собой группу Кокстера с тремя образующими.

Классификация

Для любых натуральных чисел l , m , n > 1 ровно одна из классических двумерных геометрий (евклидова, сферическая или гиперболическая) допускает треугольник с углами (π/l, π/m, π/n), а пространство выложено отражениями треугольника. Сумма углов треугольника определяет тип геометрии по теореме Гаусса-Бонне : она евклидова, если сумма углов равна точно π, сферическая, если она превышает π, и гиперболическая, если она строго меньше π. При этом любые два треугольника с данными углами равны. Каждая группа треугольников определяет мозаику, которая традиционно раскрашена в два цвета, так что любые две соседние плитки имеют противоположные цвета.

В терминах чисел l , m , n > 1 возможны следующие возможности.

Евклидов случай

${\frac {1}{l}}+{\frac {1}{m}}+{\frac {1}{n}}=1.$

Группа треугольников — это бесконечная группа симметрии определенной мозаики (или мозаики) евклидовой плоскости треугольниками, сумма углов которых равна π (или 180 °). С точностью до перестановок тройка ( l , m , n ) является одной из троек (2,3,6), (2,4,4), (3,3,3). Соответствующие группы треугольников являются экземплярами групп обоев .

(2,3,6)	(2,4,4)	(3,3,3)
разделенная пополам шестиугольная плитка	квадратная плитка Тетракис	треугольная плитка
Более подробные диаграммы с обозначением вершин и показом того, как работает отражение:

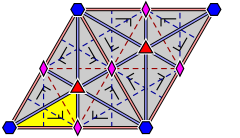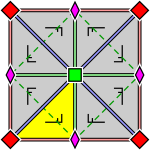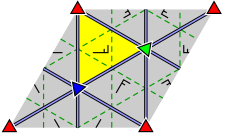Сферический корпус

${\frac {1}{l}}+{\frac {1}{m}}+{\frac {1}{n}}>1.$

Группа треугольников — это конечная группа симметрии мозаики единичной сферы сферическими треугольниками или треугольниками Мёбиуса , углы которых в сумме дают число, большее π. С точностью до перестановок тройка ( l , m , n ) имеет вид (2,3,3), (2,3,4), (2,3,5) или (2,2, n ), n > 1. Сферические группы треугольников можно отождествить с группами симметрии правильных многогранников в трехмерном евклидовом пространстве: ∆(2,3,3) соответствует тетраэдру , ∆(2,3,4) – как кубу , так и октаэдр так (который имеет одну и ту же группу симметрии), Δ(2,3,5) как додекаэдра , и икосаэдра . Группы Δ(2,2, n ), n > 1 двугранной симметрии можно интерпретировать как группы симметрии семейства диэдров , представляющих собой вырожденные твердые тела, образованные двумя одинаковыми правильными n -угольниками, соединенными вместе, или дуально осоэдрами , которые образуются путем соединения n двуугольников в двух вершинах.

Сферическая мозаика, соответствующая правильному многограннику, получается путем формирования барицентрического подразделения многогранника и проецирования полученных точек и линий на описанную сферу. В случае тетраэдра четыре грани, и каждая грань представляет собой равносторонний треугольник, разделенный на 6 меньших частей медианами, пересекающимися в центре. Полученная мозаика имеет 4×6=24 сферических треугольника (это сферический куб дисдякиса ).

Эти группы конечны, что соответствует компактности сферы – площади дисков в сфере вначале растут по радиусу, но со временем охватывают всю сферу.

Треугольные плитки изображены ниже:

(2,2,2)	(2,2,3)	(2,2,4)	(2,2,5)	(2,2,6)	(2,2,н)
(2,3,3)		(2,3,4)		(2,3,5)

Сферические мозаики, соответствующие октаэдру и икосаэдру, а также двугранные сферические мозаики с четным n симметричны центрально . Следовательно, каждый из них определяет замощение вещественной проективной плоскости — эллиптическое замощение . Ее группа симметрии представляет собой фактор группы сферического треугольника по отражению через начало координат (-I ) , которое является центральным элементом порядка 2. Поскольку проективная плоскость является моделью эллиптической геометрии , такие группы называются группами эллиптических треугольников.

Гиперболический случай

${\frac {1}{l}}+{\frac {1}{m}}+{\frac {1}{n}}<1.$

Группа треугольников — это бесконечная группа симметрии замощения гиперболической плоскости гиперболическими треугольниками, сумма углов которых дает число меньше π. Все тройки, еще не перечисленные, представляют собой мозаику гиперболической плоскости. Например, тройка (2,3,7) образует группу треугольников (2,3,7) . Таких групп бесконечно много; мозаики, связанные с некоторыми небольшими значениями:

Гиперболическая плоскость

Модель диска Пуанкаре фундаментальных треугольников доменов

Пример прямоугольных треугольников (2 шт.)
(2 3 7)	(2 3 8)	(2 3 9)	(2 3 ∞)
(2 4 5)	(2 4 6)	(2 4 7)	(2 4 8)	(2 4 ∞)
(2 5 5)	(2 5 6)	(2 5 7)	(2 6 6)	(2 ∞ ∞)
Пример обычных треугольников (pqr)
(3 3 4)	(3 3 5)	(3 3 6)	(3 3 7)	(3 3 ∞)
(3 4 4)	(3 6 6)	(3 ∞ ∞)	(6 6 6)	(∞ ∞ ∞)

Гиперболические треугольные группы являются примерами неевклидовых кристаллографических групп и были обобщены в теории Громова гиперболических групп .

Из групп Дайка

Обозначим через D ( l , m , n ) подгруппу индекса , 2 в ∆(l,m,n) порожденную словами четной длины в образующих. Такие подгруппы иногда называют «обычными» треугольными группами. или группы фон Дейка , в честь Вальтера фон Дейка . Для сферических, евклидовых и гиперболических треугольников они соответствуют элементам группы, сохраняющей ориентацию треугольника, – группе вращений. Для проективных (эллиптических) треугольников их нельзя интерпретировать так, поскольку проективная плоскость неориентируема, поэтому не существует понятия «сохранение ориентации». Однако отражения локально меняют ориентацию (и каждое многообразие локально ориентируемо, поскольку локально евклидово): они фиксируют линию, и в каждой точке линии есть отражение поперек этой линии.

Группа D ( l , m , n ) определяется следующим представлением:

$D(l,m,n)=\langle x,y\mid x^{l},y^{m},(xy)^{n}\rangle .$

С точки зрения генераторов, приведенных выше, это x = ab, y = ca, yx = cb . Геометрически три элемента x , y , xy соответствуют поворотам на 2π/ l , 2π/ m и 2π/ n вокруг трех вершин треугольника.

Обратите внимание, что D ( l , m , n ) ≅ D ( m , l , n ) ≅ D ( n , m , l ), ​​поэтому D ( l , m , n ) не зависит от порядка l , m , n .

Гиперболическая группа фон Дейка — это фуксова группа , дискретная группа, состоящая из сохраняющих ориентацию изометрий гиперболической плоскости.

Перекрывающиеся плитки

Дополнительная информация: треугольник Шварца.

Группы треугольников сохраняют мозаику из треугольников, а именно фундаментальную область действия (треугольник, определяемый линиями отражения), называемую треугольником Мёбиуса , и задаются тройкой целых чисел ( l , m , n ), – целые числа соответствуют (2l , 2m , 2n ) треугольникам, сходящимся в вершине. Существуют также замощения перекрывающимися треугольниками, которые соответствуют треугольникам Шварца с рациональными числами ( l / a , m / b , n / c ), где знаменатели взаимно просты с числителями. Это соответствует ребрам, встречающимся под углами a π/ l (соответственно), что соответствует повороту 2 a π/ l (соответственно), который имеет порядок l и, таким образом, идентичен как элемент абстрактной группы, но отличен, когда представлено отражением.

Например, треугольник Шварца (2 3 3) дает замощение . сферы плотностью 1, а треугольник (2 3/2 3) дает замощение сферы плотностью 3, но с той же абстрактной группой Эти симметрии перекрывающихся мозаик не считаются группами треугольников.

История

Группы треугольников датируются, по крайней мере, представлением икосаэдрической группы как (вращательной) (2,3,5) группы треугольников Уильямом Роуэном Гамильтоном в 1856 году в его статье об икосианском исчислении .

Приложения

Внешние видео
Деформированная модульная плитка – визуализация карты (2,3,∞) → (2,3,7) путем морфинга связанных мозаик.

Группы треугольников возникают в арифметической геометрии . Модульная группа порождается двумя элементами, S и T , подчиняющимися отношениям S² = ( ST )³ = 1 (нет связи с T ), является группой вращательного треугольника (2,3,∞) и отображается на все треугольники группы (2,3, n ), добавив отношение T ^н = 1. В более общем смысле, группа Гекке H _q порождается двумя элементами, S и T , подчиняющимися соотношениям S ² = ( СТ ) ^д = 1 (нет отношения к T ), является группой треугольников вращения (2, q , ∞) и отображается на все группы треугольников (2, q , n ), добавляя отношение T ^н = 1 модулярная группа является группой Гекке H ₃ . В Гротендика теории детских рисунков функция Белого приводит к мозаике римановой поверхности областями отражения группы треугольников.

Все 26 спорадических групп являются факторами групп треугольников. из которых 12 являются группами Гурвица (факторы группы (2,3,7)).

См. также

• Треугольник Шварца
• Карта треугольника Шварца — это карта треугольников на верхнюю полуплоскость .
• Геометрическая теория групп

Ссылки

• Магнус, Вильгельм (1974), «II. Разрывные группы и треугольные мозаики», Неевклидовы мозаики и их группы , Academic Press , стр. 52–106 , ISBN  978-0-12-465450-1
• Гросс, Джонатан Л.; Такер, Томас В. (2001), «6.2.8 Группы треугольников», Топологическая теория графов , Courier Dover Publications, стр. 279–281 , ISBN  978-0-486-41741-7
• Уилсон, Р.А. (2001), «Монстр - это группа Гурвица» , Журнал теории групп , 4 (4): 367–374, номер документа : 10.1515/jgth.2001.027 , MR   1859175 , заархивировано из оригинала 03.03.2012 г. 05 , получено 4 сентября 2015 г.

Внешние ссылки

• Элизабет Р Чен треугольник группы (2010) фоновые изображения для рабочего стола

Эта статья включает в себя материалы групп Triangle на PlanetMath , которые доступны под лицензией Creative Commons Attribution/Share-Alike License .