Достаточно
| Достаточно регулярно | |
|---|---|
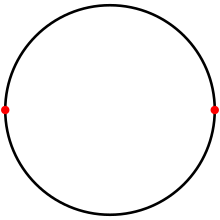 На круге двуугольник представляет собой мозаику с двумя противоположными точками и двумя дугами по 180°. | |
| Тип | Правильный многоугольник |
| Ребра и вершины | 2 |
| Символ Шлефли | {2} |
| Диаграммы Кокстера – Дынкина | |
| Группа симметрии | Д 2 , [2], (*2•) |
| Двойной полигон | Самодвойственный |
В геометрии двуугольник ребрами или 2- угольник — это многоугольник с двумя сторонами ( ) и двумя вершинами . Его конструкция вырождена в евклидовой плоскости , потому что либо две стороны совпадут, либо одна или обе должны быть искривлены; однако его можно легко визуализировать в эллиптическом пространстве. Его также можно рассматривать как представление графа с двумя вершинами, см. « Обобщенный многоугольник ».
Правильный двуугольник имеет равные оба угла и обе стороны и обозначается символом Шлефли {2}. Его можно построить на сфере в виде пары дуг по 180 градусов, соединяющих противоположные точки , когда он образует луну .
Дигон — простейший абстрактный многогранник ранга 2.
двуугольник Усеченный t {2} является квадратом {4}. Перемеженный двуугольник h {2} является моногоном {1}.
В евклидовой геометрии [ править ]
Дигон может иметь одно из двух визуальных представлений, если его поместить в евклидово пространство.
Одно представление является вырожденным и визуально выглядит как двойное накрытие отрезка прямой . Появляясь, когда минимальное расстояние между двумя краями равно 0, эта форма возникает в нескольких ситуациях. Эта форма двойного покрытия иногда используется для определения вырожденных случаев некоторых других многогранников; например, правильный тетраэдр можно рассматривать как антипризму, образованную таким двуугольником. Его можно получить путем чередования квадрата (h{4}), поскольку для этого требуется соединить две противоположные вершины этого квадрата. Когда чередуются многогранники более высокой размерности, включающие квадраты или другие тетрагональные фигуры, эти двуугольники обычно отбрасываются и считаются одиночными ребрами.
Второе визуальное представление, бесконечное по размеру, представляет собой две параллельные линии, простирающиеся до бесконечности (и проективно встречающиеся в ней, т. е. имеющие вершины) и возникающие, когда кратчайшее расстояние между двумя краями больше нуля. Эта форма возникает при представлении некоторых вырожденных многогранников, ярким примером является апейрогональный осоэдр , предел общего сферического осоэдра на бесконечности, состоящий из бесконечного числа двуугольников, встречающихся в двух противоположных точках на бесконечности. [1] Однако, поскольку вершины этих двуугольников находятся на бесконечности и, следовательно, не связаны замкнутыми отрезками прямых, эта мозаика обычно не считается дополнительной регулярной мозаикой евклидовой плоскости, даже когда ее двойное апейрогональное замощение второго порядка (бесконечный диэдр ) является.
- Соединение двух двуугольников «отрезков прямой» как двух возможных чередований квадрата (обратите внимание на расположение вершин ).
- Апейрогональный осоэдр , содержащий бесконечно узкие двуугольники.
Любой прямосторонний двуугольник является правильным, даже если он вырожден, поскольку его два ребра имеют одинаковую длину и два угла равны (оба равны нулю градусов). Таким образом, правильный двуугольник является конструктивным многоугольником . [2]
Некоторые определения многоугольника не считают двуугольник правильным многоугольником из-за его вырождения в евклидовом случае. [3]
В элементарных многогранниках [ править ]

Двуугольник как грань многогранника поскольку является вырожденным, он является вырожденным многоугольником. Но иногда он может иметь полезное топологическое существование при преобразовании многогранников.
Как сферическая луна [ править ]
Сферическая луна — это двуугольник, две вершины которого являются противоположными точками на сфере. [4]
Сферический многогранник, построенный из таких двуугольников, называется осоэдром .
- Луна на сфере.
- Шесть двуугольных граней правильного шестиугольного осоэдра .
значимость Теоретическая
Этот раздел может потребовать очистки Википедии , чтобы соответствовать стандартам качества . Конкретная проблема заключается в следующем: не хватает цитат или вики-ссылок, которые, вероятно, тоже можно было бы лучше объяснить. ( сентябрь 2015 г. ) |

Двуугольник — важная конструкция в топологической теории сетей, таких как графы и многогранные поверхности. Топологическая эквивалентность может быть установлена с использованием процесса сведения к минимальному набору многоугольников, не затрагивая глобальные топологические характеристики, такие как значение Эйлера. Двуугольник представляет собой этап упрощения, на котором его можно просто удалить и заменить отрезком прямой, не влияя на общие характеристики.
Циклические группы могут быть получены как симметрии вращения многоугольников: симметрия вращения двуугольника дает группу C 2 .
Дигоны (бигоны) могут использоваться при построении и анализе различных топологических структур. [5] такие как структуры заболеваемости .
См. также [ править ]
Ссылки [ править ]
Цитаты [ править ]
- ^ Симметрии вещей 2008, Джон Х. Конвей, Хайди Бургель, Хаим Гудман-Штраус, ISBN 978-1-56881-220-5 , с. 263
- ^ Эрик Т. Экхофф; Построение правильных многоугольников. Архивировано 14 июля 2015 г. в Wayback Machine , Университет штата Айова. (получено 20 декабря 2015 г.)
- ^ Коксетер (1973), Глава 1, Многоугольники и многогранники , стр.4
- ^ Коксетер (1973), Глава 1, Многоугольники и многогранники , страницы 4 и 12.
- ↑ Перейти обратно: Перейти обратно: а б Алекс Дегтярев, Топология алгебраических кривых: подход через Dessins d'Enfants , с. 262
Библиография [ править ]
- Герберт Буземан , Геометрия геодезических. Нью-Йорк, Академик Пресс, 1955 г.
- Коксетер , Правильные многогранники (третье издание), Dover Publications Inc, 1973 г. ISBN 0-486-61480-8
- Вайсштейн, Эрик В. «Дигон» . Математический мир .
- А.Б. Иванов (2001) [1994], «Дигон» , Энциклопедия Математики , EMS Press
Внешние ссылки [ править ]
 СМИ, связанные с дигонами, на Викискладе?
СМИ, связанные с дигонами, на Викискладе?