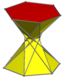
Антипризма

Набор однородных $n$ -угольных антипризм
Набор однородных n -угольных антипризм
	Однородная шестиугольная антипризма ( n = 6 )
Тип	однородный в смысле полуправильный многогранник
Лица	2 правильных n -угольника ; 2 n равносторонних треугольников
Края	4 н
Вершины	22н
Конфигурация вершин	3.3.3. н
Символ Шлефли	{ }⊗{ п } ; с{ 2,2n } ; ср{2, п }
Обозначение Конвея	н
Диаграмма Кокстера	;
Группа симметрии	Д н д , [2 + ,2 n ], (2* n ) , порядок 4 n
Группа вращения	Д н , [2, н ] + , (22 n ) , порядок 2 n
Двойной многогранник	выпуклый дуально-однородный n -угольный трапецоэдр
Характеристики	выпуклые , вершинно-транзитивные , правильные многоугольные грани, конгруэнтные и коаксиальные основания
Сеть
	Сеть одноугольных эннеагональных антипризм ( n = 9 )

В геометрии n $антипризма$ -угольная или n $-$ антипризма — это многогранник , составленный из двух параллельных прямых копий (не зеркальных изображений) $n$ -стороннего многоугольника , соединенных чередующейся полосой из $2 n$ треугольников . представлены обозначением Конвея $An .$ Они

Антипризмы — подкласс призматоидов и представляют собой (вырожденный) тип курносого многогранника .

Антипризмы подобны призмам что основания закручены относительно друг друга, а боковые грани (соединяющие основания) представляют собой $2n, за исключением того ,$ треугольников, а не $n$ четырёхугольников .

Двойственный многогранник n $- угольной$ антипризмы является $n$ -угольным трапецоэдром .

История [ править ]

В своей книге «Harmonices Mundi» 1619 года Иоганн Кеплер наблюдал существование бесконечного семейства антипризм. ^[2] Обычно это считается первым открытием этих форм, но, возможно, они были известны раньше: неподписанный печатный блок для сетки шестиугольной антипризмы был приписан Иерониму Андрее , который умер в 1556 году. ^[3]

Немецкая форма слова «антипризма» использовалась для обозначения этих форм в 19 веке; Карл Хайнце приписывает свое введение Теодору Витштейну [ де ] . ^[4] Хотя английское слово «антипризма» ранее использовалось для обозначения оптической призмы, используемой для подавления эффектов первичного оптимального элемента, ^[5] Первое использование слова «антипризма» в английском языке в его геометрическом смысле, по-видимому, относится к началу 20 века в работах HSM Coxeter . ^[6]

Особые случаи [ править ]

Правая антипризма [ править ]

Для антипризмы с правильными $основаниями n$ -угольников обычно рассматривают случай, когда эти две копии закручены на угол $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}180 / н$ градусов.

Ось перпендикулярная правильного многоугольника — это линия, плоскости многоугольника и лежащая в центре многоугольника.

Для антипризмы с равными правильными основаниями $n$ -угольников, закрученной на угол $180 / n$ градусов, большая регулярность получается, если основания имеют одну и ту же ось: соосны ; т.е. (для некомпланарных оснований): если линия, соединяющая центры оснований, перпендикулярна плоскостям основания. Тогда антипризма называется прямой антипризмой , а ее $2n боковых$ граней — равнобедренными треугольниками .

Равномерная антипризма [ править ]

Однородная треугольников в $n$ -антипризма имеет два конгруэнтных правильных $n$ -угольника в качестве основных граней и $2 n$ равносторонних качестве боковых граней.

Однородные антипризмы, как и однородные призмы, образуют бесконечный класс вершинно-транзитивных многогранников. При $n = 2$ имеем двуугольную антипризму (вырожденную антипризму), визуально идентичную правильному тетраэдру ; для $n = 3$ правильный октаэдр как треугольная антипризма (невырожденная антипризма).

Семейство однородных n -угольных антипризм
v
т
Это
Название антипризмы	Дигональная антипризма	(Треугольный) Треугольная антипризма	(Тетрагональный) Квадратная антипризма	Пятиугольная антипризма	Шестиугольная антипризма	Семиугольная антипризма	...	Апейрогональная антипризма
Изображение многогранника							...
Сферическое мозаичное изображение							Плоское мозаичное изображение
Конфигурация вершины.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	...	∞.3.3.3

Диаграммы Шлегеля этих полуправильных антипризм имеют следующий вид:

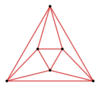А3	A4	А5	А6	A7	А8

Декартовы координаты [ править ]

Декартовы координаты вершин прямой n $-$ антипризмы (т.е. с правильными $n$ основаниями $-угольников и 2n боковыми гранями$ равнобедренного треугольника):

\left(\cos {\frac {k\pi }{n}},\sin {\frac {k\pi }{n}},(-1)^{k}h\right)

где $0 \leq k \leq 2 n - 1$ ;

если $n$ -антипризма однородна (т.е. если треугольники равносторонние), то:

2h^{2}=\cos {\frac {\pi }{n}}-\cos {\frac {2\pi }{n}}.

Объем и площадь поверхности [ править ]

Пусть $a$ — длина ребра однородной n $-$ угольной антипризмы; тогда объем:

V={\frac {n{\sqrt {4\cos ^{2}{\frac {\pi }{2n}}-1}}\sin {\frac {3\pi }{2n}}}{12\sin ^{2}{\frac {\pi }{n}}}}~a^{3},

а площадь поверхности равна:

A={\frac {n}{2}}\left(\cot {\frac {\pi }{n}}+{\sqrt {3}}\right)a^{2}.

Кроме того, объем правильной прямоугольной n $-$ угольной антипризмы с длиной стороны ее оснований $l$ и высотой $h$ определяется выражением:

V={\frac {nhl^{2}}{12}}\left(\csc {\frac {\pi }{n}}+2\cot {\frac {\pi }{n}}\right).

Заметим, что объем прямой $n$ -угольной призмы с одинаковыми $l$ и $h$ равен:

V_{\mathrm {prism} }={\frac {nhl^{2}}{4}}\cot {\frac {\pi }{n}}

что меньше, чем у антипризмы.

Симметрия [ править ]

правой Группа симметрии n = $-антипризмы$ (т.е. с правильными основаниями и равнобедренными боковыми гранями) равна $D n d D n v$ порядка $4 n$ , за исключением случаев:

$n = 2$ : правильный тетраэдр , который имеет большую группу симметрии $T d$ порядка $24 = 3 \times (4 \times 2)$ , которая имеет три версии $D 2d$ в качестве подгрупп;

$n = 3$ : правильный октаэдр , который имеет большую группу симметрии $Oh порядка$ . $48 = 4 \times (4 \times 3)$ и имеет четыре версии $D 3d$ в качестве подгрупп

Группа симметрии содержит инверсию тогда и только тогда, когда $n$ нечетно.

представляет Группа вращения собой $D n$ порядка $2 n$ , за исключением случаев:

$n = 2$ : правильный тетраэдр, который имеет большую группу вращения $T$ порядка $12 = 3 \times (2 \times 2)$ , которая имеет три версии $D 2$ в качестве подгрупп;

$n = 3$ : правильный октаэдр, который имеет большую группу вращения $O$ порядка $24 = 4 \times (2 \times 3)$ , которая имеет четыре версии $D 3$ в качестве подгрупп.

Примечание. Правые $n$ -антипризмы имеют конгруэнтные основания правильных $n$ -угольников и конгруэнтные боковые грани равнобедренного треугольника, поэтому имеют ту же (двугранную) группу симметрии, что и равномерная $n$ -антипризма, для $n \geq 4$ .

Обобщения [ править ]

В высших измерениях [ править ]

Четырехмерные антипризмы можно определить как имеющие два двойственных многогранника как параллельные противоположные грани, так что каждая трехмерная грань между ними происходит из двух двойственных частей многогранников: вершины и двойного многоугольника или двух двойных ребер. Каждый трехмерный выпуклый многогранник комбинаторно эквивалентен одной из двух противоположных граней четырехмерной антипризмы, построенной из его канонического многогранника и его двойственного полярного многогранника. ^[7] Однако существуют четырехмерные многогранники, которые нельзя объединить со своими двойниками в пятимерные антипризмы. ^[8]

Самопересекающиеся многогранники [ править ]

5/2-антипризма		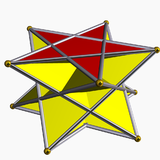	5/3-антипризма
9/2-антипризма		9/4-антипризма		9/5-антипризма

Здесь показаны все незвездные и звездные антипризмы до 15 сторон, включая стороны 29-угольника.

Однородные звездные антипризмы названы по звездчатых многоугольников основаниям ${p / q}$ и существуют в прямом и ретроградном (перекрещенных) решениях. Скрещенные формы имеют пересекающиеся фигуры вершин и обозначаются «перевернутыми» дробями: $p /(p - q)$ вместо $p / q$ ; пример: 5/3 вместо 5/2.

Правая звездчатая антипризма имеет две конгруэнтные коаксиальные базовые грани правильного выпуклого или звездчатого многоугольника и $2 n$ равнобедренного треугольника боковых граней .

Любую звездную антипризму с правильным выпуклым или звездчатым многоугольным основанием можно сделать правильной звездной антипризмой (при необходимости переместив и/или повернув одно из ее оснований).

В ретроградных формах, но не в прямоходных, треугольники, соединяющие выпуклые или звездчатые основания, пересекают ось вращательной симметрии. Таким образом:

Ретроградные звездные антипризмы с основаниями правильных выпуклых многоугольников не могут иметь равные длины ребер и поэтому не могут быть однородными. «Исключение»: антипризма ретроградной звезды с основаниями равностороннего треугольника (конфигурация вершин: 3.3/2.3.3) может быть однородной; но тогда он имеет вид равностороннего треугольника: это вырожденный звездчатый многогранник.

Точно так же некоторые ретроградные звездные антипризмы с основаниями правильных звездчатых многоугольников не могут иметь равные длины ребер и поэтому не могут быть одинаковыми. Пример: антипризма ретроградной звезды с основаниями обычной звезды 7/5 (конфигурация вершин: 3.3.3.7/5) не может быть однородной.

Также $p / q$ можно построить соединения звездных антипризм с правильными звездчатыми основаниями $-угольников, если p$ и $q$ имеют общие множители. Пример: звезда 10/4-антипризма представляет собой соединение двух звезд 5/2-антипризмы.

Звездчатые $p / q$ -антипризмы по симметрии, для $p \leq 12$
Symmetry group	Uniform stars			Right stars
$D 4d [2 +,8] (2*4)$				3.3/2.3.4 Crossed square antiprism
$D 5h [2,5] (*225)$	3.3.3.5/2 Pentagrammic antiprism			3.3/2.3.5 crossed pentagonal antiprism
$D 5d [2 +,10] (2*5)$	3.3.3.5/3 Pentagrammic crossed-antiprism
$D 6d [2 +,12] (2*6)$				3.3/2.3.6 crossed hexagonal antiprism
$D 7h [2,7] (*227)$	3.3.3.7/2	3.3.3.7/4
$D 7d [2 +,14] (2*7)$	3.3.3.7/3
$D 8d [2 +,16] (2*8)$	3.3.3.8/3 Octagrammic antiprism	3.3.3.8/5 Octagrammic crossed-antiprism
$D 9h [2,9] (*229)$	3.3.3.9/2 Enneagrammic antiprism (9/2)	3.3.3.9/4 Enneagrammic antiprism (9/4)
$D 9d [2 +,18] (2*9)$	3.3.3.9/5 Enneagrammic crossed-antiprism
$D 10d [2 +,20] (2*10)$	3.3.3.10/3 Decagrammic antiprism
$D 11h [2,11] (*2.2.11)$	3.3.3.11/2	3.3.3.11/4	3.3.3.11/6
$D 11d [2 +,22] (2*11)$	3.3.3.11/3	3.3.3.11/5	3.3.3.11/7
$D 12d [2 +,24] (2*12)$	3.3.3.12/5	3.3.3.12/7
...	...

См. также [ править ]

Большая антипризма , четырёхмерный многогранник.
Косой многоугольник — трехмерный многоугольник, выпуклая оболочка которого представляет собой антипризму.

Ссылки [ править ]

^ Н. В. Джонсон : Геометрии и трансформации , (2018) ISBN 978-1-107-10340-5 Глава 11: Конечные группы симметрии , 11.3 Пирамиды, призмы и антипризмы, рисунок 11.3c
^ Кеплер, Иоганн (1619). «Книга II, Определение X» . Harmonices Mundi (на латыни). п. 49. См. также иллюстрацию А семиугольной антипризмы.
^ Шрайбер, Питер; Фишер, Гизела ; Стернат, Мария Луиза (июль 2008 г.). «Новый взгляд на повторное открытие архимедовых тел в эпоху Возрождения». Архив истории точных наук . 62 (4): 457–467. JSTOR 41134285 .
^ Хайнце, Карл (1886). Лаке, Франц (ред.). Генетическая стереометрия (на немецком языке). Б. Г. Тойбнер. п. 14.
^ Смит, Пьяцци (1881). «XVII. О строении линий, образующих низкотемпературный спектр кислорода». Труды Королевского общества Эдинбурга . 30 (1): 419–425. дои : 10.1017/s0080456800029112 .
^ Коксетер, HSM (январь 1928 г.). «Чистые архимедовы многогранники в шести и семи измерениях». Математические труды Кембриджского философского общества . 24 (1): 1–9. дои : 10.1017/s0305004100011786 .
^ Грюнбаум, Бранко (2005). «Действительно ли скучны призмы и антипризмы? (Часть 3)» (PDF) . Геомбинаторика . 15 (2): 69–78. МР 2298896 .
^ Доббинс, Майкл Джин (2017). «Антипризменность, или: сведение комбинаторной эквивалентности к проективной эквивалентности в задачах реализуемости многогранников». Дискретная и вычислительная геометрия . 57 (4): 966–984. дои : 10.1007/s00454-017-9874-y . МР 3639611 .

Дальнейшее чтение [ править ]

Энтони Пью (1976). Многогранники: визуальный подход . Калифорния: Издательство Калифорнийского университета в Беркли. ISBN 0-520-03056-7 . Глава 2: Архимедовы многогранники, призмы и антипризмы

Внешние ссылки [ править ]

СМИ, связанные с антипризмами, на Викискладе?
Вайсштейн, Эрик В. «Антипризма» . Математический мир .
Невыпуклые призмы и антипризмы
Бумажные модели призм и антипризм.

[1] Н. В. Джонсон : Геометрии и трансформации , (2018) ISBN 978-1-107-10340-5 Глава 11: Конечные группы симметрии , 11.3 Пирамиды, призмы и антипризмы, рисунок 11.3c

[2] Кеплер, Иоганн (1619). «Книга II, Определение X» . Harmonices Mundi (на латыни). п. 49. См. также иллюстрацию А семиугольной антипризмы.

[3] Шрайбер, Питер; Фишер, Гизела ; Стернат, Мария Луиза (июль 2008 г.). «Новый взгляд на повторное открытие архимедовых тел в эпоху Возрождения». Архив истории точных наук . 62 (4): 457–467. JSTOR 41134285 .

[4] Хайнце, Карл (1886). Лаке, Франц (ред.). Генетическая стереометрия (на немецком языке). Б. Г. Тойбнер. п. 14.

[5] Смит, Пьяцци (1881). «XVII. О строении линий, образующих низкотемпературный спектр кислорода». Труды Королевского общества Эдинбурга . 30 (1): 419–425. дои : 10.1017/s0080456800029112 .

[6] Коксетер, HSM (январь 1928 г.). «Чистые архимедовы многогранники в шести и семи измерениях». Математические труды Кембриджского философского общества . 24 (1): 1–9. дои : 10.1017/s0305004100011786 .

[7] Грюнбаум, Бранко (2005). «Действительно ли скучны призмы и антипризмы? (Часть 3)» (PDF) . Геомбинаторика . 15 (2): 69–78. МР 2298896 .

[8] Доббинс, Майкл Джин (2017). «Антипризменность, или: сведение комбинаторной эквивалентности к проективной эквивалентности в задачах реализуемости многогранников». Дискретная и вычислительная геометрия . 57 (4): 966–984. дои : 10.1007/s00454-017-9874-y . МР 3639611 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]