Большая антипризма
| Большая антипризма | |
|---|---|
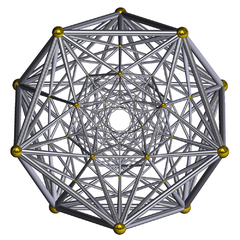 ( Каркасная диаграмма Шлегеля ) | |
| Тип | Равномерный 4-многогранник |
| Единый индекс | 47 |
| Клетки | 100+200 ( 3.3.3 ) 20 ( 3.3.3.5 ) |
| Лица | 20 {5} 700 {3} |
| Края | 500 |
| Вершины | 100 |
| Вершинная фигура | Сфенокорона  |
| Группа симметрии | Ионная уменьшенная группа Кокстера [[10,2 + ,10]] порядка 400 |
| Характеристики | выпуклый |
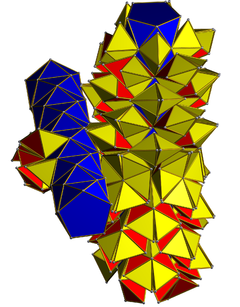 Сеть , показывающая два непересекающихся кольца из 10 антипризм. 200 тетраэдров (желтые) контактируют гранями с антипризмами, а 100 тетраэдров (красные) контактируют только с другими тетраэдрами. | |
В геометрии большая антипризма или пятиугольная двойная антипризма — это однородный 4-мерный многогранник (4-мерный однородный многогранник ), ограниченный 320 ячейками : 20 пятиугольными антипризмами и 300 тетраэдрами . Это аномальный, не витоффов однородный 4-многогранник, открытый в 1965 году Конвеем и Гаем . [1] [2] Топологически, при своей высшей симметрии, пятиугольные антипризмы имеют симметрию D 5d и существуют два типа тетраэдров: один с симметрией S 4 и один с симметрией C s .
Альтернативные названия
[ редактировать ]- Пятиугольный двойной антипризмоид Нормана В. Джонсона
- Гэп (Джонатан Бауэрс: за великую антипризму) [3]
Структура
[ редактировать ]20 сложенных друг на друга пятиугольных антипризм образуют два непересекающихся кольца по 10 антипризм в каждом. Антипризмы в каждом кольце соединены друг с другом пятиугольными гранями. Два кольца взаимно перпендикулярны и имеют структуру, похожую на дуопризму .
300 тетраэдров соединяют два кольца друг с другом и располагаются в двухмерном расположении, топологически эквивалентном 2-тору и ребру дуоцилиндра . Их можно разделить еще на три набора. 100 торцевых сопряжений с одним кольцом, 100 торцевых сопряжений с другим кольцом и 100 центров точно по центру дуоцилиндра и краевых сопряжений с обоими кольцами. Этот последний набор образует плоский тор и может быть «развернут» в плоский квадратный массив тетраэдров размером 10 × 10, которые встречаются только по краям и вершинам. См. рисунок ниже.

Кроме того, 300 тетраэдров можно разделить на 10 непересекающихся спиралей Бурдейка – Кокстера по 30 ячеек в каждой, которые замыкаются друг на друга. Две пятиугольные трубки антипризмы плюс 10 спиралей BC образуют нерегулярное дискретное расслоение Хопфа большой антипризмы, которое Хопф отображает на грани пятиугольной антипризмы. Две трубки соответствуют двум пятиугольным граням, а 10 спиралей BC соответствуют 10 треугольным граням.
Структура большой антипризмы аналогична структуре трехмерных антипризм . Однако большая антипризма — единственный выпуклый однородный аналог антипризмы в 4 измерениях (хотя 16-ячеечную можно рассматривать как правильный аналог двуугольной антипризмы ) . Единственный невыпуклый однородный 4-мерный аналог антипризмы использует пентаграммные скрещенные антипризмы вместо пятиугольных антипризм и называется пентаграммной двойной антипризмой .
Вершинная фигура
[ редактировать ]Вершинная фигура большой антипризмы представляет собой сфенокорону или рассеченный правильный икосаэдр : правильный икосаэдр с удаленными двумя соседними вершинами. Вместо них 8 треугольников заменяются парой трапеций с длиной ребра φ, 1, 1, 1 (где φ — золотое сечение ), соединенных вместе вдоль ребра длиной φ, чтобы получить тетрадекаэдр , грани которого представляют собой две трапеции. и 12 оставшихся равносторонних треугольников .
 12 ( 3.3.3 ) |  2 ( 3.3.3.5 ) |  Рассеченный правильный икосаэдр |
Строительство
[ редактировать ]
Большую антипризму можно построить, уменьшив 600-ячеечную пирамиду : вычитая 20 пирамид, основаниями которых являются трехмерные пятиугольные антипризмы. И наоборот, два кольца пятиугольных антипризм в большой антипризме могут быть триангулированы 10 тетраэдрами, соединенными с треугольными гранями каждой антипризмы, и кругом из 5 тетраэдров между каждой парой антипризм, соединяющим 10 тетраэдров каждой, что дает 150 тетраэдров на каждую. кольцо. В сочетании с 300 тетраэдрами, соединяющими два кольца, получается 600 тетраэдров из 600 ячеек.
Это уменьшение можно реализовать, удалив из 600-ячейки два кольца по 10 вершин, каждое из которых лежит во взаимно ортогональных плоскостях. Каждое кольцо удаленных вершин создает стопку пятиугольных антипризм на выпуклой оболочке . Это соотношение аналогично тому, как пятиугольную антипризму можно построить из икосаэдра , удалив две противоположные вершины, тем самым удалив 5 треугольников с противоположных «полюсов» икосаэдра, оставив 10 экваториальных треугольников и два пятиугольника сверху и снизу.
( Плосконосая 24-ячейка также может быть построена путем еще одного уменьшения 600-ячейки, удаляя 24 икосаэдрических пирамиды. Эквивалентно это можно реализовать, взяв выпуклую оболочку вершин, оставшихся после 24 вершин, соответствующих вершинам вписанной 24-й вершины. -cell удаляются из 600-ячейки.)
Альтернативно, он также может быть построен из декагонального дитетраголтриата (выпуклая оболочка двух перпендикулярных неоднородных дуопризм 10-10 , где соотношение двух декагонов находится в золотом сечении ) посредством процесса чередования . Десятиугольные призмы чередуются с пятиугольными антипризмами , прямоугольные трапезопризмы чередуются с тетраэдрами с двумя новыми правильными тетраэдрами (представляющими некораллическую треугольную бипирамиду ), созданными в удаленных вершинах. Это единственное единое решение для p-угольных двойных антипризмоидов наряду с его сопряженным, пентаграммным двойным антипризмоидом из декаграммного дитетраголтриата.
| 600-ячеечный | Большая антипризма |
|---|---|
| H 4 Самолет Коксетера | |
 | 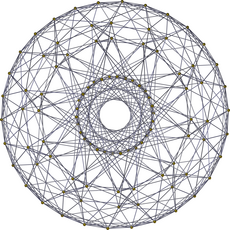 |
| 20-угольный | |
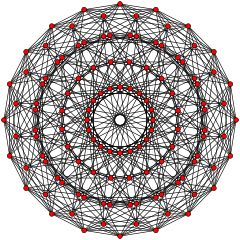 |  |
| H 3 Плоскость Кокстера (небольшое смещение) | |
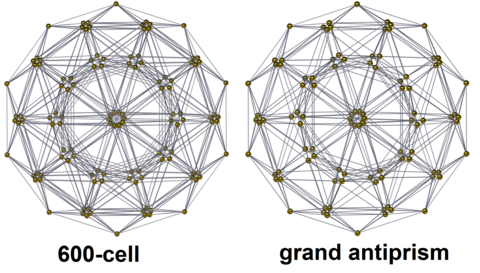 | |
Прогнозы
[ редактировать ]Это две перспективные проекции: проецирование многогранника в гиперсферу и применение стереографической проекции в трехмерное пространство.
 Каркас, вид снизу на одну из пятиугольных колонн-антипризм. |  с прозрачными треугольными гранями |
 Ортографическая проекция Центрировано на гиперплоскости антипризмы в одном из двух колец. | 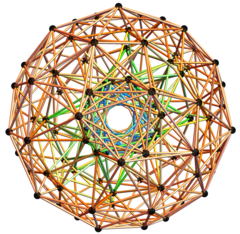 3D ортогональная проекция из 100 из 120 вершин по 600 ячеек и 500 ребер {488 из 1/2 (3-Sqrt[5]) и 12 из 2/(3+Sqrt[5])}. |
См. также
[ редактировать ]Примечания
[ редактировать ]- ^ Дж. Х. Конвей и MJT Гай : Четырехмерные архимедовы многогранники , Материалы коллоквиума по выпуклости в Копенгагене, стр. 38 и 39, 1965. (Майкл Гай - сын Ричарда К. Гая )
- ^ Конвей, 2008, стр.402-403 Великая антипризма.
- ^ Клитцинг, Ричард. «4D выпуклая полихора Большая антипризма» .
Ссылки
[ редактировать ]- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591] 2.8 Великая Антипризма
- Аномальный выпуклый однородный полихорон — Модель 47 , Георгий Ольшевский.
- Клитцинг, Ричард. «Разрыв 4D однородных многогранников (полихоры)» .
- Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (глава 26) Великая антипризма
- Большая антипризма и кватернионы [1] Мехмет Коджа, Мудхахир Аль-Аджми, Назифе Оздес Коджа (2009); Мехмет Коджа и др. 2009 Дж. Физика. А: Математика. теория. 42 495201
Внешние ссылки
[ редактировать ]- В чреве большой антипризмы. Архивировано 7 февраля 2006 г. в Wayback Machine (средняя часть, описывающая аналогию с икосаэдром и пятиугольной антипризмой).