Диаграмма Шлегеля

Примеры раскрашены по количеству сторон на каждой грани. Желтые треугольники , красные квадраты и зеленые пятиугольники .

Тессеракт , спроецированный в трехмерное пространство в виде диаграммы Шлегеля. Видны 8 кубических ячеек : внешняя ячейка, в которую проецируются остальные, по одной под каждой из шести внешних граней и одна в центре.

Различные визуализации икосаэдра

перспектива

Сеть

Ортогональный

Петри

Шлегель

Вершинная фигура

В геометрии диаграмма Шлегеля это проекция многогранника — из ${\textstyle \mathbb {R} ^{d}}$ в ${\textstyle \mathbb {R} ^{d-1}}$ через точку сразу за одной из его граней . Полученная сущность является многогранным подразделением фасета в ${\textstyle \mathbb {R} ^{d-1}}$ который вместе с исходной гранью комбинаторно эквивалентен исходному многограннику. Диаграмма названа в честь Виктора Шлегеля , который в 1886 году представил этот инструмент для изучения комбинаторных и топологических свойств многогранников. В размерности 3 диаграмма Шлегеля представляет собой проекцию многогранника на плоскую фигуру ; в размерности 4 это проекция 4-многогранника в 3-пространство . Таким образом, диаграммы Шлегеля обычно используются как средство визуализации четырехмерных многогранников.

Строительство

Самая элементарная диаграмма Шлегеля, многогранник, была описана Дунканом Соммервилем следующим образом:

Очень полезный метод изображения выпуклого многогранника — проекция на плоскость. Если он проецируется из какой-либо внешней точки, поскольку каждый луч пересекает его дважды, он будет представлен многоугольной областью, разделенной дважды на многоугольники. Всегда можно путем подходящего выбора центра проекции сделать так, чтобы проекция одной грани полностью содержала в себе проекции всех остальных граней. Это называется диаграммой Шлегеля многогранника. Диаграмма Шлегеля полностью отражает морфологию многогранника. Иногда удобно спроецировать многогранник из вершины; эта вершина проецируется на бесконечность и не отображается на диаграмме, ребра, проходящие через нее, представлены линиями, проведенными наружу.

Соммервилль также рассматривает случай симплекса : четырехмерного «Диаграмма Шлегеля симплекса в S ₄ представляет собой тетраэдр, разделенный на четыре тетраэдра». В более общем смысле, многогранник в n-мерных измерениях имеет диаграмму Шлегеля, построенную с помощью перспективной проекции, рассматриваемой из точки вне многогранника, над центром грани. Все вершины и ребра многогранника проецируются на гиперплоскость этой грани. Если многогранник выпуклый, рядом с фасетом будет существовать точка, которая отображает фасет снаружи, а все остальные фасеты внутри, поэтому никакие ребра не должны пересекаться в проекции.

Примеры

Додекаэдр	120-ячеечный
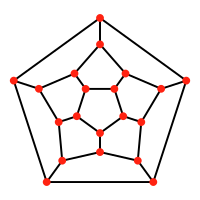12 граней пятиугольника на плоскости	120 додекаэдрических ячеек в 3-мерном пространстве

См. также

• Сеть (многогранник) . Другой подход к визуализации путем уменьшения размерности многогранника заключается в построении сети, отключении граней и развертывании до тех пор, пока грани не смогут существовать в одной гиперплоскости. Это сохраняет геометрический масштаб и форму, но затрудняет видимость топологических связей.

Дальнейшее чтение

• Виктор Шлегель (1883) Теория однородно составленных пространственных структур , Nova Acta, Ksl. Леоп.-Кэрол. Немецкая академия естествоиспытателей, том XLIV, № 4, напечатано E. Blochmann & Sohn в Дрездене. [1]
• Виктор Шлегель (1886) О проекционных моделях правильных четырехмерных тел , Варен.
• Коксетер, HSM ; Правильные многогранники (Methuen and Co., 1948). (стр. 242)
  • Правильные многогранники (3-е издание, 1973 г.), Дуврское издание, ISBN   0-486-61480-8
• Грюнбаум, Бранко (2003), Кайбель, Фолькер; Клее, Виктор ; Циглер, Гюнтер М. (ред.), Выпуклые многогранники (2-е изд.), Нью-Йорк и Лондон: Springer-Verlag , ISBN  0-387-00424-6 .

Внешние ссылки

• Вайсштейн, Эрик В. «График Шлегеля» . Математический мир .
  • Вайсштейн, Эрик В. «Скелет» . Математический мир .
• Джордж Харт: 4D-модели многогранных проекций, созданные с помощью 3D-печати
• Богатая математика – для подростка. Также полезно для учителей.