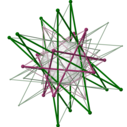
Полигон Петри
В геометрии многоугольник Петри для правильного многогранника измерений n — это косой многоугольник , в котором каждая n –1 последовательная сторона (но не n ) принадлежит одной из граней . Многоугольник Петри правильного многоугольника сам по себе является правильным многоугольником; Правильный многогранник — это косой многоугольник, у которого каждые две последовательные стороны (но не три) принадлежат одной из граней . [1] Многоугольники Петри названы в честь математика Джона Флиндерса Петри .
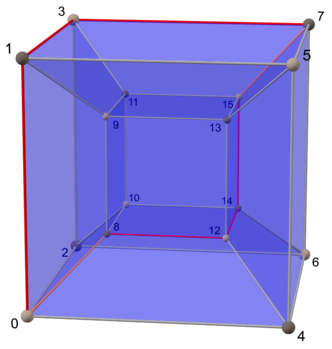
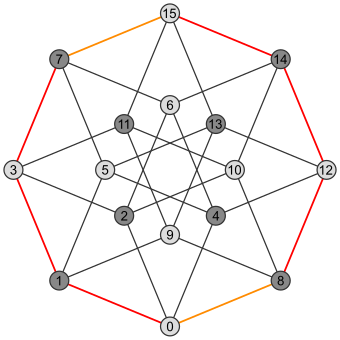
Для каждого правильного многогранника существует ортогональная проекция на плоскость такая, что один многоугольник Петри становится правильным многоугольником, а остальная часть проекции находится внутри него. Рассматриваемая плоскость — это плоскость Кокстера группы симметрии многоугольника, а количество сторон h — это число Кокстера группы Кокстера . Эти многоугольники и проецируемые графы полезны для визуализации симметричной структуры правильных многогранников более высокой размерности.
Полигоны Петри можно определить в более общем смысле для любого встроенного графа . Они образуют грани другого вложения того же графа, обычно на другой поверхности, называемой двойственной Петри . [2]
История [ править ]
Джон Флиндерс Петри (1907–1972) был сыном египтологов Хильды и Флиндерса Петри . Он родился в 1907 году и еще школьником проявил замечательные математические способности. В периоды интенсивной концентрации он мог отвечать на вопросы о сложных четырехмерных объектах, визуализируя их.
Он первым отметил важность правильных косых многоугольников, которые появляются на поверхности правильных многогранников и высших многогранников. В 1937 году Коксетер объяснил, как он и Петри начали расширять классическую тему правильных многогранников:
- Однажды в 1926 году Дж. Ф. Петри с большим волнением рассказал мне, что он открыл два новых правильных многогранника; бесконечно, но без ложных вершин. Когда мое недоверие начало утихать, он описал их мне: один, состоящий из квадратов, по шесть в каждой вершине, и один, состоящий из шестиугольников, по четыре в каждой вершине. [3]
В 1938 году Петри сотрудничал с Кокстером, Патриком дю Валем и Х. Т. Флатером для подготовки к публикации книги «Пятьдесят девять икосаэдров» . [4] Понимая геометрическую легкость косых многоугольников, использованных Петри, Коксетер назвал их в честь своего друга, когда он написал « Правильные многогранники» .
Позднее идея многоугольников Петри была распространена на полуправильные многогранники .
Многоугольники Петри правильных многогранников [ править ]
Правильные двойственные числа { p , q } и { q , p } содержатся в одном и том же спроецированном многоугольнике Петри.На изображениях дуальных соединений справа видно, что их многоугольники Петри имеют прямоугольные пересечения в точках соприкосновения ребер с общей срединной сферой .
| Квадрат | Шестиугольник | Декагон | ||
|---|---|---|---|---|
 |  |  | 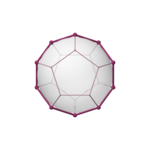 |  |
| тетраэдр {3,3} | куб {4,3} | октаэдр {3,4} | додекаэдр {5,3} | икосаэдр {3,5} |
| по краю | вершинно-центрированный | сосредоточенный на лице | сосредоточенный на лице | вершинно-центрированный |
| V :(4,0) | V :(6,2) | V :(6,0) | V :(10,10,0) | V :(10,2) |
Многоугольники Петри представляют собой внешнюю сторону этих ортогональных проекций. | ||||
Многоугольники Петри многогранников Кеплера–Пуансо представляют собой шестиугольники {6} и декаграммы {10/3}.
| Шестиугольник | Декаграмма | ||
|---|---|---|---|
 |  |  |  |
| гД {5,5/2} | СД {5,5/2} | гI {3,5/2} | гсД {5/2,3} |
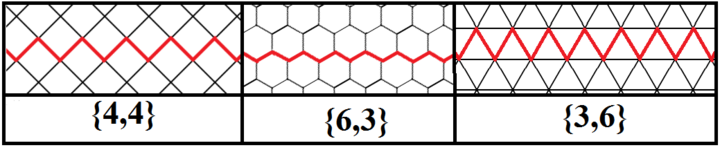
Бесконечные правильные косые многоугольники ( апейрогоны ) также можно определить как многоугольники Петри правильных мозаик с углами 90, 120 и 60 градусов на их квадратных, шестиугольных и треугольных гранях соответственно.
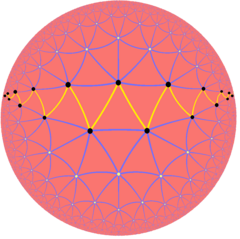
Бесконечные правильные косые многоугольники также существуют как многоугольники Петри правильных гиперболических мозаик, таких как треугольная мозаика 7-го порядка , {3,7}:
Многоугольник Петри правильной полихоры (4 многогранника - )
Многоугольник Петри для правильной полихоры { p , q , r } также может быть определен так, что каждые три последовательные стороны (но не четыре) принадлежат одной из ячеек полихоры. Поскольку поверхность 4-многогранника представляет собой 3-мерное пространство ( 3-сфера ), многоугольник Петри правильного 4-многогранника представляет собой 3-мерную спираль на этой поверхности.
 {3,3,3} 5-клеточный 5 сторон V :(5,0) | 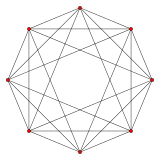 {3,3,4} 16-ячеечный 8 сторон V :(8,0) |  {4,3,3} тессеракт 8 сторон V :(8,8,0) |
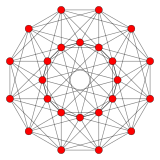 {3,4,3} 24-ячеечный 12 сторон V :(12,6,6,0) | 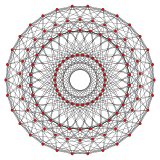 {3,3,5} 600-ячеечный 30 сторон V:(30,30,30,30,0) |  {5,3,3} 120-ячеечный 30 сторон V :((30,60) 3 ,60 3 ,30,60,0) |
Многоугольные проекции Петри правильных и однородных многогранников
Проекции многоугольников Петри полезны для визуализации многогранников размерности четыре и выше.
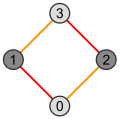
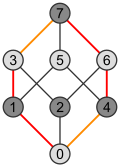
Гиперкубы [ править ]
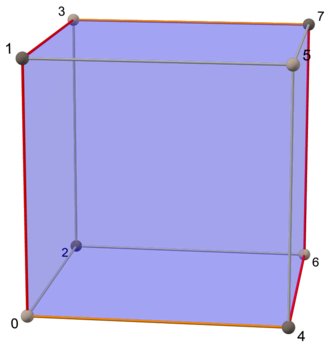
Гиперкуб граней размерности n имеет многоугольник Петри размера 2 n что также соответствует числу его . ,
Таким образом, каждый из ( n − 1)-кубов, образующих его поверхность, имеет среди своих ребер n − 1 сторону многоугольника Петри.
| Гиперкубы |
|---|
Семейства неприводимых многогранников [ править ]
В этой таблице представлены проекции многоугольников Петри трех правильных семейств ( симплекс , гиперкуб , ортоплекс ) и исключительной группы Ли En , которые порождают полуправильные и однородные многогранники для размерностей от 4 до 8.
| Таблица семейств неприводимых многогранников | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Семья н | n - симплекс | n - гиперкуб | n - ортоплекс | n - демикуб | 1 к2 | 2 к1 | до 21 числа | пятиугольный многогранник | ||||||||
| Группа | н | Б н |
|
| Ч н | |||||||||||
| 2 |  |  |  п-гон (пример: p=7 ) |  Шестиугольник |  Пентагон | |||||||||||
| 3 |  Тетраэдр |  Куб |  Октаэдр |  Тетраэдр |  Додекаэдр |  Икосаэдр | ||||||||||
| 4 |  5-клеточный |  |  16-ячеечный |  |  24-ячеечный |  120-ячеечный |  600-ячеечный | |||||||||
| 5 |  5-симплекс |  5-куб |  5-ортоплекс |  5-демикуб | ||||||||||||
| 6 |  6-симплекс |  6-куб. |  6-ортоплекс |  6-демикуб |  1 22 |  2 21 | ||||||||||
| 7 |  7-симплекс |  7-куб |  7-ортоплекс |  7-демикуб |  1 32 |  2 31 |  3 21 | |||||||||
| 8 |  8-симплекс |  8-кубовый |  8-ортоплекс |  8-демикуб |  1 42 |  2 41 |  4 21 | |||||||||
| 9 |  9-симплекс |  9-куб |  9-ортоплекс |  9-демикуб | ||||||||||||
| 10 |  10-симплекс |  10-кубовый |  10-ортоплекс |  10-демикуб | ||||||||||||
См. также [ править ]
Примечания [ править ]
- ^ Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена , Энтони К. Томпсона, Асии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] (Определение: статья 13, Дискретные группы, порожденные отражениями, 1933, стр. 161)
- ^ Горини, Кэтрин А. (2000), Геометрия в работе , Примечания MAA, том. 53, Издательство Кембриджского университета, стр. 53. 181, ISBN 9780883851647
- ^ HSM Coxeter (1937) «Правильные косые многогранники в трех и четырех измерениях и их топологические аналоги», Труды Лондонского математического общества (2) 43: 33–62
- ^ HSM Коксетер, Патрик дю Валь , HT Flather, JF Petrie (1938) Пятьдесят девять икосаэдров , исследования Университета Торонто , математические серии 6: 1–26
- ^ http://cms.math.ca/openaccess/cjm/v10/cjm1958v10.0220-0221.pdf [ мертвая ссылка ]
Ссылки [ править ]
- Коксетер , HSM (1947, 63, 73) Правильные многогранники , 3-е изд. Нью-Йорк: Дувр, 1973. (раздел 2.6 «Многоугольники Петри» , стр. 24–25, и глава 12, стр. 213–235, «Обобщенный многоугольник Петри» )
- Коксетер, HSM (1974) Правильные комплексные многогранники . Раздел 4.3 Флаги и ортосхемы, Раздел 11.3 Многоугольники Петри
- Болл, WWR и HSM Coxeter (1987) Математические развлечения и очерки , 13-е изд. Нью-Йорк: Дувр. (стр. 135)
- Коксетер, HSM (1999) Красота геометрии: двенадцать эссе , Dover Publications LCCN 99-35678
- Питер МакМаллен , Эгон Шульте (2002) Абстрактные правильные многогранники , издательство Кембриджского университета . ISBN 0-521-81496-0
- Стейнберг, Роберт, О ЧИСЛЕ СТОРОН МНОГОУГОЛЬНИКА ПЕТРИ , 2018 г. [2]
Внешние ссылки [ править ]
- Вайсштейн, Эрик В. «Многоугольник Петри» . Математический мир .
- Вайсштейн, Эрик В. «Графы гиперкуба» . Математический мир .
- Вайсштейн, Эрик В. «Перекрестные многогранные графы» . Математический мир .
- Вайсштейн, Эрик В. «24-клеточный граф» . Математический мир .
- Вайсштейн, Эрик В. «Граф из 120 ячеек» . Математический мир .
- Вайсштейн, Эрик В. «Граф с 600 ячейками» . Математический мир .
- Вайсштейн, Эрик В. «График Госсета 3_21» . Математический мир .