2 41 многогранник

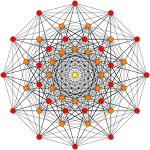4 21	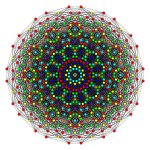1 42	2 41
Исправлено 4 21	Исправлено 1 42	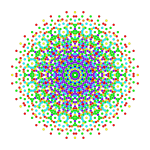Исправлено 2 41
Биректифицированный 4 21	Триректифицированный 4 21
Ортогональные проекции в E 6 плоскости Кокстера

В 8-мерной 41 — геометрии 2 _это однородный 8-многогранник , построенный в рамках симметрии группы E ₈ .

Его символ Кокстера — 2 ₄₁ , описывающий его разветвляющуюся диаграмму Кокстера-Дынкина с одним кольцом на конце двухузловой последовательности.

Выпрямленный 2 ₄₁ строится по точкам на средних краях 2 ₄₁ . Биректифицированное 2 ₄₁ построено точками в центрах треугольных граней 2 ₄₁ и совпадает с выпрямленным 1 ₄₂ .

Эти многогранники являются частью семейства из 255 (2 ⁸ − 1) выпуклые однородные многогранники в 8-мерном измерении, состоящие из однородных граней многогранника , определяемые всеми перестановками колец в этой диаграмме Кокстера-Дынкина : .

2 ₄₁ многогранник

2 41 многогранник
Тип	Равномерный 8-многогранник
Семья	2 k1 Многогранник
Символ Шлефли	{3,3,3 4,1 }
Символ Коксетера	2 41
Диаграмма Кокстера
7-гранный	17520: 240 2 31 17280 {3 6 }
6-гранный	144960: 6720 2 21 138240 {3 5 }
5-гранный	544320: 60480 2 11 483840 {3 4 }
4-ликий	1209600: 241920 {2 01 967680 {3 3 }
Клетки	1209600 {3 2 }
Лица	483840 {3}
Края	69120
Вершины	2160
Вершинная фигура	1 41
Полигон Петри	30-угольник
Группа Коксетера	Е 8 , [3 4,2,1 ]
Характеристики	выпуклый

2 6 ₄₁ состоит из 17 520 граней (240 2 ₃₁ многогранников и 17 280 7-симплексов ), 144 960 6-граней (6 720 2 ₂₁ многогранников и 138 240 -симплексов ), 544 320 5-граней (60 480 2 ₁₁ и 483, 840 5-симплексов ) , 1 209 600 4-граней ( 4-симплекса ), 1 209 600 ячеек ( тетраэдров ), 483 840 граней ( треугольников ), 69 120 ребер и 2160 вершин . Его вершинная фигура — семикуб .

Этот многогранник является гранью однородной мозаики 2 ₅₁ с диаграммой Кокстера-Динкина :

Альтернативные названия

• Э. Л. Эльте назвал его V ₂₁₆₀ (за 2160 вершин) в своем списке полуправильных многогранников 1912 года.
• назвал его 41 _в Коксетер 2 честь разветвляющейся диаграммы Кокстера-Динкина с одним кольцом на конце последовательности из двух узлов.
• Diacositetracont-myriaheptachiliadiacosioctaconta-zetton (Acronym Bay) - 240-17280 граненый полизеттон (Jonathan Bowers)

2160 вершин можно определить следующим образом:

16 перестановок (±4,0,0,0,0,0,0,0) из ( 8-ортоплекса )

1120 перестановок (±2,±2,±2,±2,0,0,0,0) из ( триректифицированного 8-ортоплекса )

1024 перестановки (±3,±1,±1,±1,±1,±1,±1,±1) с нечетным количеством знаков минус

Строительство

Он создан с помощью конструкции Витхоффа на основе набора из 8 гиперплоских зеркал в 8-мерном пространстве.

Информацию о фасетах можно извлечь из диаграммы Кокстера-Динкина : .

Удаление узла на короткой ветви оставляет 7-симплекс : . Всего таких граней 17280.

Удаление узла на конце ветки длиной 4 оставляет 2 ₃₁ , . Таких граней 240. Они центрированы в позициях 240 вершин многогранника 4 ₂₁ .

Фигура вершины определяется путем удаления окольцованного узла и окольцовывания соседнего узла. Получается 7-демикуб , 1 ₄₁ , .

В матрице конфигурации количество элементов может быть получено путем удаления зеркал и соотношений групповых порядков Кокстера .

show		Матрица конфигурации
E8		k-face	fk	f0	f1	f2	f3	f4		f5		f6		f7		k-figure	notes
D7		( )	f0	2160	64	672	2240	560	2240	280	1344	84	448	14	64	h{4,3,3,3,3,3}	E8/D7 = 192*10!/64/7! = 2160
A6A1		{ }	f1	2	69120	21	105	35	140	35	105	21	42	7	7	r{3,3,3,3,3}	E8/A6A1 = 192*10!/7!/2 = 69120
A4A2A1		{3}	f2	3	3	483840	10	5	20	10	20	10	10	5	2	{}x{3,3,3}	E8/A4A2A1 = 192*10!/5!/3!/2 = 483840
A3A3		{3,3}	f3	4	6	4	1209600	1	4	4	6	6	4	4	1	{3,3}V( )	E8/A3A3 = 192*10!/4!/4! = 1209600
A4A3		{3,3,3}	f4	5	10	10	5	241920	*	4	0	6	0	4	0	{3,3}	E8/A4A3 = 192*10!/5!/4! = 241920
A4A2				5	10	10	5	*	967680	1	3	3	3	3	1	{3}V( )	E8/A4A2 = 192*10!/5!/3! = 967680
D5A2		{3,3,31,1}	f5	10	40	80	80	16	16	60480	*	3	0	3	0	{3}	E8/D5A2 = 192*10!/16/5!/2 = 40480
A5A1		{3,3,3,3}		6	15	20	15	0	6	*	483840	1	2	2	1	{ }V( )	E8/A5A1 = 192*10!/6!/2 = 483840
E6A1		{3,3,32,1}	f6	27	216	720	1080	216	432	27	72	6720	*	2	0	{ }	E8/E6A1 = 192*10!/72/6! = 6720
A6		{3,3,3,3,3}		7	21	35	35	0	21	0	7	*	138240	1	1		E8/A6 = 192*10!/7! = 138240
E7		{3,3,33,1}	f7	126	2016	10080	20160	4032	12096	756	4032	56	576	240	*	( )	E8/E7 = 192*10!/72!/8! = 240
A7		{3,3,3,3,3,3}		8	28	56	70	0	56	0	28	0	8	*	17280		E8/A7 = 192*10!/8! = 17280

Визуализации

Проекция числа 2 ₄₁ на плоскость Кокстера E ₈ (она же проекция Петри) с радиусом многогранника. $2{\sqrt {2}}$ и 69120 ребер длины $2{\sqrt {2}}$

Показано в 3D-проекции с использованием базисных векторов [u,v,w], обеспечивающих симметрию H3:

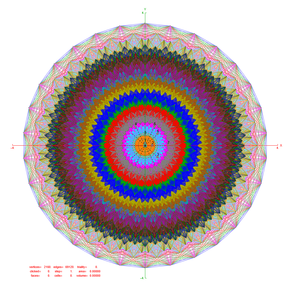
• ты = (1, φ , 0, −1, φ , 0,0,0)
• v = ( φ , 0, 1, φ , 0, −1,0,0)
• ш = (0, 1, φ , 0, −1, φ ,0,0)

2160 спроецированных 2 ₄₁ вершин многогранников сортируются и подсчитываются по их трехмерным нормам, создавая все более прозрачные оболочки для каждого набора подсчитанных норм. Перекрывающиеся вершины имеют цветовую маркировку в зависимости от количества перекрытий. Также показан список каждой группы оболочек, нормированное расстояние от начала координат и количество вершин в группе.

Спроецированный многогранник 2160 2 ₄₁ спроецирован в 3D (как указано выше), при этом каждая нормированная группа оболочек указана индивидуально с количеством вершин. Обратите внимание, что последние две внешние оболочки представляют собой комбинацию двух перекрывающихся икосаэдров (24) и икосододекаэдра (30).

Е8 [30]	[20]	[24]
(1)
E7 [18]	Е6 [12]	[6]
	(1,8,24,32)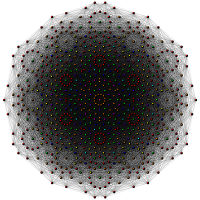

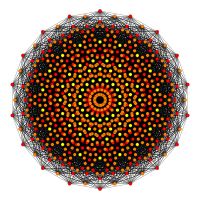
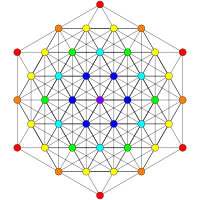
Проекции многоугольников Петри имеют 12, 18 или 30 сторон на основе симметрии E6, E7 и E8 (соответственно). Все 2160 вершин отображаются, но формы с более низкой симметрией имеют перекрывающиеся проекции, показанные вершинами разного цвета. Для сравнения также показана группа Кокстера B6.

Д3/Б2/А3 [4]	Д4/Б3/А2 [6]	Д5/В4 [8]
Д6/В5/А4 [10]	D7 / B6 [12]	Д8/В7/А6 [14]
	(1,3,9,12,18,21,36)
Б8 [16/2]	А5 [6]	A7 [8]

Связанные многогранники и соты

показывать 2 k 1 фигур в n измерениях
Space	Finite						Euclidean	Hyperbolic
n	3	4	5	6	7	8	9	10
Coxeter group	E3=A2A1	E4=A4	E5=D5	E6	E7	E8	E9 = ${\tilde {E}}_{8}$ = E8+	E10 = ${\bar {T}}_{8}$ = E8++
Coxeter diagram
Symmetry	[3−1,2,1]	[30,2,1]	[[31,2,1]]	[32,2,1]	[33,2,1]	[34,2,1]	[35,2,1]	[36,2,1]
Order	12	120	384	51,840	2,903,040	696,729,600	∞
Graph							-	-
Name	2−1,1	201	211	221	231	241	251	261

Выпрямленный многогранник 2_41

2 41 Выпрямленный многогранник
Тип	Равномерный 8-многогранник
Символ Шлефли	т 1 {3,3,3 4,1 }
Символ Коксетера	т 1 (2 41 )
Диаграмма Кокстера
7-гранный	19680 всего: 240 т 1 (2 21 ) 17280 т 1 {3 6 } 2160 1 41
6-гранный	313440
5-гранный	1693440
4-ликий	4717440
Клетки	7257600
Лица	5322240
Края	19680
Вершины	69120
Вершинная фигура	выпрямленная 6-симплексная призма
Полигон Петри	30-угольник
Группа Коксетера	Е 8 , [3 4,2,1 ]
Характеристики	выпуклый

Выпрямленный многогранник 2 ₄₁ представляет собой выпрямление многогранника 2 ₄₁ с вершинами, расположенными на средних краях 2 ₄₁ .

Альтернативные названия

• Ректифицированный диакозитетраконт-мириагептахилиадиакозиоктаконта-зеттон для ректифицированного граненого полизеттона 240-17280 (сокращенно известного как робей)

Строительство

Он создается с помощью конструкции Витхоффа на наборе из 8 гиперплоских зеркал в 8-мерном пространстве, заданном корневыми векторами E ₈ группы Коксетера .

Информацию о фасетах можно извлечь из диаграммы Кокстера-Динкина : .

Удаление узла на короткой ветви оставляет исправленный 7-симплекс : .

Удаление узла на конце ветви длиной 4 оставляет выпрямленный 2 ₃₁ , .

При удалении узла на конце ветви длиной 2 остается полукуб длиной 7 , 1 ₄₁ .

Фигура вершины определяется путем удаления окольцованного узла и окольцовывания соседнего узла. Это делает выпрямленную 6-симплексную призму .

Визуализации

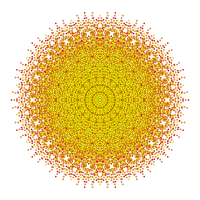
Проекции многоугольников Петри имеют 12, 18 или 30 сторон на основе симметрии E6, E7 и E8 (соответственно). Все 2160 вершин отображаются, но формы с более низкой симметрией имеют перекрывающиеся проекции, показанные вершинами разного цвета. Для сравнения также показана группа Кокстера B6.

Е8 [30]	[20]	[24]
(1)
E7 [18]	Е6 [12]	[6]
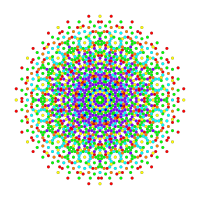	(1,8,24,32)

Д3/Б2/А3 [4]	Д4/Б3/А2 [6]	Д5/В4 [8]
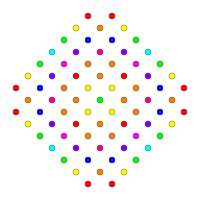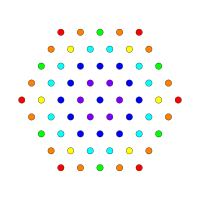Д6/В5/А4 [10]	D7 / B6 [12]	Д8/В7/А6 [14]
	(1,3,9,12,18,21,36)
Б8 [16/2]	А5 [6]	A7 [8]

См. также

• Список многогранников E8

Ссылки

• Эльте, EL (1912), Полуправильные многогранники гиперпространств , Гронинген: Гронингенский университет.
• HSM Coxeter , Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
• Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6 [1]
  • (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
• Клитцинг, Ричард. «8D Униформа Полизетта» . x3o3o3o *c3o3o3o3o - залив, o3x3o3o *c3o3o3o3o - робей