Символ Шлефли

Додекаэдр пятиугольника — правильный многогранник с символом Шлефли {5,3}, имеющий по три вокруг каждой вершины .

В геометрии символ Шлефли — обозначение вида $\{p,q,r,...\}$ который определяет правильные многогранники и мозаики .

Символ Шлефли назван в честь швейцарского математика XIX века Людвига Шлефли . который обобщил евклидову геометрию на более чем три измерения и открыл все ее выпуклые правильные многогранники, включая шесть, встречающиеся в четырех измерениях.

Определение

Символ Шлефли представляет собой рекурсивное описание, начиная с { p } для p -стороннего правильного многоугольника , который является выпуклым . Например, {3} — равносторонний треугольник , {4} — квадрат , {5} — выпуклый правильный пятиугольник и т. д.

Правильные звездчатые многоугольники не являются выпуклыми, и их символы Шлефли { ^п / _q } содержат несократимые дроби ^п / _q , где p — количество вершин, а q — число их поворотов . Эквивалентно, { ^п / _q } создается из вершин { p }, связанных с каждым q . Например, { 5 ⁄ 2 } — пентаграмма ; { 5/1 ​ пятиугольник } — .

Правильный многогранник , у которого есть q граней правильного p -стороннего многоугольника вокруг каждой вершины , обозначается { p , q }. Например, куб имеет три квадрата вокруг каждой вершины и обозначается {4,3}.

Правильный 4-мерный многогранник с r { p , q } правильными многогранными ячейками вокруг каждого ребра обозначается { p , q , r }. Например, тессеракт {4,3,3} имеет 3 куба {4,3} по краю.

В общем, правильный многогранник { p , q , r ,..., y , z } имеет z { p , q , r ,..., y } граней вокруг каждой вершины , где вершина — это вершина многогранника. , ребро в 4-многограннике, грань в 5-многограннике и ( n -3)-грань в n -многограннике.

Характеристики

Правильный многогранник имеет правильную вершинную фигуру . Вершинная фигура правильного многогранника { p , q , r ,..., y , z } равна { q , r ,..., y , z }.

Правильные многогранники могут иметь звездчатого многоугольника элементы , такие как пентаграмма , с символом { 5 ⁄ 2 }, представленный вершинами пятиугольника , но соединенными попеременно.

Символ Шлефли может представлять собой конечный выпуклый многогранник , бесконечную мозаику евклидова пространства или бесконечную мозаику гиперболического пространства , в зависимости от углового дефекта конструкции. Дефект положительного угла позволяет вершинной фигуре сворачиваться в более высокое измерение и возвращаться в себя как многогранник. Дефект с нулевым углом замощает пространство того же размера, что и грани. Дефект отрицательного угла не может существовать в обычном пространстве, но может быть построен в гиперболическом пространстве.

Обычно фасет или вершинная фигура считается конечным многогранником, но иногда сама по себе может считаться мозаикой.

Правильный многогранник также имеет двойственный многогранник , представленный элементами символа Шлефли в обратном порядке. Самодуальный правильный многогранник будет иметь симметричный символ Шлефли.

Помимо описания евклидовых многогранников, символы Шлефли можно использовать для описания сферических многогранников или сферических сот.

История и вариации

Работа Шлефли была почти неизвестна при его жизни, а его обозначения для описания многогранников были независимо заново открыты несколькими другими. В частности, Торольд Госсет заново открыл символ Шлефли, который он написал как |   р   |   д   |   р   |   ...   |   г   | а не скобками и запятыми, как это сделал Шлефли.

Форма Госсета имеет большую симметрию, поэтому количество измерений равно количеству вертикальных полос, а символ точно включает в себя подсимволы для фасетной и вершинной фигуры. Госсет считает |   p как оператор, который можно применить к |   д   |   ...   |   г   | создать многогранник с p -угольными гранями, фигура вершины которого равна |   д   |   ...   |   г   |.

Случаи

Группы симметрии

Символы Шлефли тесно связаны с (конечными) отражения группами симметрии , которые точно соответствуют конечным группам Кокстера и задаются теми же индексами, но вместо них используются квадратные скобки [ p , q , r ,...]. Такие группы часто называют по образу правильных многогранников, которые они порождают. Например, [3,3] — это группа Коксетера для отражающей тетраэдрической симметрии , [3,4] — для отражающей октаэдрической симметрии , а [3,5] — для отражающей икосаэдрической симметрии .

Правильные многоугольники (плоскость)

Правильные выпуклые и звездчатые многоугольники с от 3 до 12 вершин, помеченные символами Шлефли.

Символ Шлефли выпуклого правильного многоугольника с p ребрами — { p }. Например, правильный пятиугольник обозначается {5}.

Для невыпуклых звездчатых многоугольников конструктивное обозначение { p ⁄ q }, где p — количество вершин, а q −1 — количество вершин, пропущенных при рисовании каждого края звезды. Например, { 5 ⁄ 2 } представляет пентаграмму .

Правильные многогранники (3 измерения)

Символом Шлефли правильного многогранника является { p , q }, если его грани являются p -угольниками, а каждая вершина окружена q гранями ( фигура вершины - q -угольник).

Например, {5,3} — правильный додекаэдр . Он имеет пятиугольные (5 ребер) грани и по 3 пятиугольника вокруг каждой вершины.

См. 5 выпуклых Платоновых тел , 4 невыпуклых многогранника Кеплера-Пуансо .

Топологически правильную двумерную мозаику можно рассматривать как подобную (3-мерному) многограннику, но такую, что угловой дефект равен нулю. Таким образом, символы Шлефли также могут быть определены для правильных мозаик евклидова . или гиперболического пространства аналогично тому, как это делается для многогранников Аналогия справедлива и для более высоких измерений.

Например, шестиугольная мозаика представлена ​​{6,3}.

Правильные 4-многогранники (4 измерения)

Символ Шлефли правильного 4-многогранника имеет вид { p , q , r }. Его (двумерные) грани представляют собой правильные p -угольники ({ p }), ячейки — правильные многогранники типа { p , q }, фигуры вершин — правильные многогранники типа { q , r }, а реберные фигуры — правильные r -угольники (типа { r }).

См. шесть выпуклых правильных и 10 правильных звездчатых 4-многогранников .

Например, 120-ячейка представлена ​​{5,3,3}. Он состоит из ячеек додекаэдра {5,3} и имеет по 3 ячейки вокруг каждого края.

Существует одна правильная мозаика евклидова трехмерного пространства: кубические соты с символом Шлефли {4,3,4}, состоящие из кубических ячеек и четырех кубов по каждому краю.

Есть также 4 регулярных компактных гиперболических мозаики, включая {5,3,4}, небольшие гиперболические соты додекаэдра , которые заполняют пространство ячейками додекаэдра .

Если символ 4-многогранника является палиндромным (например, {3,3,3} или {3,4,3}), его битовое усечение будет иметь только усеченные формы вершинной фигуры в виде ячеек.

Правильные n -многогранники (более высокие размерности)

более высокой размерности Для правильных многогранников символ Шлефли определяется рекурсивно как { p ₁ , p ₂ , ..., p _{n - 1} }, если грани имеют символ Шлефли { p ₁ , p ₂ , ..., p _{n - 2} } и вершинные фигуры имеют символ Шлефли { p ₂ , p ₃ , ..., p _{n − 1} } .

Фигура вершины грани многогранника и грань вершины фигуры того же многогранника одинаковы: { p ₂ , p ₃ , ..., p _{n − 2} } .

Есть только 3 правильных многогранника в 5 измерениях и выше: симплекс , {3, 3, 3, ..., 3}; перекрестный многогранник , {3, 3, ..., 3, 4}; и гиперкуб , {4, 3, 3, ..., 3}. Невыпуклых правильных многогранников выше 4 измерений не существует.

Двойные многогранники

Если многогранник размерности n   ≥   2 имеет символ Шлефли {   p ₁ , p ₂ , ..., p _{n   −   1}   }, то его двойственный многогранник имеет символ Шлефли {   p _{n   −   1} , ..., p ₂ , p ₁   }.

Если последовательность палиндромна , то есть одинакова вперед и назад, многогранник самодвойственный . Каждый правильный двумерный многогранник (многоугольник) самодуален.

Призматические многогранники

Однородные призматические многогранники можно определить и назвать как декартово произведение (с оператором «×») правильных многогранников меньшей размерности.

• В 0D точка обозначается ( ). Его диаграмма Кокстера пуста. Его симметрия в обозначениях Кокстера равна ][.
• В 1D сегмент линии представлен {}. Его диаграмма Кокстера : . Его симметрия [ ].
• В 2D прямоугольник представлен как { } × { }. Его диаграмма Кокстера : . Его симметрия [2].
• В 3D p -угольная призма представлена ​​как { } × { p }. Его диаграмма Кокстера: . Его симметрия равна [2, p ].
• В 4D однородная { p , q }-эдральная призма представлена ​​как { } × { p , q }. Его диаграмма Кокстера: . Его симметрия равна [2, p , q ].
• В 4D однородная p - q дуопризма представлена ​​как { p } × { q }. Его диаграмма Кокстера: . Его симметрия — [ p ,2, q ].

Призматические двойники или бипирамиды могут быть представлены в виде составных символов, но с оператором сложения «+».

• В 2D ромб представлен как { } + { }. Его диаграмма Кокстера: . Его симметрия [2].
• В 3D p -угольная бипирамида представлена ​​как { } + { p }. Его диаграмма Кокстера: . Его симметрия равна [2, p ].
• В 4D { p , q }-эдральная бипирамида представлена ​​как { } + { p , q }. Его диаграмма Кокстера: . Его симметрия — [ p , q ].
• В 4D p - q дуопирамида представлена ​​как { p } + { q }. Его диаграмма Кокстера: . Его симметрия — [ p ,2, q ].

Пирамидальные многогранники, содержащие ортогонально смещенные вершины, можно представить с помощью оператора соединения «∨». Каждая пара вершин между соединенными фигурами соединена ребрами.

В 2D равнобедренный треугольник можно представить как ( ) ∨ { } = ( ) ∨ [( ) ∨ ( )].

В 3D:

• можно Двуугольный дисфеноид представить в виде { } ∨ { } = [( ) ∨ ( )] ∨ [( ) ∨ ( )].
• представляется p-угольная пирамида как ( ) ∨ { p }.

И 4D:

• Pq -эдральная пирамида изображается как ( ) ∨ { p , q }.
• представляется 5-ячейка как ( ) ∨ [( ) ∨ {3}] или [( ) ∨ ( )] ∨ {3} = { } ∨ {3}.
• Квадратная пирамидальная пирамида представляется как ( ) ∨ [( ) ∨ {4}] или [( ) ∨ ( )] ∨ {4} = { } ∨ {4}.

При смешивании операторов порядок операций от высшего к низшему равен ×, +, ∨.

Осевые многогранники, содержащие вершины на параллельных гиперплоскостях смещения, могут быть представлены оператором ‖. Однородная призма — это { n }‖{ n } и антипризма { n }‖ r { n }.

Расширение символов Шлефли

Многоугольники и круговые мозаики

Усеченный правильный многоугольник сдвоился по сторонам. Правильный многоугольник с четными сторонами можно разделить пополам. Измененный четносторонний правильный 2n-угольник образует соединение звездной фигуры 2{n}.

Форма	Символ Шлефли	Симметрия	Диаграмма Кокстера		Пример, {6}
Обычный	{р}	[п]				Шестиугольник
Усечено	т{р} = {2р}	[[п]] = [2п]	=			Усеченный шестиугольник (Додекагон)	=
Измененный и Голосорванный	а{2р} = β{р}	[2р]	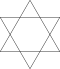=			Измененный шестиугольник (Гексаграмма)	=
Половина и пренебрежительно	h{2p} = s{p} = {p}	[1 + ,2p] = [p]	= =			Половина шестиугольника (Треугольник)	= =

Многогранники и мозаики

Коксетер расширил использование символа Шлефли до квазиправильных многогранников , добавив к символу вертикальное измерение. Это была отправная точка на пути к более общей диаграмме Кокстера . Норман Джонсон упростил обозначение вертикальных символов с помощью префикса r . Т-обозначение является наиболее общим и напрямую соответствует кольцам диаграммы Кокстера. Символы имеют соответствующее чередование заменяются : кольца отверстиями . Конструкция ограничена требованием , на диаграмме Коксетера, а префикс h обозначает половину чтобы соседние ветви были четными, и сокращает порядок симметрии вдвое. Связанный оператор a для altered показан с двумя вложенными отверстиями и представляет собой составные многогранники с обеими чередующимися половинами, сохраняя исходную полную симметрию. Курносый — это половинная форма усечения, а голоснос — обе половины попеременного усечения.

Форма	Символы Шлефли			Симметрия	Диаграмма Кокстера		Пример, {4,3}
Обычный	${\begin{Bmatrix}p,q\end{Bmatrix}}$	{п, д}	т 0 {p,q}	[п, д] или [(p,q,2)]				Куб
Усечено	$t{\begin{Bmatrix}p,q\end{Bmatrix}}$	t{p,q}	т 0,1 {p,q}					Усеченный куб
Биусечение (усеченный двойной)	$t{\begin{Bmatrix}q,p\end{Bmatrix}}$	2t{p,q}	т 1,2 {p,q}					Усеченный октаэдр
Исправленный ( Квазирегулярный )	${\begin{Bmatrix}p\\q\end{Bmatrix}}$	г {р, q}	т 1 {p,q}					Кубооктаэдр
Биректификация (Обычный двойной)	${\begin{Bmatrix}q,p\end{Bmatrix}}$	2r{p,q}	т 2 {p,q}					Октаэдр
Отмененный ( Исправлено исправлено )	$r{\begin{Bmatrix}p\\q\end{Bmatrix}}$	rr{p,q}	т 0,2 {p,q}					Ромбокубооктаэдр
Количество сокращено (Усечено исправлено)	$t{\begin{Bmatrix}p\\q\end{Bmatrix}}$	tr{p,q}	т 0,1,2 {p,q}					Усеченный кубооктаэдр

Чередования, четверти и пренебрежения

Чередования имеют половину симметрии групп Кокстера и представлены незаполненными кольцами. Возможны два варианта, при которых будет взята половина вершин, но символ не указывает, какой из них. Четвертные формы показаны здесь со знаком + внутри полого кольца, что означает, что это два независимых чередования.

Чередования

Форма	Символы Шлефли			Симметрия	Диаграмма Кокстера		Пример, {4,3}
Альтернативный (полу) обычный	$h{\begin{Bmatrix}2p,q\end{Bmatrix}}$	ч{2p,q}	ht 0 {2p,q}	[1 + ,2p,q]	=			Демикуб ( Тетраэдр )
Курносый обычный	$s{\begin{Bmatrix}p,2q\end{Bmatrix}}$	с{п,2q}	ht 0.1 {p,2q}	[п + ,2q]
Курносый двойной обычный	$s{\begin{Bmatrix}q,2p\end{Bmatrix}}$	с {q, 2p}	чт 1,2 {2p,q}	[2p,q + ]				Курносый октаэдр ( Икосаэдр )
Попеременный выпрямленный (p и q четные)	$h{\begin{Bmatrix}p\\q\end{Bmatrix}}$	час {p, q}	ht 1 {p,q}	[п,1 + ,q]
Попеременный выпрямленный выпрямленный (p и q четные)	$hr{\begin{Bmatrix}p\\q\end{Bmatrix}}$	чрр{p,q}	ht 0,2 {p,q}	[(p,q,2 + )]
четвертован (p и q четные)	$q{\begin{Bmatrix}p\\q\end{Bmatrix}}$	q{p,q}	ht 0 ht 2 {p,q}	[1 + ,п,д,1 + ]
Курносый исправлен Курносый квазирегулярный	$s{\begin{Bmatrix}p\\q\end{Bmatrix}}$	ср{п,q}	ht 0,1,2 {p,q}	[п, д] +				Курносый кубооктаэдр (Курносый куб)

Переделанный и голоснубированный

Измененные и голосубые формы обладают полной симметрией группы Кокстера и представлены двойными незаполненными кольцами, но могут быть представлены и в виде соединений.

Переделанный и голоснубированный

Форма	Символы Шлефли			Симметрия	Диаграмма Кокстера		Пример, {4,3}
Измененный обычный	$a{\begin{Bmatrix}p,q\end{Bmatrix}}$	а{р,q}	в 0 {p,q}	[п, д]	= ∪			Звездчатый октаэдр
Голоснуб двойной обычный	ß{ q , п }	ß{q,p}	в 0,1 {q,p}	[п, д]				Соединение двух икосаэдров

ß , похожая на греческую букву бета (β), является буквой немецкого алфавита eszett .

Полихора и соты

Линейные семьи

Форма	Символ Шлефли			Диаграмма Кокстера		Пример, {4,3,3}
Обычный	${\begin{Bmatrix}p,q,r\end{Bmatrix}}$	{п, д, г}	т 0 {p,q,r}				Тессеракт
Усечено	$t{\begin{Bmatrix}p,q,r\end{Bmatrix}}$	t{p,q,r}	т 0,1 {p,q,r}				Усеченный тессеракт
Исправленный	$\left\{{\begin{array}{l}p\\q,r\end{array}}\right\}$	г {р, q, r}	т 1 {p,q,r}				Исправленный тессеракт	=
Битусеченный		2t{p,q,r}	т 1,2 {p,q,r}				Усеченный тессеракт
биректифицированный (выпрямленный двойной)	$\left\{{\begin{array}{l}q,p\\r\end{array}}\right\}$	2r{p,q,r} = r{r,q,p}	т 2 {p,q,r}				Ректифицированный 16-клеточный	=
Трехусеченный (усеченный двойной)	$t{\begin{Bmatrix}r,q,p\end{Bmatrix}}$	3t{p,q,r} = t{r,q,p}	т 2,3 {p,q,r}				Усеченный тессеракт
Триректифицированный (Двойной)	${\begin{Bmatrix}r,q,p\end{Bmatrix}}$	3r{p,q,r} = {r,q,p}	t 3 {p,q,r} = {r,q,p}				16-ячеечный
Отмененный	$r\left\{{\begin{array}{l}p\\q,r\end{array}}\right\}$	rr{p,q,r}	т 0,2 {p,q,r}				Кантеллированный тессеракт	=
Количество сокращено	$t\left\{{\begin{array}{l}p\\q,r\end{array}}\right\}$	tr{p,q,r}	т 0,1,2 {p,q,r}				Кантитусеченный тессеракт	=
рухлый ( Расширенный )	$e_{3}{\begin{Bmatrix}p,q,r\end{Bmatrix}}$	е 3 {p,q,r}	т 0,3 {p,q,r}				Сморщенный тессеракт
Ранцитусеченный			т 0,1,3 {p,q,r}				Усеченный тессеракт
Всеусеченный			т 0,1,2,3 {p,q,r}				Всеусеченный тессеракт

Чередования, четверти и пренебрежения

Чередования

Форма	Символ Шлефли			Диаграмма Кокстера		Пример, {4,3,3}
Чередования
Половина р даже	$h{\begin{Bmatrix}p,q,r\end{Bmatrix}}$	h{p,q,r}	ht 0 {p,q,r}				16-ячеечный
Четверть п и р даже	$q{\begin{Bmatrix}p,q,r\end{Bmatrix}}$	q{p,q,r}	ht 0 ht 3 {p,q,r}
пренебрежительный q даже	$s{\begin{Bmatrix}p,q,r\end{Bmatrix}}$	s{p,q,r}	ht 0,1 {p,q,r}				Курносый 24-клеточный
Курносый исправлен даже	$s\left\{{\begin{array}{l}p\\q,r\end{array}}\right\}$	ср{p,q,r}	ht 0,1,2 {p,q,r}				Курносый 24-клеточный	=
Чередованная дуопризма		s{p}s{q}	ht 0,1,2,3 {p,2,q}				Великий дуоантипризм

Раздвоенные семьи

Раздвоенные семьи

Форма	Расширенный символ Шлефли			Диаграмма Кокстера		Примеры
Квазирегулярный	$\left\{p,{q \atop q}\right\}$	{p,q 1,1 }	т 0 {p,q 1,1 }				Демитессеракт ( 16-ячеечный )
Усечено	$t\left\{p,{q \atop q}\right\}$	t{p,q 1,1 }	т 0,1 {p,q 1,1 }				Усеченный полудессеракт ( Усеченный 16-клеточный )
Исправленный	$\left\{{\begin{array}{l}p\\q\\q\end{array}}\right\}$	г{р,q 1,1 }	т 1 {p,q 1,1 }				Исправленный полудессеракт ( 24-ячеечный )
Отмененный	$r\left\{{\begin{array}{l}p\\q\\q\end{array}}\right\}$	rr{p,q 1,1 }	т 0,2,3 {p,q 1,1 }				Кантеллированный полудессеракт ( Скошенный 16-клеточный )
Количество сокращено	$t\left\{{\begin{array}{l}p\\q\\q\end{array}}\right\}$	tr{p,q 1,1 }	т 0,1,2,3 {p,q 1,1 }				Кантитусеченный демитессеракт ( Усеченный 16-клеточный )
Курносый исправлен	$s\left\{{\begin{array}{l}p\\q\\q\end{array}}\right\}$	sr{p,q 1,1 }	ht 0,1,2,3 {p,q 1,1 }				Курносый полудессеракт ( Курносый 24-клеточный )
Квазирегулярный	$\left\{r,{p \atop q}\right\}$	{r,/q\,p}	t 0 {r,/q\,p}				Тетраэдрально-октаэдрические соты
Усечено	$t\left\{r,{p \atop q}\right\}$	t{r,/q\,p}	t 0,1 {r,/q\,p}				Усеченные тетраэдрически-октаэдрические соты
Исправленный	$\left\{{\begin{array}{l}r\\p\\q\end{array}}\right\}$	г{r,/q\,p}	t 1 {r,/q\,p}				Выпрямленные тетраэдрически-октаэдрические соты (Ректифицированные кубические соты)
Отмененный	$r\left\{{\begin{array}{l}r\\p\\q\end{array}}\right\}$	rr{r,/q\,p}	t 0,2,3 {r,/q\,p}				Кантелеллированные кубические соты
Количество сокращено	$t\left\{{\begin{array}{l}r\\p\\q\end{array}}\right\}$	tr{r,/q\,p}	т 0,1,2,3 {r,/q\,p}				Канитусеченные кубические соты
Курносый исправлен	$s\left\{{\begin{array}{l}p\\q\\r\end{array}}\right\}$	sr{p,/q,\r}	ht 0,1,2,3 {p,/q\,r}				Курносые выпрямленные кубические соты (неоднородные, но близкие к попаданию)

Мозаика

сферический

• {2,n}
• с{2,2n}
• { } ⊕ {n}

• т{2, п}
• { } + {n}

Обычный

• {2,∞}
• {3,6}

• {4,4}
• {6,3}

Полурегулярный

• с{4,4}
• е{3,6}
• ср{2,∞}
• ср{6,3}
• рр{6,3}

• г{6,3}
• т{6,3}
• т{2,∞}
• тр{6,3}
• тр{4,4}

гиперболический

• ср{5,4}
• ср{6,4}
• ср{7,4}
• ср{8,4}
• ср{∞,4}
• с{5,4}
• ср{6,5}
• с{6,4}
• ср{8,6}
• ср{7,7}
• с{8,4}
• с{4,6}
• ср{∞,∞}
• ср{7,3}
• ср{8,3}
• ср{∞,3}

• с{3,8}
• {3,7}
• {3,8}
• {3,∞}
• ч{8,3}
• ч{6,4}
• д{4,6}
• рр{7,3}
• рр{8,3}
• рр{∞,3}
• ч ₂ {8,3}
• г{7,3}
• г{8,3}
• т{7,3}
• т{8,3}
• г{∞,3}

• т{∞,3}
• рр{5,4}
• рр{6,4}
• рр{7,4}
• рр{8,4}
• рр{∞,4}
• {4,5}
• {4,6}
• {4,7}
• {4,8}
• {4,∞}
• г{5,4}
• г{6,4}
• тр{6,3}
• тр{7,3}
• ???

• тр{8,3}
• ???
• тр{∞,3}
• г{7,4}
• г{8,4}
• тр{5,4}
• ???
• тр{6,4}
• тр{7,4}
• тр{8,4}
• тр{∞,4}
• т{5,4}
• тр{6,5}
• т{6,4}
• тр{8,6}
• т{7,4}

• т{8,4}
• т{∞,4}
• г{∞,4}
• {5,4}
• {5,5}
• {5,6}
• {5,∞}
• рр{6,5}
• г{6,5}
• т{4,5}
• т{5,5}
• т{6,5}
• г{∞,5}
• {6,4}
• {6,5}
• {6,6}

• {6,8}
• рр{8,6}
• г{8,6}
• т{4,6}
• т{5,6}
• т{6,6}
• т{8,6}
• {7,3}
• {7,4}
• {7,7}
• т{3,7}
• т{4,7}
• т{7,7}
• {8,3}
• {8,4}
• {8,6}
• {8,8}

• т{6,8}
• т{3,8}
• т{8,8}
• {∞,3}
• {∞,4}
• {∞,5}
• {∞,∞}
• т{3,∞}
• т{4,∞}

Источники

• Коксетер, Гарольд Скотт Макдональд (1973) [1948]. Правильные многогранники (3-е изд.). Дуврские публикации. стр. 14 , 69, 149. ISBN.  0-486-61480-8 . OCLC   798003 . Правильные многогранники.
• Шерк, Ф. Артур; Макмаллен, Питер; Томпсон, Энтони К.; Вайс, Азия Ивич, ред. (1995). Калейдоскопы: Избранные сочинения HSM Coxeter . Уайли. ISBN  978-0-471-01003-6 .
  • (Документ 22), стр. 251–278. Коксетер, HSM (1940). «Правильные и полуправильные многогранники I». Математика. Зейт . 46 : 380–407. дои : 10.1007/BF01181449 . S2CID   186237114 . Збл   0022.38305 . 2,10 г.р.
  • (Документ 23), стр. 279–312. — (1985). «Правильные и полуправильные многогранники II». Математика. Зейт . 188 (4): 559–591. дои : 10.1007/BF01161657 . S2CID   120429557 . Збл   0547.52005 .
  • (Документ 24), стр. 313–358. — (1988). «Правильные и полуправильные многогранники III». Математика. Зейт . 200 (1): 3–45. дои : 10.1007/BF01161745 . S2CID   186237142 . Збл   0633.52006 .

Внешние ссылки

• Вайсштейн, Эрик В. «Символ Шлефли» . Математический мир . Проверено 28 декабря 2019 г.
• Старк, Морис (13 апреля 2012 г.). «Многогранные имена и обозначения» . Путешествие по миру многогранников . Проверено 28 декабря 2019 г.