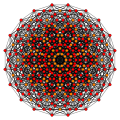
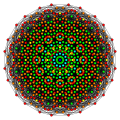
Исправленный тессеракт

Исправленный тессеракт
Диаграмма Шлегеля В центре кубооктаэдра показаны тетраэдрические ячейки
Тип	Равномерный 4-многогранник
Символ Шлефли	г {4,3,3} = $\left\{{\begin{array}{l}4\\3,3\end{array}}\right\}$ 2р{3,3 ^1,1} ч ₃ {4,3,3}
Диаграммы Кокстера-Динкина	=
Клетки	24	8 ( 3.4.3.4 ) 16 ( 3.3.3 )
Лица	88	64 {3} 24 {4}
Края	96
Вершины	32
Вершинная фигура	(Вытянутая равносторонне-треугольная призма)
Группа симметрии	Б ₄ [3,3,4], порядок 384 Д ₄ [3 ^1,1,1], заказ 192
Характеристики	выпуклый , транзитивный по ребру
Единый индекс	10 11 12

В геометрии выпрямленный тессеракт , выпрямленный 8-клеточный — это однородный 4-многогранник (4-мерный многогранник ), ограниченный 24 ячейками : 8 кубооктаэдрами и 16 тетраэдрами . Он имеет половину вершин сморщенного тессеракта , с его конструкция, называемая руническим тессерактом .

Он имеет две однородные конструкции: выпрямленный 8-клеточный r{4,3,3} и кантеллированный демитессеракт rr{3,3. ^1,1}, второй чередуется с двумя типами тетраэдрических ячеек.

Э. Л. Эльте идентифицировал его в 1912 году как полуправильный многогранник, назвав его tC ₈ .

Строительство

Исправленный тессеракт может быть построен из тессеракта путем усечения его вершин в середине его ребер.

Декартовы координаты вершин выпрямленного тессеракта с длиной ребра 2 задаются всеми перестановками:

(0,\ \pm {\sqrt {2}},\ \pm {\sqrt {2}},\ \pm {\sqrt {2}})

Изображения

орфографические проекции
Самолет Коксетера	Б ₄	Б ₃ / Д ₄ / А ₂	Б2 / _Д3
График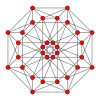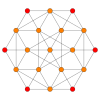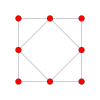
Двугранная симметрия	[8]	[6]	[4]
Самолет Коксетера	F_F4	A_А3
График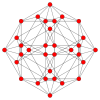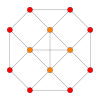
Двугранная симметрия	[12/3]	[4]

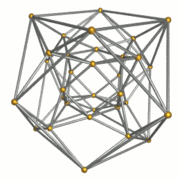Каркас	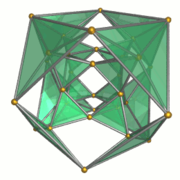16 тетраэдрических ячеек

Прогнозы

В параллельной проекции выпрямленного тессеракта в трехмерное пространство, начиная с кубооктаэдра, изображение имеет следующую компоновку:

Оболочкой проекции является куб .
В этот куб вписан кубооктаэдр, вершины которого лежат в середине ребер куба. Кубооктаэдр — это изображение двух кубооктаэдрических ячеек.
Остальные 6 кубооктаэдрических ячеек проецируются на квадратные грани куба.
8 тетраэдрических объемов, лежащих на треугольных гранях центрального кубооктаэдра, являются изображениями 16 тетраэдрических ячеек, по две ячейки на каждое изображение.

Альтернативные названия

Рит (Джонатан Бауэрс: за исправленный тессеракт)
Амботессеракт ( Нил Слоан и Джон Хортон Конвей )
Исправленный тессеракт / Рунический тессеракт (Норман В. Джонсон)
- 4-гиперкуб Рунчича/8-ячеечный/октахорон/4-мерный многогранник/4-правильный ортотоп
- Выпрямленный 4-гиперкуб/8-клеточный/октахорон/4-мерный многогранник/4-правильный ортотоп

Связанные однородные многогранники

Рунические кубические многогранники

Рунцич n -кубики
n	4	5	6	7	8
[1⁺,4,3^n-2] = [3,3^n-3,1]	[1⁺,4,3²] = [3,3^1,1]	[1⁺,4,3³] = [3,3^2,1]	[1⁺,4,3⁴] = [3,3^3,1]	[1⁺,4,3⁵] = [3,3^4,1]	[1⁺,4,3⁶] = [3,3^5,1]
Runcic figure
Coxeter	=	=	=	=	=
Schläfli	h₃{4,3²}	h₃{4,3³}	h₃{4,3⁴}	h₃{4,3⁵}	h₃{4,3⁶}

Многогранники Тессеракта

Многогранники симметрии B4
Name	tesseract	rectified tesseract	truncated tesseract	cantellated tesseract	runcinated tesseract	bitruncated tesseract	cantitruncated tesseract	runcitruncated tesseract	omnitruncated tesseract
Coxeter diagram		=				=
Schläfli symbol	{4,3,3}	t₁{4,3,3} r{4,3,3}	t_0,1{4,3,3} t{4,3,3}	t_0,2{4,3,3} rr{4,3,3}	t_0,3{4,3,3}	t_1,2{4,3,3} 2t{4,3,3}	t_0,1,2{4,3,3} tr{4,3,3}	t_0,1,3{4,3,3}	t_0,1,2,3{4,3,3}
Schlegel diagram
B₄

Name	16-cell	rectified 16-cell	truncated 16-cell	cantellated 16-cell	runcinated 16-cell	bitruncated 16-cell	cantitruncated 16-cell	runcitruncated 16-cell	omnitruncated 16-cell
Coxeter diagram	=	=	=	=		=	=
Schläfli symbol	{3,3,4}	t₁{3,3,4} r{3,3,4}	t_0,1{3,3,4} t{3,3,4}	t_0,2{3,3,4} rr{3,3,4}	t_0,3{3,3,4}	t_1,2{3,3,4} 2t{3,3,4}	t_0,1,2{3,3,4} tr{3,3,4}	t_0,1,3{3,3,4}	t_0,1,2,3{3,3,4}
Schlegel diagram
B₄

Ссылки

ХСМ Коксетер :
- HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
  - (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
  - (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
Нормана Джонсона Равномерные многогранники , Рукопись (1991)
- Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии. (1966)
2. Выпуклая равномерная полихора на основе тессеракта (8-клеточного) и гексадекахорона (16-клеточного) — Модель 11 , Георгий Ольшевский.
Клитцинг, Ричард. «4D однородные многогранники (полихора) o4x3o3o - rit» .

v т и Фундаментальные выпуклые правильные и однородные многогранники размерностей 2–10.
Семья	н	Б _н	И ₂ (п) / Д _н	Е ₆ / Е ₇ / Е ₈ / Ж ₄ / Г ₂	Ч _н
Правильный многоугольник	Треугольник	Квадрат	п-гон	Шестиугольник	Пентагон
Однородный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный полихорон	Пентахорон	16 ячеек • Тессеракт	Демитессеракт	24-ячеечный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-демикуб
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-демикуб	1 ₂₂ • 2 ₂₁
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-демикуб	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-демикуб	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-демикуб
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-демикуб
Равномерный n - многогранник	n - симплекс	n - ортоплекс • n - куб	n - демикуб	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁	n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений.