9-ортоплекс
| Обычный 9-ортоплекс Эннекросс | |
|---|---|
 Ортогональная проекция внутри многоугольника Петри | |
| Тип | Правильный 9-многогранник |
| Семья | ортоплекс |
| Символ Шлефли | {3 7 ,4} {3 6 ,3 1,1 } |
| Диаграммы Кокстера-Динкина | |
| 8-гранный | 512 {3 7 } |
| 7-гранный | 2304 {3 6 } |
| 6-гранный | 4608 {3 5 } |
| 5-гранный | 5376 {3 4 } |
| 4-ликий | 4032 {3 3 } |
| Клетки | 2016 {3,3} |
| Лица | 672 {3} |
| Края | 144 |
| Вершины | 18 |
| Вершинная фигура | Октакросс |
| Полигон Петри | Октадекагон |
| Группы Кокстера | С 9 , [3 7 ,4] Д 9 , [3 6,1,1 ] |
| Двойной | 9-куб |
| Характеристики | выпуклый многогранник Ханнера |
В геометрии или 9-ортоплекс 9- крестовый многогранник — это правильный 9-многогранник с 18 вершинами , 144 ребрами треугольника , 672 гранями тетраэдра , 2016 ячеек , 4032 5-ячеечными 4-гранями , 5376 5-симплексными 5-гранями , 4608 6-симплексные 6-гранные , 2304 7-симплексные 7-гранные и 512 8-симплексные 8-гранные .
Он имеет две построенные формы, первая из которых регулярная с символом Шлефли {3 7 ,4}, а второй с попеременно помеченными (шахматными) гранями, с символом Шлефли {3 6 ,3 1,1 } или символ Кокстера 6 11 .
Это один из бесконечного семейства многогранников, называемых кросс-многогранниками или ортоплексами . Двойственный многогранник — это 9- гиперкуб или эннеракт .
Альтернативные названия [ править ]
- Эннеакросс , образовано от объединения фамильного крестового многогранника с эннеа, обозначающим девять (измерений) на греческом языке.
- Пентакосидодекайоттон как 512- гранный 9-многогранник (полиоттон)
Строительство [ править ]
Есть две группы Кокстера, связанные с 9-ортоплексом, одна регулярная , двойственная к эннеракту с C 9 или [4,3 7 ] группа симметрии и более низкая симметрия с двумя копиями 8-симплексных фасет, чередующихся, с D 9 или [3 6,1,1 ] группа симметрии.
Декартовы координаты [ править ]
Декартовы координаты вершин 9-ортоплекса с центром в начале координат:
- (±1,0,0,0,0,0,0,0,0), (0,±1,0,0,0,0,0,0,0), (0,0,±1,0,0,0,0,0,0), (0,0,0,±1,0,0,0,0,0), (0,0,0,0,±1,0,0,0,0), (0,0,0,0,0,±1,0,0,0), (0,0,0,0,0,0,±1,0,0), (0,0,0,0,0,0,0,±1,0), (0,0,0,0,0,0,0,0,±1)
Каждая пара вершин соединена ребром , кроме противоположных.
Изображения [ править ]
| BБ9 | Б 8 | Б 7 | |||
|---|---|---|---|---|---|
 |  |  | |||
| [18] | [16] | [14] | |||
| Б 6 | Б 5 | ||||
 | 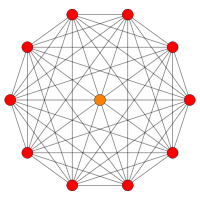 | ||||
| [12] | [10] | ||||
| Б 4 | BБ3 | BБ2 | |||
 |  | 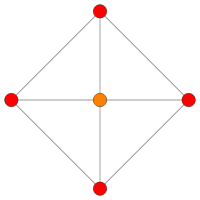 | |||
| [8] | [6] | [4] | |||
| A 7 | AА5 | AА3 | |||
| — | — | — | |||
| [8] | [6] | [4] | |||
Ссылки [ править ]
- ХСМ Коксетер :
- HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
- Нормана Джонсона Равномерные многогранники , Рукопись (1991)
- Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии.
- Клитцинг, Ричард. «9D однородные многогранники (полиотта) x3o3o3o3o3o3o3o4o - ви» .
Внешние ссылки [ править ]
- Ольшевский, Георгий. «Перекрестный многогранник» . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года.
- Многогранники различных размерностей
- Многомерный глоссарий