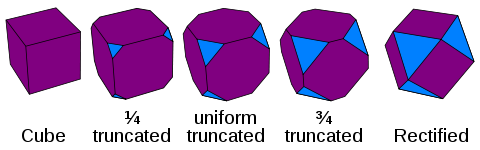
Однородный многогранник

Выпуклые однородные многогранники

2D	3D
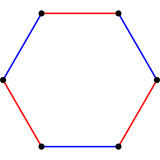Усеченный треугольник или однородный шестиугольник с диаграммой Коксетера 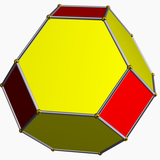.	Усеченный октаэдр ,
4D	5Д
Усеченный 16-клеточный ,	Усеченный 5-ортоплекс ,

В геометрии однородный многогранник размерности три или выше — это вершинно-транзитивный многогранник, ограниченный однородными гранями . Однородные многогранники в двух измерениях — это правильные многоугольники (определение различается в двух измерениях, чтобы исключить вершинно-транзитивные односторонние многоугольники, которые чередуют две разные длины ребер).

Это обобщение более старой категории полуправильных многогранников , но оно также включает и правильные многогранники . Далее звездные правильные грани и вершинные фигуры ( звездные многоугольники допускаются ), что значительно расширяет возможные решения. Строгое определение требует, чтобы однородные многогранники были конечными, в то время как более расширенное определение позволяет однородные соты (двумерные мозаики и соты более высокой размерности ) евклидова и гиперболического пространства также считать многогранниками .

Операции

Почти каждый однородный многогранник может быть создан с помощью конструкции Витхоффа и представлен диаграммой Коксетера . Заметные исключения включают большой диромбикосидодекаэдр в трех измерениях и большую антипризму в четырех измерениях. Терминология для выпуклых однородных многогранников, используемая в однородных многогранниках , однородных 4-многогранниках , однородных 5-многогранниках , однородных 6-многогранниках , однородных мозаиках и выпуклых однородных сотовых изделиях, была придумана Норманом Джонсоном .

Эквивалентно, многогранники Витоффа могут быть созданы путем применения базовых операций к правильным многогранникам в этом измерении. Этот подход был впервые использован Иоганном Кеплером и является основой нотации многогранника Конвея .

Операторы исправления

Правильные n-многогранники имеют n порядков спрямления . Нулевое исправление является исходной формой. ( n −1)-е исправление является двойственным . Выпрямление сводит сводит ребра к вершинам, биректификация сводит грани к вершинам, триректификация ячейки к вершинам, квазиректификация сводит 4-грани к вершинам, квинтректификация сводит 5-граней к вершинам и так далее.

Расширенный символ Шлефли может использоваться для обозначения исправленных форм с одним индексом:

• k -е исправление = t _k {p ₁ , p ₂ , ..., p _n-1 } = k r .

Операторы усечения

Операции усечения, которые можно применять к правильным n -многогранникам в любой комбинации. Полученная диаграмма Кокстера имеет два кольцевых узла, а название операции дано в честь расстояния между ними. Усечение обрезает вершины, кантелляция обрезает ребра, обрезание разрезает грани, стерилизация разрезает ячейки. Каждая более высокая операция также обрезает и более низкие, поэтому свертывание также усекает вершины.

1. t _0,1 или t : Усечение — применяется к полигонам и выше. Усечение удаляет вершины и вставляет новый фасет вместо каждой прежней вершины. Грани усечены, их края удваиваются. (Термин, придуманный Кеплером , происходит от латинского truncare – «отрезать».)

   

   • Существуют также более высокие усечения: побитовое усечение t _1,2 или 2t , тройное усечение t _2,3 или 3t , четырехкратное усечение t _3,4 или 4t , квинтиусечение t _4,5 или 5t и т. д.
2. t _0,2 или rr : Кантелляция – применяется к многогранникам и выше. Это можно рассматривать как исправление своего исправления . Кантелляция усекает как вершины, так и ребра и заменяет их новыми гранями. Клетки заменяются топологически расширенными копиями самих себя. (Термин, придуманный Джонсоном, происходит от глагола «cant» , например, «bevel» , означающего «резать наклонно».)

   

   • Существуют и высшие кантелляции: бикантелляция т _1,3 или r2r , трикантелляция t _2,4 или r3r , квадрикантелляция t _3,5 или r4r и т. д.
   • t _0,1,2 или tr : Кантиусечение — применяется к многогранникам и выше. Это можно рассматривать как усечение его исправления . Кантитрукция усекает как вершины, так и ребра и заменяет их новыми гранями. Клетки заменяются топологически расширенными копиями самих себя. (Композитный термин сочетает в себе кантелляцию и усечение)
     • Существуют также высшие кантелляции: бикантиусушка t _1,2,3 или t2r , трикантиусушка t _2,3,4 или t3r , квадрикантиусушка t _3,4,5 или t4r и т. д.
3. t _0,3 : Ранцинация - применяется к однородным 4-многогранникам и выше. Рансинация усекает вершины, ребра и грани, заменяя каждую из них новыми гранями. 4-лики заменяются топологически расширенными копиями самих себя. (Термин, придуманный Джонсоном, происходит от латинского runcina плотника « плоскость ».)
   • Существуют и более высокие спирали: бирунциация t _1,4 , трирунциация t _2,5 и т. д.
4. t _0,4 или 2r2r : Стерикация – применяется к однородным 5-многогранникам и выше. Его можно рассматривать как двойное исправление своего двойного исправления. Стерификация усекает вершины, ребра, грани и ячейки, заменяя каждую новыми гранями. 5-лики заменяются топологически расширенными копиями самих себя. (Термин, придуманный Джонсоном, происходит от греческого слова «твердый».)
   • Существуют и высшие стерикации: бистерикация т _1,5 или 2р3р , тристерикация т _2,6 или 2р4р и т. д.
   • t _0,2,4 или 2t2r : Стерикантелляция - применяется к однородным 5-многогранникам и выше. Это можно рассматривать как побитовое усечение его биректификации.
     • Существуют и более высокие стерикации: бистерикантелляция т _1,3,5 или 2т3р , тристерикантеллация т _2,4,6 или 2т4р и т. д.
5. t _0,5 : Пентелляция - применяется к однородным 6-многогранникам и выше. Пентелляция усекает вершины, ребра, грани, ячейки и 4-грани, заменяя каждую новыми гранями. Шестигранники заменяются топологически расширенными копиями самих себя. (Пентеляция происходит от греческого pente «пять».)
   • Существуют и высшие пентелляции: бипентелляция т _1,6 , трипентелляция т _2,7 и т. д.
6. t _0,6 или 3r3r : Шестигранник - применяется к однородным 7-многогранникам и выше. Это можно рассматривать как тройное исправление своего тройного исправления. Гексикация усекает вершины, ребра, грани, ячейки, 4- и 5-грани, заменяя каждую новыми гранями. 7-лики заменяются топологически расширенными копиями самих себя. (Гексикация происходит от греческого гекса «шесть».)
   • Существуют также высшие гексикации: бигексикация : т _1,7 или 3р4р , тригексикация : т _2,8 или 3р5р и т. д.
   • t _0,3,6 или 3t3r : Hexiruncinated - применяется к однородным 7-многогранникам и выше. Это можно рассматривать как тройное усечение своего тройного исправления.
     • Существуют также высшие шестигранные: двушестипроволочные : т _1,4,7 или 3т4р , трехшестигранные : т _2,5,8 или 3т5р и т. д.
7. t _0,7 : Гептеллация - применяется к однородным 8-многогранникам и выше. Гептеллация усекает вершины, ребра, грани, ячейки, 4-, 5- и 6-гранные поверхности, заменяя каждую новыми гранями. Восьмигранники заменяются топологически расширенными копиями самих себя. (Гептелляция происходит от греческого hepta «семь».)
   • Существуют и высшие гептелляции: бигептелляция т _1,8 , тригептелляция т _2,9 и т. д.
8. t _0,8 или 4r4r : Октелляция – применяется к однородным 9-многогранникам и выше.
9. t _0,9 : Объединение - применяется к однородным 10-многогранникам и выше.

Кроме того, можно выполнять комбинации усечений, которые также генерируют новые однородные многогранники. Например, прогонка — это прогон и усечение, применяемые вместе.

Если все усечения применяются одновременно, операцию можно в более общем смысле назвать омнитрункацией .

Чередование

Чередование усеченного кубооктаэдра дает курносый куб .

Одна специальная операция, называемая чередованием , удаляет альтернативные вершины из многогранника только с четными гранями. Перемеженный всеусеченный многогранник называется курносым .

Получающиеся в результате многогранники всегда могут быть построены и, как правило, не являются отражающими, а также, как правило, не имеют однородных многогранных решений.

Набор многогранников, образованных чередованием гиперкубов, известен как демикубы . В трех измерениях получается тетраэдр ; в четырех измерениях получается 16-ячеечный или демитессеракт .

Фигура вершины

Однородные многогранники можно построить на основе их фигур вершин , расположения ребер, граней, ячеек и т. д. вокруг каждой вершины. Однородные многогранники, представленные диаграммой Кокстера , обозначающие активные зеркала кольцами, обладают отражательной симметрией и могут быть просто построены путем рекурсивных отражений вершинной фигуры.

Меньшее количество неотражательных однородных многогранников имеют одну фигуру вершины, но не повторяются простыми отражениями. Большинство из них можно представить с помощью таких операций, как чередование других однородных многогранников.

Фигуры вершин для диаграмм Кокстера с одним кольцом можно построить из диаграммы, удалив окольцованный узел и окольцевав соседние узлы. Такие вершинные фигуры сами по себе вершинно-транзитивны.

Многокольцевые многогранники могут быть построены с помощью несколько более сложного процесса построения, и их топология не является однородным многогранником. Например, вершинной фигурой усеченного правильного многогранника (с двумя кольцами) является пирамида. Всеусеченный многогранник (все узлы окольцованы) всегда будет иметь неправильный симплекс в качестве вершинной фигуры.

радиус

Однородные многогранники имеют равные длины ребер, а все вершины находятся на одинаковом расстоянии от центра, называемом радиусом описанной окружности .

Однородные многогранники, радиус описанной окружности которых равен длине ребра, могут использоваться в качестве вершинных фигур для однородных сот . Например, правильный шестиугольник делится на 6 равносторонних треугольников и является вершиной правильной треугольной мозаики . Также кубооктаэдр делится на 8 правильных тетраэдров и 6 квадратных пирамид (полуоктаэдр ) , и это вершинная фигура для чередующихся кубических сот .

Однородные многогранники по размерности

Полезно классифицировать однородные многогранники по размерностям. Это эквивалентно количеству узлов на диаграмме Кокстера или количеству гиперплоскостей в конструкции Витоффа. Поскольку ( n +1)-мерные многогранники являются замощениями n -мерного сферического пространства, замощения n -мерного евклидова и гиперболического пространства также считаются ( n +1)-мерными. Следовательно, мозаики двумерного пространства группируются с трехмерными телами.

Одно измерение

Единственный одномерный многогранник — это отрезок. Он соответствует семейству Кокстера A ₁ .

Два измерения

В двух измерениях существует бесконечное семейство выпуклых однородных многогранников, правильных многоугольников , простейшим из которых является равносторонний треугольник . Усеченные правильные многоугольники становятся двухцветными геометрически квазиправильными многоугольниками с вдвое большим числом сторон, t{p}={2p}. Первые несколько правильных многоугольников (и квазиправильных форм) показаны ниже:

Имя	Треугольник ( 2-симплекс )	Квадрат ( 2-ортоплекс ) ( 2-куб )	Пентагон	Шестиугольник	Семиугольник	Октагон	Девятиугольник	Декагон	Хендекагон
Шлефли	{3}	{4} т{2}	{5}	{6} т{3}	{7}	{8} т{4}	{9}	{10} т{5}	{11}
Коксетер диаграмма
Изображение
Имя	Додекагон	Тридекагон	Тетрадекагон	Пятиугольник	Шестиугольник	Гептадекагон	Октадекагон	Эннеадекагон	Икосагон
Шлефли	{12} т{6}	{13}	{14} т{7}	{15}	{16} т{8}	{17}	{18} т{9}	{19}	{20} т{10}
Коксетер диаграмма
Изображение

Существует также бесконечное множество звездчатых многоугольников (по одному на каждое рациональное число больше 2), но они невыпуклые. Самый простой пример – пентаграмма , которая соответствует рациональному числу 5/2. Правильные звездчатые многоугольники, {p/q}, могут быть усечены в полуправильные звездчатые многоугольники, t{p/q}=t{2p/q}, но становятся двойными покрытиями, если q четно. Усечение также можно выполнить с помощью многоугольника обратной ориентации t{p/(pq)}={2p/(pq)}, например t{5/3}={10/3}.

Имя	Пентаграмма	Гептаграммы		Октаграмма	Эннеаграммы		Декаграмма	... н-аграммы
Шлефли	{5/2}	{7/2}	{7/3}	{8/3} т{4/3}	{9/2}	{9/4}	{10/3} т{5/3}	{ п/к }
Коксетер диаграмма
Изображение

Правильные многоугольники, представленные символом Шлефли {p} для p-угольника. Правильные многоугольники самодвойственны, поэтому в результате выпрямления получается тот же многоугольник. Операция равномерного усечения удваивает стороны до {2p}. Операция сглаживания, чередующаяся с усечением, восстанавливает исходный многоугольник {p}. Таким образом, все однородные многоугольники также являются правильными. Следующие операции можно выполнить над правильными многоугольниками для получения однородных многоугольников, которые также являются правильными многоугольниками:

Операция	Расширенный Шлефли Символы		Обычный результат	Коксетер диаграмма	Позиция		Симметрия
					(1)	(0)
Родитель	{р}	т 0 {р}	{р}		{}	--	[п] (заказать 2р)
Исправленный (Двойной)	г{р}	т 1 {р}	{р}		--	{}	[п] (заказать 2р)
Усечено	т{п}	т 0,1 {р}	{2р}		{}	{}	[[p]]=[2p] (заказать 4р)
Половина	ч{2р}		{р}		--	--	[1 + ,2p]=[p] (заказать 2р)
пренебрежительный	с{п}		{р}		--	--	[[п]] + =[р] (заказать 2р)

Три измерения

Основная статья: Однородный многогранник

В трех измерениях ситуация становится интереснее. Существует пять выпуклых правильных многогранников, известных как Платоновы тела :

Имя	Шлефли {п, д}	Диаграмма	Изображение (прозрачный)	Изображение (твердый)	Изображение (сфера)	Лица {р}	Края	Вершины {q}	Симметрия	Двойной
Тетраэдр ( 3-симплекс ) (Пирамида)	{3,3}					4 {3}	6	4 {3}	Т д	(себя)
Куб ( 3-куб ) (Шестигранник)	{4,3}					6 {4}	12	8 {3}	Ой ​	Октаэдр
Октаэдр ( 3-ортоплекс )	{3,4}					8 {3}	12	6 {4}	Ой ​	Куб
Додекаэдр	{5,3}					12 {5}	30	20 {3}2	I h	Икосаэдр
Икосаэдр	{3,5}					20 {3}	30	12 {5}	I h	Додекаэдр

В дополнение к ним существует также 13 полуправильных многогранников, или архимедовых тел , которые можно получить с помощью конструкций Витхоффа или путем выполнения таких операций, как усечение платоновых тел, как показано в следующей таблице:

	Родитель	Усечено	Исправленный	Битусеченный (тр. двойной)	биректифицированный (двойной)	Отмененный	Всеусеченный ( Количественно усечено )	пренебрежительный
Тетраэдрический 3-3-2	{3,3}	(3.6.6)	(3.3.3.3)	(3.6.6)	{3,3}	(3.4.3.4)	(4.6.6)	(3.3.3.3.3)
Октаэдрический 4-3-2	{4,3}	(3.8.8)	(3.4.3.4)	(4.6.6)	{3,4}	(3.4.4.4)	(4.6.8)	(3.3.3.3.4)
икосаэдрический 5-3-2	{5,3}	(3.10.10)	(3.5.3.5)	(5.6.6)	{3,5}	(3.4.5.4)	(4.6.10)	(3.3.3.3.5)

Существует также бесконечный набор призм , по одной на каждый правильный многоугольник, и соответствующий набор антипризм .

#	Имя	Картина	Укладка плитки	Вертекс фигура	Диаграмма и Шлефли символы
П 2п	Призма				тр{2,р}
п ​	Антипризма				ср{2,р}

К однородным звездчатым многогранникам относятся еще 4 правильных звездчатых многогранника, многогранники Кеплера-Пуансо и 53 полуправильных звездчатых многогранника. Есть также два бесконечных набора: звездные призмы (по одной на каждый звездный многоугольник) и звездные антипризмы (по одной на каждое рациональное число, большее 3/2).

Конструкции

Однородные многогранники и мозаики Витгофа можно определить с помощью их символа Витгофа , который указывает фундаментальную область объекта. Расширение обозначения Шлефли , также используемое Коксетером , применимо ко всем измерениям; он состоит из буквы «t», за которой следует ряд чисел с индексами, соответствующих окольцованным узлам диаграммы Коксетера , и за которым следует символ Шлефли правильного начального многогранника. Например, усеченный октаэдр обозначается обозначением: t _0,1 {3,4}.

Операция	Шлефли Символ			Коксетер диаграмма		Витхофф символ	Позиция:
Родитель	${\begin{Bmatrix}p,q\end{Bmatrix}}$	{п, д}	т 0 {p,q}			д | 2 р	{р}	{ }	--	--	--	{ }
биректифицированный (или двойной )	${\begin{Bmatrix}q,p\end{Bmatrix}}$	{д, р}	т 2 {p,q}			р | 2 кв.	--	{ }	{q}	{ }	--	--
Усечено	$t{\begin{Bmatrix}p,q\end{Bmatrix}}$	t{p,q}	т 0,1 {p,q}			2 кв | п	{2р}	{ }	{q}	--	{ }	{ }
Битусеченный (или усеченный двойной)	$t{\begin{Bmatrix}q,p\end{Bmatrix}}$	т{q,p}	т 1,2 {p,q}			2 р | д	{р}	{ }	{2q}	{ }	{ }	--
Исправленный	${\begin{Bmatrix}p\\q\end{Bmatrix}}$	г {р, q}	т 1 {p,q}			2 | ПК	{р}	--	{q}	--	{ }	--
Отмененный (или расширенный )	$r{\begin{Bmatrix}p\\q\end{Bmatrix}}$	rr{p,q}	т 0,2 {p,q}			ПК | 2	{р}	{ }×{ }	{q}	{ }	--	{ }
Количество сокращено (или всеусеченный )	$t{\begin{Bmatrix}p\\q\end{Bmatrix}}$	tr{p,q}	т 0,1,2 {p,q}			2 кв |	{2р}	{ }×{}	{2q}	{ }	{ }	{ }

Операция	Шлефли Символ			Коксетер диаграмма		Витхофф символ	Позиция:
Курносый исправлен	$s{\begin{Bmatrix}p\\q\end{Bmatrix}}$	ср{п,q}				| 2 шт.	{р}	{3} {3}	{q}	--	--	--
пренебрежительный	$s{\begin{Bmatrix}p,q\end{Bmatrix}}$	с{п,2q}	ht 0,1 {p,q}				с{2п}	{3}	{q}	--	{3}

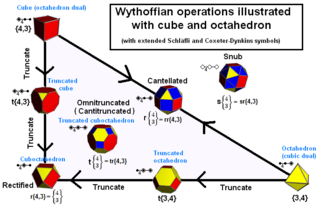Создание треугольников

Четыре измерения

Основная статья: Равномерный 4-многогранник

В четырех измерениях имеется 6 выпуклых правильных 4-многогранников , 17 призм на Платоновых и Архимедовых телах (исключая куб-призму, которую уже посчитали тессерактом ) , и два бесконечных множества: призмы на выпуклых антипризмах, и дуопризмы . Существует также 41 выпуклый полуправильный 4-многогранник, включая невитоффову большую антипризму и курносый 24-клеточный . Оба этих специальных 4-многогранника состоят из подгрупп вершин 600-ячейки .

Не все четырехмерные однородные звездчатые многогранники перечислены. К ним относятся 10 правильных звездчатых (Шлефли-Гесса) 4-многогранников и 57 призм на однородных звездчатых многогранниках, а также три бесконечных семейства: призмы на звездных антипризмах, дуопризмы, образованные перемножением двух звездчатых многоугольников, и дуопризмы, образованные умножением обычного многоугольника на звездчатый многоугольник. Существует неизвестное количество 4-многогранников, не подпадающих под вышеуказанные категории; на данный момент обнаружено более тысячи.

Пример тетраэдра в кубической сотовой ячейке.
Имеется 3 прямых двугранных угла (2 пересекающихся перпендикулярных зеркала):
Ребра 1 к 2, 0 к 2 и 1 к 3.

Сводная диаграмма операций усечения

Каждый правильный многогранник можно рассматривать как изображения фундаментальной области в небольшом количестве зеркал. В 4-мерном многограннике (или 3-мерной кубической соте) фундаментальная область ограничена четырьмя зеркалами. Зеркало в 4-мерном пространстве представляет собой трёхмерную гиперплоскость , но для наших целей удобнее рассматривать только её двумерное пересечение с трёхмерной поверхностью гиперсферы ; таким образом, зеркала образуют неправильный тетраэдр .

Каждый из шестнадцати правильных 4-многогранников порождается одной из четырех групп симметрии следующим образом:

• группа [3,3,3]: 5-ячеечная {3,3,3}, которая является самодвойственной;
• группа [3,3,4]: 16-ячеечная {3,3,4} и ее двойственный тессеракт {4,3,3};
• группа [3,4,3]: 24-клеточный {3,4,3}, самодвойственный;
• группа [3,3,5]: 600-ячеечная {3,3,5}, ее двойная 120-ячеечная {5,3,3} и десять правильных звездочек.
• группа [3 ^1,1,1 ]: содержит только повторяющиеся члены семейства [3,3,4].

(Группы названы в обозначениях Кокстера .)

Восемь выпуклых однородных сот в евклидовом 3-мерном пространстве аналогичным образом генерируются из кубических сот {4,3,4} путем применения тех же операций, которые используются для создания однородных 4-многогранников Витоффа.

Для данного симплекса симметрии образующая точка может быть помещена в любую из четырех вершин, 6 ребер, 4 граней или внутреннего объема. На каждом из этих 15 элементов имеется точка, изображения которой, отраженные в четырех зеркалах, являются вершинами однородного 4-многогранника.

Расширенные символы Шлефли состоят из буквы t, за которой следуют от одного до четырех индексов 0,1,2,3. Если есть один индекс, образующая точка находится в углу фундаментальной области, т. е. в точке, где встречаются три зеркала. Эти углы обозначаются как

• 0 : вершина родительского 4-многогранника (центр двойственной ячейки)
• 1 : центр края родительского элемента (центр грани двойника)
• 2 : центр лица родителя (центр края двойника)
• 3 : центр родительской клетки (вершина двойственной)

(Для двух самодвойственных 4-многогранников «двойной» означает аналогичный 4-многогранник в двойственном положении.) Два или более индексов означают, что образующая точка находится между указанными углами.

Конструктивное резюме

Ниже кратко изложены 15 конструктивных форм по семьям. Самодуальные семейства перечислены в одном столбце, а другие — в двух столбцах с общими записями на симметричных диаграммах Коксетера . В последней 10-й строке перечислены курносые 24-клеточные конструкции. Сюда входят все непризматические однородные 4-многогранники, за исключением невитоффовой большой антипризмы , которая не имеет семейства Кокстера.

A 4	БК 4		Д 4	FF4	Ч 4
[3,3,3]	[4,3,3]		[3,3 1,1 ]	[3,4,3]	[5,3,3]
5-клеточный {3,3,3}	16-ячеечный {3,3,4}	тессеракт {4,3,3}	полудессеракт {3,3 1,1 }	24-ячеечный {3,4,3}	600-ячеечный {3,3,5}	120-ячеечный {5,3,3}
выпрямленный 5-клеточный г {3,3,3}	выпрямленный 16-клеточный г {3,3,4}	исправленный тессеракт г {4,3,3}	исправленный полудессеракт г{3,3 1,1 }	выпрямленный 24-клеточный г {3,4,3}	выпрямленный 600-ячеечный г {3,3,5}	выпрямленный 120-ячеечный г {5,3,3}
усеченный 5-клеточный т{3,3,3}	усеченный 16-ячеечный т{3,3,4}	усеченный тессеракт т{4,3,3}	усеченный полудессеракт т{3,3 1,1 }	усеченный 24-клеточный т{3,4,3}	усеченный 600-ячеечный т{3,3,5}	усеченный 120-ячеечный т{5,3,3}
кантеллированный 5-клеточный рр{3,3,3}	сочлененный 16-клеточный рр{3,3,4}	кантеллированный тессеракт рр{4,3,3}	кантеллированный полудессеракт 2р{3,3 1,1 }	сочлененный 24-клеточный рр{3,4,3}	сочлененный из 600 ячеек рр{3,3,5}	кантеллированный, 120 ячеек рр{5,3,3}
сморщенный 5-клеточный т 0,3 {3,3,3}	сморщенный 16-клеточный т 0,3 {3,3,4}	сморщенный тессеракт т 0,3 {4,3,3}		сморщенный 24-клеточный т 0,3 {3,4,3}	сморщенный 600-клеточный сморщенный 120-клеточный т 0,3 {3,3,5}
усеченный 5-ячеечный т 1,2 {3,3,3}	усеченный 16 ячеек 2т{3,3,4}	усеченный побитно тессеракт 2т{4,3,3}	кантитусеченный полудессеракт 2т{3,3 1,1 }	усеченный 24 ячейки 2т{3,4,3}	усеченный 600 ячеек усеченный 120 ячеек 2т{3,3,5}
кантитусеченный 5-клеточный тр{3,3,3}	усеченный, 16 ячеек тр{3,3,4}	неусеченный тессеракт тр{4,3,3}	всеусеченный полудессеракт тр{3,3 1,1 }	усеченный, 24 ячейки тр{3,4,3}	усеченный, 600 ячеек тр{3,3,5}	усеченный, 120 ячеек тр{5,3,3}
укороченный 5-клеточный т 0,1,3 {3,3,3}	усеченный, 16-клеточный т 0,1,3 {3,3,4}	тессеракт т 0,1,3 {4,3,3}	беглый полудессеракт рр{3,3 1,1 }	усеченный, 24-клеточный т 0,1,3 {3,4,3}	укороченный, 600 ячеек т 0,1,3 {3,3,5}	укороченный, 120 ячеек т 0,1,3 {5,3,3}
всеусеченный 5-клеточный т 0,1,2,3 {3,3,3}	всеусеченный 16-ячеечный т 0,1,2,3 {3,3,4}	всеусеченный тессеракт т 0,1,2,3 {3,3,4}		всеусеченный 24-клеточный т 0,1,2,3 {3,4,3}	всеусеченный, 120-ячеечный всеусеченный на 600 ячеек т 0,1,2,3 {5,3,3}
	чередующиеся кантиусеченные 16-клеточные ср{3,3,4}		пренебрежительный полудессеракт ср{3,3 1,1 }	Чередованный усеченный 24-клеточный с{3,4,3}

Усеченные формы

В следующей таблице определены все 15 форм. Каждое сокращение Форма может иметь от одного до четырех типов ячеек, расположенных в позициях 0,1,2,3, как определено выше. Ячейки помечены многогранными обозначениями усечения.

• -угольная призма n представляется как: {n}×{ }.
• Зеленый фон отображается в формах, которые эквивалентны родительской или двойственной форме.
• Красный фон показывает усечения родительского элемента, а синий — усечения двойного.

Операция	Символ Шлефли		Коксетер диаграмма	Ячейки по положению:
				(3)	(2)	(1)	(0)
Родитель	{п, д, г}	т 0 {p,q,r}		{п, д}	--	--	--
Исправленный	г {р, q, r}	т 1 {p,q,r}		г {р, q}	--	--	{q,r}
биректифицированный (или выпрямленный двойной)	2r{p,q,r} = г{r,q,p}	т 2 {p,q,r}		{д, р}	--	--	г {q, r}
Триректифед (или двойной )	3r{p,q,r} = {г, д, р}	т 3 {p,q,r}		--	--	--	{р, q}
Усечено	t{p,q,r}	т 0,1 {p,q,r}		t{p,q}	--	--	{q,r}
Битусеченный	2t{p,q,r}	2t{p,q,r}		т{q,p}	--	--	т{q,r}
Трехусеченный (или усеченный двойной)	3t{p,q,r} = t{r,q,p}	т 2,3 {p,q,r}		{д, р}	--	--	t{r,q}
Отмененный	rr{p,q,r}	т 0,2 {p,q,r}		rr{p,q}	--	{ }×{r}	г {q, r}
бикантелированный (или согнутый двойной)	r2r{p,q,r} = rr{r,q,p}	т 1,3 {p,q,r}		г {р, q}	{p}×{ }	--	rr{q,r}
рухлый (или расширенный )	е{p,q,r}	т 0,3 {p,q,r}		{п, д}	{p}×{ }	{ }×{r}	{р, q}
Количество сокращено	tr{p,q,r}	tr{p,q,r}		tr{p,q}	--	{ }×{r}	т{q,r}
Бикантиусеченный (или сокращенный двойной)	t2r{p,q,r} = tr{r,q,p}	т 1,2,3 {p,q,r}		т{q,p}	{p}×{ }	--	tr{q,r}
Ранцитусеченный	е т {p,q,r}	т 0,1,3 {p,q,r}		t{p,q}	{2p}×{ }	{ }×{r}	rr{q,r}
Рансикантеллированный (или сокращенный двойной)	е 3t {p,q,r} = е т {r,q,p}	т 0,2,3 {p,q,r}		tr{p,q}	{p}×{ }	{ }×{2r}	t{r,q}
Ранчикантиусеченный (или всеусеченный )	о{p,q,r}	т 0,1,2,3 {p,q,r}		tr{p,q}	{2p}×{ }	{ }×{2r}	tr{q,r}

Полуформы

Полуконструкции существуют с отверстиями, а не с кольцевыми узлами. Ветви, соседние с дырками и неактивными узлами, должны быть четного порядка. Половина конструкции имеет вершины одинаково кольцеобразной конструкции.

Операция	Символ Шлефли		Коксетер диаграмма	Ячейки по положению:
				(3)	(2)	(1)	(0)
Половина Чередование	ч{р,2q,r}	ht 0 {p,2q,r}		ч{р,2q}	--	--	--
Попеременный выпрямленный	час {2p,2q,r}	ht 1 {2p,2q,r}		час{2р,2кв}	--	--	ч{2q,r}
пренебрежительный Попеременное усечение	с{p,2q,r}	ht 0,1 {p,2q,r}		с{п,2q}	--	--	ч{2q,r}
Биснуб Попеременное усечение битов	2s{2p,q,2r}	ht 1,2 {2p,q,2r}		с {q, 2p}	--	--	с {q, 2r}
Курносый исправлен Попеременное усеченное исправленное	ср{p,q,2r}	ht 0,1,2 {p,q,2r}		ср{п,q}	--	с{2,2r}	с {q, 2r}
Омниснуб Попеременное всеусечение	ос{p,q,r}	ht 0,1,2,3 {p,q,r}		ср{п,q}	{p}×{ }	{ }×{r}	ср{q,r}

Пять и более измерений

В пяти и более измерениях существует три правильных многогранника: гиперкуб , симплекс и кросс-многогранник . Они являются обобщениями трехмерного куба, тетраэдра и октаэдра соответственно. В этих размерностях не существует правильных звездчатых многогранников. Большинство однородных многогранников более высокой размерности получаются путем модификации правильных многогранников или путем декартова произведения многогранников более низких размерностей.

, семи и восьми измерениях исключительные группы Ли простые E6 _в , E7 _{В шести} и E8 _{игру вступают} . Помещая кольца на ненулевое количество узлов диаграмм Кокстера , можно получить 39 новых 6-многогранников, 127 новых 7-многогранников и 255 новых 8-многогранников. Ярким примером является 4 ₂₁ многогранник .

Равномерные соты

С темой конечных однородных многогранников связаны однородные соты в евклидовом и гиперболическом пространствах. Евклидовы однородные соты генерируются аффинными группами Кокстера , а гиперболические соты генерируются гиперболическими группами Кокстера . Две аффинные группы Кокстера можно перемножить.

Существует два класса гиперболических групп Кокстера: компактные и паракомпактные. Однородные соты, порожденные компактными группами, имеют конечные грани и фигуры вершин и существуют в измерениях от 2 до 4. Паракомпактные группы имеют аффинные или гиперболические подграфы, бесконечные фасеты или фигуры вершин и существуют в измерениях от 2 до 10.

См. также

• Символ Шлефли

Ссылки

• Коксетер Красота геометрии: двенадцать эссе , Dover Publications, 1999, ISBN   978-0-486-40919-1 (Глава 3: Конструкция Витхоффа для однородных многогранников)
• Нормана Джонсона Равномерные многогранники , Рукопись (1991)
  • Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
• А. Буль Стотт : Геометрический вывод полуправильных многогранников из правильных многогранников и пространственного заполнения , Трактаты о единице ширины Королевской академии наук Амстердам, Первый раздел 11,1, Амстердам, 1910 г.
• ХСМ Коксетер :
  • HSM Коксетер, М. С. Лонге-Хиггинс и Дж. К. П. Миллер: Однородные многогранники , Философские труды Лондонского королевского общества, Лондон, 1954 г.
  • HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
• Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6
  • (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
  • (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
  • (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
• Коксетер , Лонге-Хиггинс, Миллер, Равномерные многогранники , Фил. Пер. 1954, 246 А, 401–50. (Используется расширенное обозначение Шлефли)
• Марко Мёллер, Четырехмерные архимедовы многогранники , диссертация, Гамбургский университет, Гамбург (2004) (на немецком языке)

Внешние ссылки

• Ольшевский, Георгий. «Равномерный многогранник» . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года.
• однородные выпуклые многогранники в четырех измерениях: Марко Мёллер (на немецком языке)