Курносый 24-клеточный
| Курносый 24-клеточный | ||
 | ||
| Тип | Равномерный 4-многогранник | |
| Символ Шлефли [1] | с{3,4,3} ср{3,3,4} с{3 1,1,1 } | |
| Коксетер-Дынкин диаграммы |
| |
| Клетки | 144 | 96 3.3.3 (косой) 24 3.3.3 24 3.3.3.3.3 |
| Лица | 480 {3} | |
| Края | 432 | |
| Вершины | 96 | |
| Вершинная фигура | 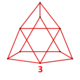 ( Трёхмерный икосаэдр ) | |
| Группы симметрии | [3 + ,4,3] , 1/2 4 F заказ , 576 [(3,3) + ,4] , 1/2 4 B заказ 192 , | |
| Двойной | Двойной курносый 24-элементный | |
| Характеристики | выпуклый | |
| Единый индекс | 30 31 32 | |

8 лиц:


5 3.3.3 и 3 3.3.3.3.3
В геометрии курносый ячеек 24-клеточный или курносый дискоситетрахорон представляет собой выпуклый однородный 4-многогранник, из 120 правильных тетраэдрических и 24 икосаэдрических состоящий . В каждой вершине сходятся пять тетраэдров и три икосаэдра. Всего у него 480 треугольных граней, 432 ребра и 96 вершин. Его можно построить из 600 ячеек, уменьшив выбранное подмножество икосаэдрических пирамид и оставив только их икосаэдрические основания, тем самым удалив 480 тетраэдров и заменив их 24 икосаэдрами.
Топологически, при его высшей симметрии, [3 + ,4,3], как чередование усеченного 24-клеточного , содержит 24 пиритоэдра (икосаэдра с симметрией Th ) , 24 правильных тетраэдра и 96 треугольных пирамид.
Полуправильный многогранник
[ редактировать ]Это один из трех полуправильных 4-многогранников, состоящих из двух или более ячеек, которые являются платоновыми телами , обнаруженных Торольдом Госсетом в его статье 1900 года. [2] Он назвал его тетракосаэдром , поскольку он состоит из тетраэдра и икосаэдра ячеек . (Два других — это исправленный 5-элементный и исправленный 600-элементный .)
Альтернативные названия
[ редактировать ]- Курносый икоситетрахорон
- Курносый полудессеракт
- Полувзносый полиоктаэдр ( Джон Конвей ) [3]
- Сади (Джонатан Бауэрс) за курносый дисикозитрахорон
- Тетрикосаэдрический ( Торольд Госсет ) [2]
Геометрия
[ редактировать ]Координаты
[ редактировать ]Вершины курносого 24-клеточного пространства с центром в начале 4-мерного пространства и ребрами длины 2 получаются четными перестановками
- (0, ±1, ±φ, ±φ 2 )
где φ = 1+ √ 5/2 1,618 ≈ — золотое сечение .
Координаты единичного радиуса курносой 24-клетки с краями длиной φ −1 ≈ 0,618 — четные перестановки
- (± φ / 2 , ± 1 / 2 , ± φ −1 / 2 , 0)
Эти 96 вершин могут быть найдены путем разделения каждого из 96 ребер 24-ячеечного золотого сечения последовательным образом, размерно аналогичным тому, как 12 вершин икосаэдра или «курносого октаэдра» могут быть получены путем разделения 12 ребер. октаэдра в золотом сечении. Это можно сделать, сначала разместив векторы вдоль краев 24 ячеек так, чтобы каждая двумерная грань была ограничена циклом, а затем аналогичным образом разделив каждое ребро на золотое сечение вдоль направления его вектора. [4] Это эквивалентно конструкции усечения с 24 ячейками, описанной ниже.
96 вершин курносой 24-ячейки вместе с 24 вершинами 24-ячейки образуют 120 вершин 600-ячейки .
Конструкции
[ редактировать ]Курносый 24-элементный элемент получается из 24-элементного путем специальной формы усечения .
Усечения удаляют вершины, разрезая ребра, инцидентные вершине; Формы усечения различаются в зависимости от того, где на краю сделан разрез. Обычные усечения 24-клеток включают рецитифицированную 24-клетку (которая разрезает каждое ребро в средней точке, создавая многогранник, ограниченный 24 кубами и 24 кубооктаэдрами ), и усеченную 24-клетку (которая разрезает каждое ребро на одну треть его длину от вершины, образуя многогранник, ограниченный 24 кубами и 24 усеченными октаэдрами ). При этих усечениях на месте удаленной вершины создается куб, поскольку фигура вершины 24-клетки представляет собой куб, а разрезы равноудалены от вершины.
Курносое усечение 24-клеточного [4] разрезает каждое ребро на две золотые секции (так что большая часть находится в золотом пропорции ~ 1,618 к меньшей секции, а исходное ребро находится в золотом пропорции к большей секции). Разрез должен производиться в разных направлениях на разных ребрах, инцидентных каждой вершине, чтобы получить последовательный результат. Ребра, инцидентные вершине в 24-клетке, представляют собой 8 радиусов ее кубической вершинной фигуры. Единственный способ выбрать альтернативные радиусы куба — это выбрать четыре радиуса тетраэдра (вписанного в куб), которые нужно отрезать на меньшем участке их длины от вершины, и четыре противоположных радиуса (другого тетраэдра, который можно вписать в куб), чтобы отрезать большую часть их длины от вершины. Конечно, есть два способа сделать это; оба создают кластер из пяти правильных тетраэдров на месте удаленной вершины, а не куб.
Эта конструкция имеет аналогию в 3-х измерениях: построение икосаэдра (« курносого октаэдра ») из октаэдра тем же методом. [5] Именно так икосаэдры курносых ячеек-24 образуются из октаэдров 24-ячеечных ячеек во время усечения.
Курносый 24-элементный элемент связан с усеченным 24-элементным элементом посредством операции чередования . Половина вершин удаляется, 24 ячейки усеченного октаэдра становятся 24 ячейками икосаэдра , 24 куба становятся 24 ячейками тетраэдра , а 96 удаленных пустот в вершинах создают 96 новых ячеек тетраэдра.
| Курносый 24-клеточный | 600-ячеечный |
|---|---|
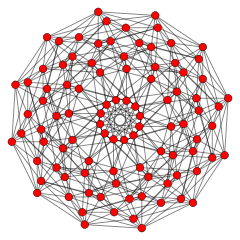 |  |
Курносая 24-ячейка также может быть построена путем особого уменьшения 600 -ячейки : путем удаления 24 вершин из 600-ячейки, соответствующих вершинам вписанной 24-ячейки , а затем взятия выпуклой оболочки оставшихся вершин. Это эквивалентно удалению 24 икосаэдрических пирамид из 600 ячеек.
И наоборот, 600-ячеечную структуру можно построить из курносой 24-ячеечной, дополнив ее 24 икосаэдрическими пирамидами.
Орбиты Вейля
[ редактировать ]Другой метод построения использует кватернионы и икосаэдрическую симметрию орбит группы Вейля . порядка 120. [6] Ниже описаны и 24-ячейки как веса орбит кватернионов D4 под группой Вейля W(D4):
- O(0100) : T = {±1,±e1,±e2,±e3,(±1±e1±e2±e3)/2}
- О(1000): V1
- О (0010): V2
- O(0001) : V3
С кватернионами где является сопряженным и и , то группа Кокстера представляет собой группу симметрии 600-ячеечной и 120-ячеечной ячеек порядка 14400.
Данный такой, что и как обмен в пределах , мы можем построить курносую 24-ячейку как
Структура
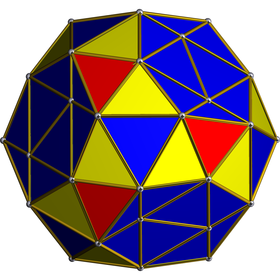
[ редактировать ]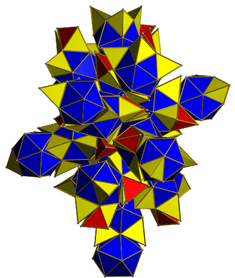 Сетка из курносых 24-клеток с синими икосаэдрами, красными и желтыми тетраэдрами. |
Икосаэдрические ячейки прилегают друг к другу лицом к лицу, оставляя пустоты между ними, заполненные кластерами из пяти тетраэдрических ячеек. [7]
Каждая икосаэдрическая ячейка соединена с 8 другими икосаэдрическими ячейками 8 треугольными гранями в положениях, соответствующих вписывающему октаэдру. Остальные треугольные грани соединены с тетраэдрическими ячейками, которые встречаются парами и имеют общий край икосаэдрической ячейки.
Тетраэдрические клетки можно разделить на две группы: 96 желтых клеток и 24 красных клетки соответственно (как показано на сетке). Каждая желтая тетраэдрическая ячейка соединена своими треугольными гранями с 3 синими икосаэдрическими ячейками и одной красной тетраэдрической клеткой, а каждая красная тетраэдрическая ячейка соединена с 4 желтыми тетраэдрами. Таким образом, тетраэдрические клетки встречаются группами по пять (четыре желтые клетки, соединенные гранями вокруг красной центральной, причем каждая красно-желтая пара лежит в отдельной гиперплоскости). Красный центральный тетраэдр из пяти разделяет каждый из своих шести ребер с другой икосаэдрической ячейкой, а также с парой желтых тетраэдрических ячеек, которые разделяют этот край в икосаэдрической ячейке.
Симметрия
[ редактировать ]Курносая 24-ячейка имеет три вершинно-транзитивных раскраски, основанные на конструкции Витхоффа на группе Кокстера, из которой она чередуется : F 4 определяет 24 взаимозаменяемых икосаэдра, а группа B 4 определяет две группы икосаэдров в соотношении 8:16, и, наконец, группа D 4 имеет 3 группы икосаэдров с числом 8:8:8. [8]
| Симметрия (заказ) | Конструктивное имя | Диаграмма Кокстера-Динкина Расширенный символ Шлефли | Вершинная фигура ( Трёхмерный икосаэдр ) | Клетки (Цвет граней на фигурах вершин) |
|---|---|---|---|---|
| 1 / 2 F 4 [3 + ,4,3] (576) | Курносый 24-клеточный | с{3,4,3} | 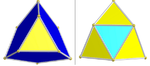 | Один набор из 24 икосаэдров (синего цвета). Два набора тетраэдров: 96 (желтый) и 24 (голубой). |
| 1 / 2 B 4 [(3,3) + ,4] (192) | Курносый выпрямленный 16-кл. | ср{3,3,4} | 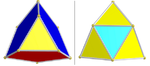 | Два набора икосаэдров: по 8, 16 (красных и синих) Два набора тетраэдров: 96 (желтый) и 24 (голубой). |
| 1 / 2 D 4 [3 1,1,1 ] + (96) | Омниснуб демитессеракт | с{3 1,1,1 } | 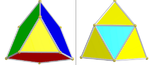 | Три набора по 8 икосаэдров (красный, зеленый и синий). Два набора тетраэдров: 96 (желтый) и 24 (голубой). |
Прогнозы
[ редактировать ]Орфографические проекции
[ редактировать ]| Самолет Коксетера | FF4 | Б 4 |
|---|---|---|
| График |  | 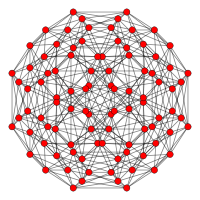 |
| Двугранная симметрия | [12] + | [8/2] |
| Самолет Коксетера | Д 4 / Б 3 / А 2 | Б2 / А3 |
| График | 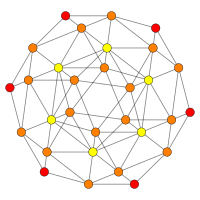 |  |
| Двугранная симметрия | [6] + | [4] |
 Ортогональная проекция Центрирован на гиперплоскости одного икосаэдра. |
Перспективные прогнозы
[ редактировать ]| Перспективные прогнозы | |
|---|---|
 Перспективная проекция с центром в икосаэдрической ячейке с четырехмерной точкой обзора, расположенной на расстоянии, в 5 раз превышающем радиус центра вершины. Ближайшая ячейка икосаэдра отображается сплошным цветом, а остальные ячейки — контуром по краям. Ячейки, обращенные в сторону от точки обзора 4D, удаляются, чтобы уменьшить визуальный беспорядок. | 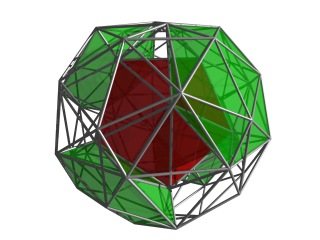 Та же проекция, теперь с 4 из 8 икосаэдрических ячеек, окружающих центральную ячейку, показанную зеленым цветом. |
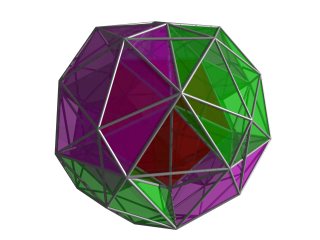 Та же проекция, что и выше, теперь остальные 4 икосаэдрические ячейки, окружающие центральную ячейку, показаны пурпурным цветом. Анимированная версия этого изображения дает хорошее представление о расположении этих ячеек. С этой конкретной точки зрения можно увидеть одну из щелей, содержащую тетраэдрические ячейки. Каждый из этих промежутков заполнен пятью тетраэдрическими ячейками, здесь не показанными. |  Та же проекция, что и выше, теперь с заполненной центральной тетраэдрической ячейкой в промежутке. Эта тетраэдрическая ячейка соединена с четырьмя другими тетраэдрическими ячейками, две из которых заполняют два промежутка, видимые на этом изображении. Два других лежат между зеленой тетраэдрической клеткой, пурпурной клеткой и центральной клеткой слева и справа от желтой тетраэдрической ячейки. Обратите внимание, что на этих изображениях были исключены ячейки, обращенные в сторону от точки обзора 4D; следовательно, здесь учитывается всего 1 + 8 + 6 + 24 = 39 ячеек. Остальные ячейки лежат на другой стороне курносой 24-клетки. Здесь можно различить часть контура края одной из них — икосаэдрической ячейки, перекрывающей желтый тетраэдр. |
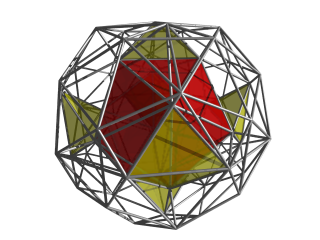 На этом изображении показаны только ближайшая икосаэдрическая ячейка и 6 желтых тетраэдрических ячеек с предыдущего изображения. |  Теперь показаны 12 тетраэдрических ячеек, соединенных с центральной икосаэдрической ячейкой, и 6 желтых тетраэдрических ячеек. Каждая из этих ячеек окружена центральным икосаэдром и двумя другими икосаэдрическими ячейками, показанными ранее. |
 Наконец, здесь показаны остальные 12 тетраэдрических ячеек, присоединенные к 6 желтым тетраэдрическим ячейкам. Эти ячейки вместе с 8 икосаэдрическими ячейками, показанными ранее, включают все ячейки, которые имеют хотя бы одну общую вершину с центральной клеткой. | |
Двойной
[ редактировать ]имеет 24-элементный Dual snub 144 одинаковых элемента неправильной формы. Каждая ячейка имеет грани двух видов: 3 коршуна и 6 равнобедренных треугольников. Всего у многогранника 432 грани (144 змея и 288 равнобедренных треугольников) и 480 ребер. [9]
Связанные многогранники
[ редактировать ]Курносую 24-клетку можно получить убавлением 600-ячейки по 24 ее вершинам, фактически вершинам вписанной 24-клетки . Существует еще такое двууменьшение , когда вершины второй вершины, вписанной в 24 ячейки, также уменьшаются. Соответственно, этот известен как 600-ячеечный би-24-уменьшенный .
| Д 4 равномерная полихора |
|---|
Курносый 24-элементный элемент также называют полукурносым 24-элементным, поскольку он не является настоящим курносым (чередованием всеусеченных 24-элементных элементов). Также можно построить полную курносую 24-ячеечную структуру, хотя она не является однородной и состоит из неправильных тетраэдров с чередующимися вершинами.
Курносые 24-ячеистые соты — это самая большая грань четырехмерных сот, курносые 24-ячеечные соты .
Курносый 24-ячейка является частью F 4 семейства однородных 4-многогранников симметрии .
| 24-клеточные семейные многогранники |
|---|
См. также
[ редактировать ]Цитаты
[ редактировать ]- ^ Клитцинг .
- ^ Jump up to: Перейти обратно: а б Собака 1900 года .
- ^ Конвей, Бургель и Гудман-Штраусс 2008 , стр. 401, 26. Полувзносый полиоктаэдр Госсета.
- ^ Jump up to: Перейти обратно: а б Коксетер 1973 , стр. 151–153, §8.4. Курносый {3,4,3}.
- ^ Коксетер 1973 , стр. 50–52, §3.7.
- ^ Коджа, Аль-Аджми и Оздес Коджа 2011 , стр. 986–988, 6. Двойной курносый 24-клеточный.
- ^ Коджа, Аль-Аджми и Оздес Коджа 2011 , 5. Подробный анализ клеточной структуры курносых 24-клеток.
- ^ Коджа, Оздес Коджа и Аль-Барвани 2012 .
- ^ Коджа, Аль-Аджми и Оздес Коджа 2011 .
Ссылки
[ редактировать ]- Госсет, Торольд (1900). «О правильных и полуправильных фигурах в пространстве n измерений». Вестник математики . Макмиллан.
- Коксетер, HSM (1973) [1948]. Правильные многогранники (3-е изд.). Нью-Йорк: Дувр.
- Конвей, Джон ; Бургель, Хайди; Гудман-Штраус, Хаим (2008). Симметрии вещей . ISBN 978-1-56881-220-5 .
- Коджа, Мехмет; Оздеш Коджа, Назифе; Аль-Барвани, Муатаз (2012). «Крутой 24-клеточный элемент, полученный из группы Кокстера-Вейля W (D4)» . Межд. Дж. Геом. Методы Мод. Физ . 09 (8). arXiv : 1106.3433 . дои : 10.1142/S0219887812500685 . S2CID 119288632 .
- Коджа, Мехмет; Аль-Аджми, Музахир; Оздеш Коджа, Назифе (2011). «Кватернионное представление курносой 24-клетки и ее двойного многогранника, полученного из корневой системы E8» . Линейная алгебра и ее приложения . 434 (4): 977–989. arXiv : 0906.2109 . дои : 10.1016/j.laa.2010.10.005 . ISSN 0024-3795 . S2CID 18278359 .
- Клитцинг, Ричард. «4D однородные многогранники (полихора) s3s4o3o - sadi» .
Внешние ссылки
[ редактировать ]- 3. Выпуклая равномерная полихора на основе икоситетрахора (24-клеточного) — Модель 31 , Георгий Ольшевский.
- Принт №11: Курносая сеть икоситетрахорон , Георгий Ольшевский.
- Курносый икоситетрахорон - Данные и изображения







![{\displaystyle [p,q]:r\rightarrow r'=prq}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a2020e8f2ccdbd85dea0af38e6a0127d5446e42)
![{\displaystyle [p,q]^{*}:r\rightarrow r''=p{\bar {r}}q}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3a23b7f4033871816e91c387a44cf392cac24bd)
![{\displaystyle W(H_{4})=\lbrace [p,{\bar {p}}]\oplus [p,{\bar {p}}]^{*}\rbrace }](https://wikimedia.org/api/rest_v1/media/math/render/svg/13545fc184e7fc37a87f7446d0b9e70bc07cf3b7)

































































