Изогональная фигура

В геометрии многогранник многоугольник (например, или многогранник ) или мозаика является изогональной или вершинно-транзитивной , если все его вершины эквивалентны относительно симметрии фигуры. Это означает, что каждая вершина окружена гранями одного и того же типа в том же или обратном порядке и с одинаковыми углами между соответствующими гранями.

Технически говорят, что для любых двух вершин существует симметрия многогранника, отображающая первую изометрически на вторую. Другими способами это можно сказать, что группа автоморфизмов многогранника действует транзитивно на его вершинах или что вершины лежат внутри одной орбиты симметрии .

Все вершины конечной $n$ -мерной изогональной фигуры существуют на $(n -1)$ -сфере . ^[1]

Термин изогональный издавна использовался для обозначения многогранников. Вершинно-транзитивный — это синоним, заимствованный из современных идей, таких как группы симметрии и теория графов .

Псевдоромбокубооктаэдр , который не является изогональным, демонстрирует, что простое утверждение о том, что «все вершины выглядят одинаково», не так ограничительно, как используемое здесь определение, которое включает группу изометрий, сохраняющих многогранник или мозаику.

Изогональные многоугольники и апейрогоны [ править ]

Изогональные апейрогоны








Изогональные косые апейрогоны

Все правильные многоугольники , апейрогоны и звездчатые многоугольники изогональны . правильные Двойственным изотоксальный изогональному многоугольнику является многоугольник .

Некоторые односторонние многоугольники и апейрогоны , у которых чередуются две длины ребер, например прямоугольник , являются изогональными .

Все плоские изогональные 2 n -угольники имеют двугранную симметрию (D _n , n = 2, 3, ...) с линиями отражения через точки среднего края.

D_Д2	Д ₃	Д ₄	D ₇
Изогональные прямоугольники и скрещенные прямоугольники с одинаковым расположением вершин.	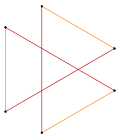Изогональная гексаграмма с 6 одинаковыми вершинами и 2 длинами ребер. ^[2]	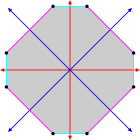Изогональный выпуклый восьмиугольник с синими и красными радиальными линиями отражения	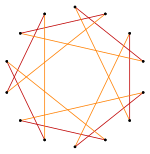Изогональный тетрадекагон «звезда» с одним типом вершин и двумя типами ребер. ^[3]

Изогональные многогранники и двумерные мозаики [ править ]

Изогональные мозаики

Искаженная квадратная плитка

Искаженное усеченная квадратная плитка

Изогональный многогранник и двумерная мозаика имеют вершины одного типа. Изогональный многогранник со всеми правильными гранями также является однородным многогранником и может быть представлен обозначением конфигурации вершин, упорядочивающим грани вокруг каждой вершины. Геометрически искаженным вариантам однородных многогранников и мозаик также можно придать конфигурацию вершин.

Изогональные многогранники
Д _3д , заказать 12	Т _ч , заказ 24	Ох ₄₈ , закажи
4.4.6	3.4.4.4	4.6.8	3.8.8
Искаженная шестиугольная призма (дитригональная трапезопризма)	Искаженный ромбокубооктаэдр.	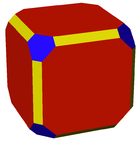Неглубокий усеченный кубооктаэдр	Гиперусеченный куб

Изогональные многогранники и двумерные мозаики можно дополнительно классифицировать:

Правильный , если он также изоэдральный (переходный по граням) и изотоксальный (переходный по ребрам); это означает, что каждая грань представляет собой один и тот же правильный многоугольник .
Квазирегулярный , если он также изотоксичен (транзитивен по ребру), но не изоэдральный (транзитивен по граням).
Полуправильный , если каждая грань представляет собой правильный многоугольник, но не является изоэдральным (транзитивным по граням) или изотоксомальным (транзитивным по ребрам). (Определения различаются у разных авторов; например, некоторые исключают твердые тела с двугранной симметрией или невыпуклые твердые тела.)
Равномерно , если каждая грань является правильным многоугольником, т. е. является правильной, квазиправильной или полуправильной.
Полуоднородный, если его элементы также изогональны.
Чешуйчатая, если все ребра имеют одинаковую длину.
Благородно , если он еще и изоэдральный (гранетранзитивный).

N- : изогональные многогранники и мерности мозаики

более высокой размерности Эти определения могут быть распространены на многогранники и мозаики . Все однородные многогранники изогональны выпуклые , например, однородные 4-многогранники и однородные соты .

Двойственным своих изогональному многограннику является равногранная фигура , транзитивная на гранях .

k -изогональные и k -однородные фигуры [ править ]

Многогранник или мозаику можно назвать k -изогональным , если его вершины образуют k классов транзитивности. Более ограничительный термин, k -uniform, определяется как k-изогональная фигура, построенная только из правильных многоугольников . Их можно визуально представить цветами различных однородных раскрасок .

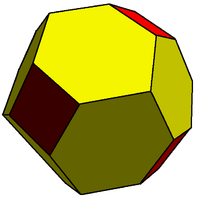Этот усеченный ромбдодекаэдр является 2-изогональным, поскольку содержит два класса транзитивности вершин. Этот многогранник состоит из квадратов и сплющенных шестиугольников .	Это полурегулярное замощение также 2-изогонально (и 2-равномерно ). Эта мозаика состоит из равностороннего треугольника и правильных шестиугольных граней.	2-изогональная эннеаграмма 9/4 (грань конечной звездчатости икосаэдра )

См. также [ править ]

Край-транзитивный (изотоксальная фигура)
Грань-переходная (Изоэдральная фигура)

Ссылки [ править ]

^ Грюнбаум, Бранко (1997), «Изогональные призматоиды», Дискретная и вычислительная геометрия , 18 (1): 13–52, doi : 10.1007/PL00009307 , MR 1453440
^ Коксетер, Плотности правильных многогранников II, стр. 54-55, вершинная фигура «гексаграммы» h {5/2,5}.
^ Светлая сторона математики: материалы конференции памяти Эжена Стренса по развлекательной математике и ее истории , (1994), Метаморфозы многоугольников , Бранко Грюнбаум , Рисунок 1. Параметр t = 2,0

Питер Р. Кромвель, Многогранники , Издательство Кембриджского университета, 1997, ISBN 0-521-55432-2 , с. 369 Транзитивность
Грюнбаум, Бранко ; Шепард, GC (1987). Плитки и узоры . WH Фриман и компания. ISBN 0-7167-1193-1 . (стр. 33 k-изогональные мозаики, стр. 65 k-равномерные мозаики )

Внешние ссылки [ править ]

Вайсштейн, Эрик В. «Вершинно-транзитивный граф» . Математический мир .
Изогональные калейдоскопические многогранники Владимир Л. Булатов , физический факультет, Университет штата Орегон, Корваллис, представлено на Mosaic2000, Открытом симпозиуме тысячелетия по искусству и междисциплинарным вычислениям, 21–24 августа 2000 г., Сиэтл, Вашингтон, модели VRML
Стивен Датч использует термин k-равномерный для перечисления k-изогональных мозаик.
Список n-однородных мозаик
Вайсштейн, Эрик В. «Демирегулярные мозаики» . Математический мир . (Также используется термин k-равномерный для k-изогонального)

[1] Грюнбаум, Бранко (1997), «Изогональные призматоиды», Дискретная и вычислительная геометрия , 18 (1): 13–52, doi : 10.1007/PL00009307 , MR 1453440

[2] Коксетер, Плотности правильных многогранников II, стр. 54-55, вершинная фигура «гексаграммы» h {5/2,5}.

[3] Светлая сторона математики: материалы конференции памяти Эжена Стренса по развлекательной математике и ее истории , (1994), Метаморфозы многоугольников , Бранко Грюнбаум , Рисунок 1. Параметр t = 2,0

[1]

[2]

[3]