Двугранный угол

— Двугранный угол это угол между двумя пересекающимися плоскостями или полуплоскостями . В химии это угол по часовой стрелке между полуплоскостями двух наборов по три атома , имеющих два общих атома. В твердотельной геометрии это определяется как объединение прямой общим и двух полуплоскостей, у которых эта линия является краем . В более высоких измерениях двугранный угол представляет собой угол между двумя гиперплоскостями . Говорят, что плоскости летательного аппарата находятся под положительным двугранным углом, когда основные плоскости как правого, так и левого борта (обычно называемые «крыльями») наклонены вверх к боковой оси; когда они наклонены вниз, говорят, что они находятся под отрицательным двугранным углом.

Математическая основа [ править ]

Когда две пересекающиеся плоскости описываются в декартовых координатах двумя уравнениями

a_{1}x+b_{1}y+c_{1}z+d_{1}=0

a_{2}x+b_{2}y+c_{2}z+d_{2}=0

двугранный угол, $\varphi$ между ними определяется:

\cos \varphi ={\frac {\left\vert a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}\right\vert }{{\sqrt {a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}}{\sqrt {a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}}}

и удовлетворяет $0\leq \varphi \leq \pi /2.$ Легко заметить, что угол не зависит от $d_{1}$ и $d_{2}$ .

В качестве альтернативы, если $n A$ и $n B$ являются векторами нормалей к плоскостям, имеем

\cos \varphi ={\frac {\left\vert \mathbf {n} _{\mathrm {A} }\cdot \mathbf {n} _{\mathrm {B} }\right\vert }{|\mathbf {n} _{\mathrm {A} }||\mathbf {n} _{\mathrm {B} }|}}

где $n A \cdot n B$ — скалярное произведение векторов и $| п А | | п Б |$ является произведением их длин. ^[1]

В приведенных выше формулах требуется абсолютное значение, поскольку плоскости не изменяются при изменении знаков всех коэффициентов в одном уравнении или замене одного нормального вектора его противоположным.

Однако абсолютных значений можно и следует избегать при рассмотрении двугранного угла двух полуплоскостей , границы которых представляют собой одну и ту же линию. В этом случае полуплоскости можно описать точкой $P$ их пересечения и тремя векторами $b 0$ , $b 1$ и $b 2$ такими, что $P + b 0$ , $P + b 1$ и $P + b 2$ принадлежат соответственно пересечению линия, первая полуплоскость и вторая полуплоскость. Двугранный угол этих двух полуплоскостей определяется выражением

\cos \varphi ={\frac {(\mathbf {b} _{0}\times \mathbf {b} _{1})\cdot (\mathbf {b} _{0}\times \mathbf {b} _{2})}{|\mathbf {b} _{0}\times \mathbf {b} _{1}||\mathbf {b} _{0}\times \mathbf {b} _{2}|}}

,

и удовлетворяет $0\leq \varphi <\pi .$ В этом случае переключение двух полуплоскостей дает тот же результат, как и замена $\mathbf {b} _{0}$ с $-\mathbf {b} _{0}.$ В химии (см. ниже) мы определяем двугранный угол так, что заменяя $\mathbf {b} _{0}$ с $-\mathbf {b} _{0}$ меняет знак угла, который может находиться в пределах от $- π$ до $π$ .

В физике полимеров [ править ]

В некоторых научных областях, таких как физика полимеров , можно рассматривать цепочку точек и связи между последовательными точками. Если точки последовательно пронумерованы и расположены в позициях $r 1$ , $r 2$ , $r 3$ и т. д., то векторы связей определяются формулами $u 1$ = $r 2$ - $r 1$ , $u 2$ = $r 3$ - $r 2$ и $u i$ = $r i+1$ − $r i$ , в более общем плане. ^[2]Это относится к кинематическим цепям или аминокислотам в структуре белка . В этих случаях часто интересуют полуплоскости, определяемые тремя последовательными точками, и двугранный угол между двумя последовательными такими полуплоскостями. Если $u 1$ , $u 2$ и $u 3$ — три последовательных вектора связи, пересечение полуплоскостей ориентировано, что позволяет определить двугранный угол, принадлежащий интервалу $(- π, π]$ . Этот двугранный угол определяется выражением ^[3]

{\begin{aligned}\cos \varphi &={\frac {(\mathbf {u} _{1}\times \mathbf {u} _{2})\cdot (\mathbf {u} _{2}\times \mathbf {u} _{3})}{|\mathbf {u} _{1}\times \mathbf {u} _{2}|\,|\mathbf {u} _{2}\times \mathbf {u} _{3}|}}\\\sin \varphi &={\frac {\mathbf {u} _{2}\cdot ((\mathbf {u} _{1}\times \mathbf {u} _{2})\times (\mathbf {u} _{2}\times \mathbf {u} _{3}))}{|\mathbf {u} _{2}|\,|\mathbf {u} _{1}\times \mathbf {u} _{2}|\,|\mathbf {u} _{2}\times \mathbf {u} _{3}|}},\end{aligned}}

или, используя функцию atan2 ,

\varphi =\operatorname {atan2} (\mathbf {u} _{2}\cdot ((\mathbf {u} _{1}\times \mathbf {u} _{2})\times (\mathbf {u} _{2}\times \mathbf {u} _{3})),|\mathbf {u} _{2}|\,(\mathbf {u} _{1}\times \mathbf {u} _{2})\cdot (\mathbf {u} _{2}\times \mathbf {u} _{3})).

Этот двугранный угол не зависит от ориентации цепочки (порядка, в котором рассматриваются точки) — обращение этого порядка состоит в замене каждого вектора противоположным ему вектором и замене индексов 1 и 3. Обе операции не меняют косинус , но поменяйте знак синуса. Таким образом, вместе они не меняют угол.

Более простая формула для того же двугранного угла следующая (доказательство приведено ниже):

{\begin{aligned}\cos \varphi &={\frac {(\mathbf {u} _{1}\times \mathbf {u} _{2})\cdot (\mathbf {u} _{2}\times \mathbf {u} _{3})}{|\mathbf {u} _{1}\times \mathbf {u} _{2}|\,|\mathbf {u} _{2}\times \mathbf {u} _{3}|}}\\\sin \varphi &={\frac {|\mathbf {u} _{2}|\,\mathbf {u} _{1}\cdot (\mathbf {u} _{2}\times \mathbf {u} _{3})}{|\mathbf {u} _{1}\times \mathbf {u} _{2}|\,|\mathbf {u} _{2}\times \mathbf {u} _{3}|}},\end{aligned}}

или эквивалентно,

\varphi =\operatorname {atan2} (|\mathbf {u} _{2}|\,\mathbf {u} _{1}\cdot (\mathbf {u} _{2}\times \mathbf {u} _{3}),(\mathbf {u} _{1}\times \mathbf {u} _{2})\cdot (\mathbf {u} _{2}\times \mathbf {u} _{3})).

Это можно вывести из предыдущих формул, используя формулу векторного четырехкратного произведения и тот факт, что скалярное тройное произведение равно нулю, если оно содержит дважды один и тот же вектор:

(\mathbf {u} _{1}\times \mathbf {u} _{2})\times (\mathbf {u} _{2}\times \mathbf {u} _{3})=[(\mathbf {u} _{2}\times \mathbf {u} _{3})\cdot \mathbf {u} _{1}]\mathbf {u} _{2}-[(\mathbf {u} _{2}\times \mathbf {u} _{3})\cdot \mathbf {u} _{2}]\mathbf {u} _{1}=[(\mathbf {u} _{2}\times \mathbf {u} _{3})\cdot \mathbf {u} _{1}]\mathbf {u} _{2}

Учитывая определение векторного произведения , это означает, что $\varphi$ - это угол четвертого атома по часовой стрелке по сравнению с первым атомом, если смотреть вниз по оси от второго атома к третьему. Особыми случаями (можно сказать обычными) являются $\varphi =\pi$ , $\varphi =+\pi /3$ и $\varphi =-\pi /3$ , которые называются транс , гош ⁺и грубый ⁻ конформации.

В стереохимии [ править ]


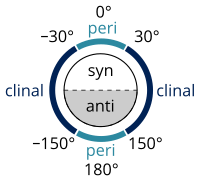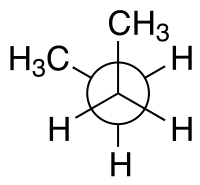Имена конфигураций по двугранному углу	син -н- бутан в ЛЕВЫЙ ⁻ конформация (-60°) Проекция Ньюмана	син -н- бутан козла проекция

В стереохимии торсионный угол определяется как частный пример двугранного угла, описывающего геометрическое соотношение двух частей молекулы, соединенных химической связью . ^[4]^[5]Каждый набор из трех неколлинеарных атомов молекулы определяет полуплоскость. Как объяснялось выше, когда две такие полуплоскости пересекаются (т. е. набор из четырех последовательно связанных атомов), угол между ними представляет собой двугранный угол. Двугранные углы используются для определения молекулярной конформации . ^[6] Стереохимические структуры, соответствующие углам от 0 ° до ± 90 °, называются син (s), а те, которые соответствуют углам от ± 90 ° до 180 °, анти (а). Точно так же расположения, соответствующие углам между 30 ° и 150 ° или между -30 ° и -150 °, называются клинальными (c), а расположения между 0 ° и ± 30 ° или ± 150 ° и 180 ° называются перипланарными (p).

Эти два типа терминов можно объединить, чтобы определить четыре диапазона углов; от 0° до ±30° синперипланарно (sp); синклинальные от 30° до 90° и от -30° до -90° (sc); антиклиналь от 90° до 150° и от -90° до -150° (переменный ток); ±150–180° антиперипланарно (ap). Синперипланарная конформация также известна как син- или цис -конформация; антиперипланарный как анти или транс ; и синклинальный, как неуклюжий или перекошенный .

Например, для н - бутана две плоскости могут быть определены через два центральных атома углерода и один из атомов углерода метила. Показанная выше син - конформация с двугранным углом 60° менее стабильна, чем анти -конформация с двугранным углом 180°.

Для макромолекулярного использования символы T, C, G ⁺, Г ⁻, А ⁺ и А ⁻ рекомендуются (ap, sp, +sc, -sc, +ac и -ac соответственно).

Белки [ править ]

График Рамачандрана (также известный как диаграмма Рамачандрана или график [ φ , ψ ]), первоначально разработанный в 1963 году Г. Н. Рамачандраном , К. Рамакришнаном и В. Сасисекхараном. ^[7]- это способ визуализировать энергетически разрешенные области для двугранных углов ψ зависимости от φ аминокислотных основной цепи в остатков в структуре белка . В белковой цепи определяются три двугранных угла:

ω (омега) – угол в цепочке C ^а - С' - Н - С ^а,
φ(phi) — угол в цепочке C' − N − C ^а − С'
ψ (psi) — угол в цепочке N − C ^а − C' − N (названный φ′ ) Рамачандраном

Рисунок справа иллюстрирует расположение каждого из этих углов (но неправильно показывает, как они определяются). ^[8]

Планарность пептидной связи обычно ограничивает ω значением 180° (типичный транс- случай) или 0° (редкий цис- случай). Расстояние между С ^аатомов в транс- и цис -изомерах составляет примерно 3,8 и 2,9 Å соответственно. Подавляющее большинство пептидных связей в белках являются транс- , хотя в пептидной связи с азотом пролина преобладает цис-связь по сравнению с другими парами аминокислот. ^[9]

Двугранные углы боковой цепи обозначены χ _n (chi- n ). ^[10] Они имеют тенденцию группироваться около 180 °, 60 ° и -60 °, которые называются транс , гош . ⁻и грубый ⁺конформации. На стабильность некоторых двугранных углов боковой цепи влияют значения φ и ψ . ^[11] Например, существуют прямые стерические взаимодействия между C γ боковой цепи в гош ⁺ ротамер и азот основной цепи следующего остатка, когда ψ около -60°. ^[12] Это очевидно из статистических распределений в зависимых от основной цепи библиотеках ротамеров .

Преобразование двугранных углов в декартовы координаты в цепочках [ править ]

Основы полимеров, особенно белков, принято представлять во внутренних координатах ; то есть список последовательных двугранных углов и длин связей. Однако в некоторых видах вычислительной химии вместо этого используются декартовы координаты . При оптимизации вычислительной структуры некоторым программам необходимо переключаться между этими представлениями во время своих итераций. Эта задача может доминировать над временем расчета. Для процессов со многими итерациями или длинными цепочками это также может привести к накопленной числовой неточности. Хотя все алгоритмы преобразования дают математически идентичные результаты, они различаются по скорости и числовой точности. ^[13]^{[ нужен неосновной источник ]}

Геометрия [ править ]

Каждый многогранник имеет двугранный угол на каждом ребре, описывающий взаимосвязь двух граней, разделяющих это ребро. Этот двугранный угол, также называемый углом грани , измеряется как внутренний угол по отношению к многограннику. Угол 0° означает, что векторы нормалей граней антипараллельны и грани перекрывают друг друга, что означает, что они являются частью вырожденного многогранника. Угол 180° означает, что грани параллельны, как в мозаике . Угол больше 180° существует на вогнутых частях многогранника.

Каждый двугранный угол в реберно-транзитивном многограннике имеет одно и то же значение. Сюда входят 5 платоновых тел , 13 каталанских тел , 4 многогранника Кеплера-Пуансо , два квазирегулярных тела и два квазирегулярных двойственных тела.

Закон косинусов для двугранного угла [ править ]

Учитывая три грани многогранника, которые встречаются в общей вершине P и имеют ребра AP, BP и CP, косинус двугранного угла между гранями, содержащими APC и BPC, равен: ^[14]

\cos \varphi ={\frac {\cos(\angle \mathrm {APB} )-\cos(\angle \mathrm {APC} )\cos(\angle \mathrm {BPC} )}{\sin(\angle \mathrm {APC} )\sin(\angle \mathrm {BPC} )}}

Это можно вывести из сферического закона косинусов.

См. также [ править ]

атропоизомер

Ссылки [ править ]

^ «Угол между двумя плоскостями» . TutorVista.com . Архивировано из оригинала 28 октября 2020 г. Проверено 6 июля 2018 г.
^ Крегер, Мартин (2005). Модели полимерных и анизотропных жидкостей . Спрингер. ISBN 3540262105 .
^ Блондель, Арно; Карплюс, Мартин (7 декабря 1998 г.). «Новая формулировка производных торсионных углов и несобственных торсионных углов в молекулярной механике: устранение особенностей». Журнал вычислительной химии . 17 (9): 1132–1141. doi : 10.1002/(SICI)1096-987X(19960715)17:9<1132::AID-JCC5>3.0.CO;2-T .
^ ИЮПАК , Сборник химической терминологии , 2-е изд. («Золотая книга») (1997). Интернет-исправленная версия: (2006–) « Угол кручения ». два : 10.1351/goldbook.T06406
^ ИЮПАК , Сборник химической терминологии , 2-е изд. («Золотая книга») (1997). Онлайн исправленная версия: (2006–) « Двугранный угол ». дои : 10.1351/goldbook.D01730
^ Анслин, Эрик; Деннис Догерти (2006). Современная физико-органическая химия . Университетская наука. п. 95. ИСБН 978-1891389313 .
^ Рамачандран, Дж.Н.; Рамакришнан, К.; Сасисекхаран, В. (1963). «Стереохимия конфигураций полипептидных цепей». Журнал молекулярной биологии . 7 : 95–9. дои : 10.1016/S0022-2836(63)80023-6 . ПМИД 13990617 .
^ Ричардсон, Дж. С. (1981). «Анатомия и таксономия структуры белка». Анатомия и систематика белковых структур . Достижения в химии белков. Том. 34. стр. 167–339. дои : 10.1016/S0065-3233(08)60520-3 . ISBN 9780120342341 . ПМИД 7020376 .
^ Сингх Дж., Хансон Дж., Хеффернан Р., Паливал К., Ян Ю., Чжоу Ю. (август 2018 г.). «Обнаружение цис-изомеров пролина и непролина в белковых структурах по последовательностям с использованием глубокого обучения остаточного ансамбля». Журнал химической информации и моделирования . 58 (9): 2033–2042. doi : 10.1021/acs.jcim.8b00442 . ПМИД 30118602 . S2CID 52031431 .
^ «Конформация боковой цепи» .
^ Данбрэк, Р.Л. младший; Карплюс, М. (20 марта 1993 г.). «Основно-зависимая библиотека ротамеров для белков. Применение для предсказания боковой цепи». Журнал молекулярной биологии . 230 (2): 543–74. дои : 10.1006/jmbi.1993.1170 . ПМИД 8464064 .
^ Данбрек, Р.Л. младший; Карплюс, М. (май 1994 г.). «Конформационный анализ зависимых от основной цепи предпочтений ротамеров боковых цепей белка». Структурная биология природы . 1 (5): 334–40. дои : 10.1038/nsb0594-334 . ПМИД 7664040 . S2CID 9157373 .
^ Парсонс, Дж.; Холмс, Дж. Б.; Рохас, Дж. М.; Цай, Дж.; Штраус, CE (2005), «Практическое преобразование торсионного пространства в декартово пространство для синтеза белка in silico», Journal of Computational Chemistry , 26 (10): 1063–1068, doi : 10.1002/jcc.20237 , PMID 15898109 , S2CID 2279574
^ «калькулятор двугранных углов многогранника» . www.had2know.com . Архивировано из оригинала 25 ноября 2015 года . Проверено 25 октября 2015 г.

Внешние ссылки [ править ]

Двугранный угол в деревообработке на Tips.FM
Анализ пяти правильных многогранников дает пошаговый вывод этих точных значений.

[1] «Угол между двумя плоскостями» . TutorVista.com . Архивировано из оригинала 28 октября 2020 г. Проверено 6 июля 2018 г.

[kroger-2] Крегер, Мартин (2005). Модели полимерных и анизотропных жидкостей . Спрингер. ISBN 3540262105 .

[3] Блондель, Арно; Карплюс, Мартин (7 декабря 1998 г.). «Новая формулировка производных торсионных углов и несобственных торсионных углов в молекулярной механике: устранение особенностей». Журнал вычислительной химии . 17 (9): 1132–1141. doi : 10.1002/(SICI)1096-987X(19960715)17:9<1132::AID-JCC5>3.0.CO;2-T .

[4] ИЮПАК , Сборник химической терминологии , 2-е изд. («Золотая книга») (1997). Интернет-исправленная версия: (2006–) « Угол кручения ». два : 10.1351/goldbook.T06406

[5] ИЮПАК , Сборник химической терминологии , 2-е изд. («Золотая книга») (1997). Онлайн исправленная версия: (2006–) « Двугранный угол ». дои : 10.1351/goldbook.D01730

[dougherty-6] Анслин, Эрик; Деннис Догерти (2006). Современная физико-органическая химия . Университетская наука. п. 95. ИСБН 978-1891389313 .

[7] Рамачандран, Дж.Н.; Рамакришнан, К.; Сасисекхаран, В. (1963). «Стереохимия конфигураций полипептидных цепей». Журнал молекулярной биологии . 7 : 95–9. дои : 10.1016/S0022-2836(63)80023-6 . ПМИД 13990617 .

[8] Ричардсон, Дж. С. (1981). «Анатомия и таксономия структуры белка». Анатомия и систематика белковых структур . Достижения в химии белков. Том. 34. стр. 167–339. дои : 10.1016/S0065-3233(08)60520-3 . ISBN 9780120342341 . ПМИД 7020376 .

[9] Сингх Дж., Хансон Дж., Хеффернан Р., Паливал К., Ян Ю., Чжоу Ю. (август 2018 г.). «Обнаружение цис-изомеров пролина и непролина в белковых структурах по последовательностям с использованием глубокого обучения остаточного ансамбля». Журнал химической информации и моделирования . 58 (9): 2033–2042. doi : 10.1021/acs.jcim.8b00442 . ПМИД 30118602 . S2CID 52031431 .

[10] «Конформация боковой цепи» .

[11] Данбрэк, Р.Л. младший; Карплюс, М. (20 марта 1993 г.). «Основно-зависимая библиотека ротамеров для белков. Применение для предсказания боковой цепи». Журнал молекулярной биологии . 230 (2): 543–74. дои : 10.1006/jmbi.1993.1170 . ПМИД 8464064 .

[12] Данбрек, Р.Л. младший; Карплюс, М. (май 1994 г.). «Конформационный анализ зависимых от основной цепи предпочтений ротамеров боковых цепей белка». Структурная биология природы . 1 (5): 334–40. дои : 10.1038/nsb0594-334 . ПМИД 7664040 . S2CID 9157373 .

[NERF-13] Парсонс, Дж.; Холмс, Дж. Б.; Рохас, Дж. М.; Цай, Дж.; Штраус, CE (2005), «Практическое преобразование торсионного пространства в декартово пространство для синтеза белка in silico», Journal of Computational Chemistry , 26 (10): 1063–1068, doi : 10.1002/jcc.20237 , PMID 15898109 , S2CID 2279574

[14] «калькулятор двугранных углов многогранника» . www.had2know.com . Архивировано из оригинала 25 ноября 2015 года . Проверено 25 октября 2015 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]