Каталонский солид

Триакис тетраэдр , пятиугольный икоситетраэдр и дисдиакис триаконтаэдр .

Сплошные тела выше (темные) показаны вместе с их двойниками (светлыми). Видимые части каталонских тел представляют собой правильные пирамиды .

Ромбический додекаэдр с конфигурацией граней .

В математике , каталонское тело или двойственное к Архимеду тело , представляет собой многогранник, двойственный телу архимедову . Всего каталонских тел 13. Они названы в честь бельгийского математика Эжена Каталана , впервые описавшего их в 1865 году.

Все каталонские тела выпуклые . Они гране-транзитивны , но не вершинно-транзитивны . Это связано с тем, что двойственные архимедовы тела являются вершинно-транзитивными, а не гране-транзитивными. Обратите внимание, что в отличие от платоновых тел и тел Архимеда , грани каталонских тел не являются правильными многоугольниками . Однако вершинные фигуры каталонских тел правильные и имеют постоянные двугранные углы . Будучи транзитивными по граням, каталонские тела представляют собой изоэдры .

Кроме того, два каталонских тела являются транзитивными по ребрам : ромбический додекаэдр и ромбический триаконтаэдр . Это двойники двух квазирегулярных архимедовых тел.

Точно так же, как призмы и антипризмы обычно не считаются архимедовыми телами, бипирамиды и трапецоэдры обычно не считаются каталонскими телами, несмотря на то, что они транзитивны по граням.

Два из каталонских тел являются хиральными : пятиугольный икоситетраэдр и пятиугольный гексеконтаэдр , двойственный киральному курносому кубу и курносому додекаэдру . Каждый из них бывает двух энантиоморфов . Не считая энантиоморф, бипирамид и трапецоэдров, всего каталонских тел 13.

Одиннадцать из 13 каталонских тел обладают свойством Руперта : копию тела той же или большей формы можно пропустить через отверстие в твердом теле.

Список каталонских тел и их двойников

Имя Конвея	Архимедово двойственное	Лицо многоугольник	Ортогональный каркасы	Картинки	Углы грани (°)	Двугранный угол (°)	Мидрадиус	Лица	Края	Зеленый	Сим.
триакис тетраэдр "кТ"	усеченный тетраэдр	Равнобедренный Версия 3.6.6			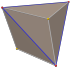112.885 33.557 33.557	129.521	1.0607	12	18	8	Т д
ромбический додекаэдр "Джей Си"	кубооктаэдр	Ромб Версия 3.4.3.4		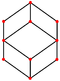	70.529 109.471 70.529 109.471	120	0.8660	12	24	14	Ой ​
триакис октаэдр "кО"	усеченный куб	Равнобедренный Версия 3.8.8			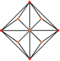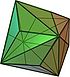117.201 31.400 31.400	147.350	1.7071	24	36	14	Ой ​
тетракис шестигранник "кС"	усеченный октаэдр	Равнобедренный Версия 4.6.6			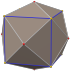83.621 48.190 48.190	143.130	1.5000	24	36	14	Ой ​
дельтовидный икоситетраэдр "оС"	ромбокубооктаэдр	Видеть Версия 3.4.4.4			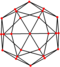81.579 81.579 81.579 115.263	138.118	1.3066	24	48	26	Ой ​
Додекаэдр Дисдякиса "мС"	усеченный кубооктаэдр	Неравносторонний Версия 4.6.8			87.202 55.025 37.773	155.082	2.2630	48	72	26	Ой ​
пятиугольный икоситетраэдр "ГК"	курносый куб	Пентагон В3.3.3.3.4			114.812 114.812 114.812 114.812 80.752	136.309	1.2472	24	60	38	О
ромбический триаконтаэдр "ДжД"	икосододекаэдр	Ромб В3.5.3.5			63.435 116.565 63.435 116.565	144	1.5388	30	60	32	I h
триакис икосаэдр "кИ"	усеченный додекаэдр	Равнобедренный В3.10.10			119.039 30.480 30.480	160.613	2.9271	60	90	32	I h
пентакис додекаэдр "кД"	усеченный икосаэдр	Равнобедренный Версия 5.6.6			68.619 55.691 55.691	156.719	2.4271	60	90	32	I h
дельтовидный шестиконтаэдр "ОД"	ромбикосидодекаэдр	Видеть Версия 3.4.5.4			86.974 67.783 86.974 118.269	154.121	2.1763	60	120	62	I h
триаконтаэдр дисдиакиса "мД"	усеченный икосододекаэдр	Неравносторонний Версия 4.6.10			88.992 58.238 32.770	164.888	3.7694	120	180	62	I h
пятиугольный шестиконтаэдр "гД"	курносый додекаэдр	Пентагон В3.3.3.3.5			118.137 118.137 118.137 118.137 67.454	153.179	2.0971	60	150	92	я

показывать заказано по размеру
The Catalan solids' Archimedean duals, all shown with the same edge length. Sorted by midradius in descending order: All faces of Catalan solids, same scale as above:

Симметрия

Каталонские тела, наряду с их двойственными архимедовыми телами , можно сгруппировать в тела с тетраэдрической, октаэдрической и икосаэдрической симметрией. Как для октаэдрической, так и для икосаэдрической симметрии существует шесть форм. Единственное каталонское тело с подлинной тетраэдрической симметрией — это тетраэдр триакиса (двойник усеченного тетраэдра ). Ромбдодекаэдр . и тетракисгексаэдр обладают октаэдрической симметрией, но их можно раскрасить так, чтобы они имели только тетраэдрическую симметрию Ректификация и курносость также существуют при тетраэдрической симметрии, но они являются платоническими, а не архимедовыми, поэтому их двойниками являются платонические, а не каталонские. (В таблице ниже они показаны на коричневом фоне.)

Тетраэдрическая симметрия

Архимед (Платонический)
каталанский (Платонический)

Октаэдрическая симметрия

Архимед
каталанский

Икосаэдрическая симметрия

Архимед
каталанский

Геометрия

Все двугранные углы каталонского тела равны. Обозначая их значение через $\theta$ , и обозначая угол грани в вершинах, где $p$ лица встречаются $\alpha _{p}$, у нас есть

$\sin(\theta /2)=\cos(\pi /p)/\cos(\alpha _{p}/2)$.

Это можно использовать для вычисления $\theta$ и $\alpha _{p}$, $\alpha _{q}$, ... , от $p$, $q$ ... только.

Треугольные лица

Из 13 каталонских тел 7 имеют треугольные грани. Они имеют вид Vp.qr, где p, q и r принимают значения между 3, 4, 5, 6, 8 и 10. Углы $\alpha _{p}$, $\alpha _{q}$ и $\alpha _{r}$можно вычислить следующим образом. Помещать $a=4\cos ^{2}(\pi /p)$, $b=4\cos ^{2}(\pi /q)$, $c=4\cos ^{2}(\pi /r)$ и положи

$S=-a^{2}-b^{2}-c^{2}+2ab+2bc+2ca$.

Затем

$\cos(\alpha _{p})={\frac {S}{2bc}}-1$,

$\sin(\alpha _{p}/2)={\frac {-a+b+c}{2{\sqrt {bc}}}}$.

Для $\alpha _{q}$ и $\alpha _{r}$выражения, конечно, похожи. Двугранный угол $\theta$ можно вычислить из

$\cos(\theta )=1-2abc/S$.

Применяя это, например, к триаконтаэдру Дисдиакиса ( $p=4$, $q=6$ и $r=10$, следовательно $a=2$, $b=3$ и $c=\phi +2$, где $\phi$ это золотое сечение ) дает $\cos(\alpha _{4})={\frac {2-\phi }{6(2+\phi )}}={\frac {7-4\phi }{30}}$ и $\cos(\theta )={\frac {-10-7\phi }{14+5\phi }}={\frac {-48\phi -155}{241}}$.

Четырехугольные грани

Из 13 каталонских тел 4 имеют четырехугольные грани. Они имеют вид Vp.qpr, где p, q и r принимают значения между 3, 4 и 5. Угол $\alpha _{p}$можно рассчитать по следующей формуле:

$\cos(\alpha _{p})={\frac {2\cos ^{2}(\pi /p)-\cos ^{2}(\pi /q)-\cos ^{2}(\pi /r)}{2\cos ^{2}(\pi /p)+2\cos(\pi /q)\cos(\pi /r)}}$.

Из этого, $\alpha _{q}$, $\alpha _{r}$и двугранный угол можно легко вычислить. Альтернативно, поставьте $a=4\cos ^{2}(\pi /p)$, $b=4\cos ^{2}(\pi /q)$, $c=4\cos ^{2}(\pi /p)+4\cos(\pi /q)\cos(\pi /r)$. Затем $\alpha _{p}$ и $\alpha _{q}$можно найти, применив формулы для треугольного случая. Угол $\alpha _{r}$конечно, можно вычислить аналогичным образом. Лица - коршуны , или, если $q=r$, ромб . Применяя это, например, к дельтовидному икоситетраэдру ( $p=4$, $q=3$ и $r=4$), мы получаем $\cos(\alpha _{4})={\frac {1}{2}}-{\frac {1}{4}}{\sqrt {2}}$.

Пятиугольные грани

Из 13 каталонских тел 2 имеют пятиугольные грани. Они имеют вид Vp.pppq, где p=3 и q=4 или 5. Угол $\alpha _{p}$можно вычислить, решив уравнение третьей степени:

$8\cos ^{2}(\pi /p)\cos ^{3}(\alpha _{p})-8\cos ^{2}(\pi /p)\cos ^{2}(\alpha _{p})+\cos ^{2}(\pi /q)=0$.

Свойства метрики

Для каталонского твердого тела ${\bf {C}}$ позволять ${\bf {A}}$ быть двойственным по отношению к средней сфере ${\bf {C}}$. Затем ${\bf {A}}$представляет собой архимедово тело с такой же средней сферой. Обозначим длину ребер ${\bf {A}}$ к $l$. Позволять $r$ быть радиусом граней ${\bf {C}}$, $r_{m}$ средний радиус ${\bf {C}}$ и ${\bf {A}}$, $r_{i}$ радиус ${\bf {C}}$, и $r_{c}$ радиус окружности ${\bf {A}}$. Тогда эти величины можно выразить через $l$ и двугранный угол $\theta$ следующее:

$r^{2}={\frac {l^{2}}{8}}(1-\cos \theta )$,

$r_{m}^{2}={\frac {l^{2}}{4}}{\frac {1-\cos \theta }{1+\cos \theta }}$,

$r_{i}^{2}={\frac {l^{2}}{8}}{\frac {(1-\cos \theta )^{2}}{1+\cos \theta }}$,

$r_{c}^{2}={\frac {l^{2}}{2}}{\frac {1}{1+\cos \theta }}$.

Эти величины связаны соотношением $r_{m}^{2}=r_{i}^{2}+r^{2}$, $r_{c}^{2}=r_{m}^{2}+l^{2}/4$ и $r_{i}r_{c}=r_{m}^{2}$.

В качестве примера позвольте ${\bf {A}}$ быть кубооктаэдром с длиной ребра $l=1$. Затем ${\bf {C}}$представляет собой ромбдодекаэдр. Применяя формулу для четырехугольных граней с $p=4$ и $q=r=3$ дает $\cos \theta =-1/2$, следовательно $r_{i}=3/4$, $r_{m}={\frac {1}{2}}{\sqrt {3}}$, $r_{c}=1$, $r={\frac {1}{4}}{\sqrt {3}}$.

Все вершины ${\bf {C}}$ типа $p$ лежат на сфере радиуса $r_{c,p}$ данный

$r_{c,p}^{2}=r_{i}^{2}+{\frac {2r^{2}}{1-\cos \alpha _{p}}}$,

и аналогично для $q,r,\ldots$.

Двойственно, существует сфера, которая касается всех граней ${\bf {A}}$ которые являются регулярными $p$-гонов (и аналогично для $q,r,\ldots$) в их центре. Радиус $r_{i,p}$ этой сферы определяется

$r_{i,p}^{2}=r_{m}^{2}-{\frac {l^{2}}{4}}\cot ^{2}(\pi /p)$.

Эти два радиуса связаны соотношением $r_{i,p}r_{c,p}=r_{m}^{2}$. Продолжая приведенный выше пример: $\cos \alpha _{3}=-1/3$ и $\cos \alpha _{4}=1/3$, который дает $r_{c,3}={\frac {3}{8}}{\sqrt {6}}$, $r_{c,4}={\frac {3}{4}}{\sqrt {2}}$, $r_{i,3}={\frac {1}{3}}{\sqrt {6}}$ и $r_{i,4}={\frac {1}{2}}{\sqrt {2}}$.

Если $P$ является вершиной ${\bf {C}}$ типа $p$, $e$ край ${\bf {C}}$ начинается с $P$, и $P^{\prime }$ точка, где находится край $e$ касается средней сферы ${\bf {C}}$, обозначим расстояние $PP^{\prime }$ к $l_{p}$. Затем края ${\bf {C}}$ соединение вершин типа $p$ и введите $q$ иметь длину $l_{p,q}=l_{p}+l_{q}$. Эти величины можно вычислить по формуле

$l_{p}={\frac {l}{2}}{\frac {\cos(\pi /p)}{\sin(\alpha _{p}/2)}}$,

и аналогично для $q,r,\ldots$. Продолжая приведенный выше пример: $\sin(\alpha _{3}/2)={\frac {1}{3}}{\sqrt {6}}$, $\sin(\alpha _{4}/2)={\frac {1}{3}}{\sqrt {3}}$, $l_{3}={\frac {1}{8}}{\sqrt {6}}$, $l_{4}={\frac {1}{4}}{\sqrt {6}}$, поэтому ребра ромбододекаэдра имеют длину $l_{3,4}={\frac {3}{8}}{\sqrt {6}}$.

Двугранные углы $\alpha _{p,q}$между $p$-угольный и $q$-угольные грани ${\bf {A}}$ удовлетворить

$\cos \alpha _{p,q}={\frac {l^{2}}{4}}{\frac {\cot(\pi /p)\cot(\pi /q)}{r_{m}^{2}}}-{\frac {r_{i,p}r_{i,q}}{r_{m}^{2}}}={\frac {l_{p}l_{q}-r_{m}^{2}}{r_{c,p}r_{c,q}}}$.

Завершая пример ромбододекаэдра, двугранный угол $\alpha _{3,4}$ кубооктаэдра определяется выражением $\cos \alpha _{3,4}=-{\frac {1}{3}}{\sqrt {3}}$.

Строительство

Грань любого каталонского многогранника можно получить из вершинной фигуры двойственного архимедова тела с помощью конструкции Дормана-Люка .

Применение к другим твердым телам

Все формулы этого раздела также применимы к Платоновым телам , а также к бипирамидам и трапециям с равными двугранными углами, поскольку их можно вывести только из свойства постоянного двугранного угла. Для пятиугольного трапецоэдра , например, с гранями V3.3.5.3 получим $\cos(\alpha _{3})={\frac {1}{4}}-{\frac {1}{4}}{\sqrt {5}}$, или $\alpha _{3}=108^{\circ }$. В этом нет ничего удивительного: можно срезать обе вершины так, чтобы получить правильный додекаэдр .

См. также

• Список однородных мозаик. Показывает двойные однородные многоугольные мозаики, похожие на каталонские тела.
• Обозначение многогранника Конвея. Процесс построения обозначений.
• Архимедово тело
• Джонсон твердый

Ссылки

• Мемуары Эжена Каталана по теории многогранников. J. l'École Polytechnique (Париж) 41, 1-71, 1865.
• Канди, Х. Мартин ; Роллетт, AP (1961), Математические модели (2-е изд.), Оксфорд: Clarendon Press, MR   0124167 .
• Гайлюнас, П.; Шарп, Дж. (2005), «Двойственность многогранников», Международный журнал математического образования в области науки и технологий , 36 (6): 617–642, doi : 10.1080/00207390500064049 , S2CID   120818796 .
• Алан Холден Формы, пространство и симметрия . Нью-Йорк: Дувр, 1991.
• Веннингер, Магнус (1983), Двойные модели , Издательство Кембриджского университета , ISBN  978-0-521-54325-5 , МР   0730208 (Тринадцать полуправильных выпуклых многогранников и двойственные им)
• Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN  0-486-23729-Х . (Раздел 3-9)
• Энтони Пью (1976). Многогранники: визуальный подход . Калифорния: Издательство Калифорнийского университета в Беркли. ISBN  0-520-03056-7 . Глава 4: Двойники архимедовых многогранников, призмы и антипризмы

Внешние ссылки

• Вайсштейн, Эрик В. «Каталонские твердые тела» . Математический мир .
• Вайсштейн, Эрик В. «Изоэдр» . Математический мир .
• Каталонские тела - в Visual Polyhedra
• Архимедовы двойники – в Многогранниках виртуальной реальности
• Интерактивный каталанский Solid на Java
• Ссылка для скачивания оригинальной каталонской публикации 1865 года с красивыми рисунками, формат PDF