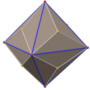
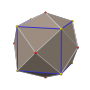
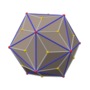
Додекаэдр Пентакиса

Додекаэдр Пентакиса
(Нажмите здесь, чтобы увидеть вращающуюся модель)
Тип	Каталонский солид
Диаграмма Кокстера
Обозначение Конвея	кД
Тип лица	Версия 5.6.6 равнобедренный треугольник
Лица	60
Края	90
Вершины	32
Вершины по типу	20{6}+12{5}
Группа симметрии	I _h , H ₃ , [5,3], (*532)
Группа ротации	Я, [5,3] ⁺, (532)
Двугранный угол	156°43′07″ арккос(- 80 + 9√5 / 109 )
Характеристики	выпуклый, гране-переходный
Усеченный икосаэдр ( двойной многогранник )	Сеть

В геометрии пентакисдодекаэдр пятиугольной или кисдодекаэдр — это многогранник, созданный путем присоединения пирамиды к каждой грани правильного додекаэдра ; то есть это Клитопа додекаэдра. В частности, этот термин обычно относится к определенному каталонскому телу , а именно двойственному к усеченному икосаэдру .

Декартовы координаты [ править ]

Позволять $\phi$ быть золотым сечением . 12 баллов, поставленных $(0,\pm 1,\pm \phi )$ а циклические перестановки этих координат являются вершинами правильного икосаэдра . Его двойственный правильный додекаэдр , ребра которого пересекают ребра икосаэдра под прямым углом, имеет вершинами точки $(\pm 1,\pm 1,\pm 1)$ вместе с точками $(\pm \phi ,\pm 1/\phi ,0)$ и циклические перестановки этих координат. Умножив все координаты икосаэдра на коэффициент $(3\phi +12)/19\approx 0.887\,057\,998\,22$ дает икосаэдр немного меньшего размера. 12 вершин этого икосаэдра вместе с вершинами додекаэдра являются вершинами пентакисдодекаэдра с центром в начале координат. Длина его длинных ребер равна $2/\phi$ . Его грани представляют собой острые равнобедренные треугольники с одним углом $\arccos((-8+9\phi )/18)\approx 68.618\,720\,931\,19^{\circ }$ и двое из $\arccos((5-\phi )/6)\approx 55.690\,639\,534\,41^{\circ }$ . Отношение длин длинной и короткой сторон этих треугольников равно $(5-\phi )/3\approx 1.127\,322\,003\,75$ .

Химия [ править ]

Пентакис -додекаэдр в модели бакминстерфуллерена : каждый (сферический) сегмент поверхности представляет собой углерода атом , и если все заменить плоскими гранями, образуется пентакис-додекаэдр. Аналогично, усеченный икосаэдр представляет собой модель бакминстерфуллерена, каждая вершина которого представляет собой атом углерода.

Биология [ править ]

Пентакис -додекаэдр также является моделью некоторых икосаэдрически-симметричных вирусов, таких как аденоассоциированный вирус . Они содержат 60 капсидных белков, связанных с симметрией, которые в совокупности образуют 60 симметричных граней пентакисдодекаэдра .

Ортогональные проекции [ править ]

Додекаэдр пентакиса имеет три положения симметрии: два в вершинах и одно в среднем ребре:

Ортогональные проекции
Проективный симметрия	[2]	[6]	[10]
Изображение
Двойной изображение

Вогнутый додекаэдр - пентакис

Вогнутый пентакисдодекаэдр заменяет пятиугольные грани додекаэдра перевернутыми пирамидами.

Выпуклый (слева) и вогнутый (справа) пентакисдодекаэдр

Связанные многогранники [ править ]

Грани правильного додекаэдра можно заменить (или дополнить) любой правильной пятиугольной пирамидой, чтобы получить так называемый приподнятый додекаэдр . Например, если использовать пятиугольные пирамиды с равносторонними треугольниками, в результате получится невыпуклый дельтаэдр . Любой такой приподнятый додекаэдр имеет ту же комбинаторную структуру, что и пентакисдодекаэдр, т. е. ту же диаграмму Шлегеля .

Семейство однородных икосаэдрических многогранников.
Symmetry: [5,3], (*532)							[5,3]⁺, (532)


{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Duals to uniform polyhedra

V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

* n 32 мутация симметрии усеченных мозаик: n .6.6 v т и
Sym. *n42 [n,3]	Spherical				Euclid.	Compact		Parac.	Noncompact hyperbolic
Sym. *n42 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Truncated figures
Config.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	∞.6.6	12i.6.6	9i.6.6	6i.6.6
n-kis figures
Config.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V∞.6.6	V12i.6.6	V9i.6.6	V6i.6.6

См. также [ править ]

Раскопанный додекаэдр

ссылки Культурные

Структура космического корабля «Земля» в Уолта Диснея Мира Эпкоте является производной додекаэдра пентакиса.
Модель студенческой художественной мастерской, спроектированная Джеффри Линдси, на самом деле представляла собой полусферический пентакис-додекаэдр https://books.google.com/books?id=JD8EAAAAMBAJ&dq=jeffrey+lindsay&pg=PA92
Форма «Хрустального купола», использованного в популярном телеигре « Хрустальный лабиринт», была основана на додекаэдре пентакиса.
В «Докторе Атомике» форма первой атомной бомбы, взорванной в Нью-Мексико, представляла собой пентакис-додекаэдр. [1]
В De Blob 2 в Prison Zoo купола состоят из частей додекаэдра Пентакиса. Эти купола также появляются всякий раз, когда игрок трансформируется в куполе на уровне Hypno Ray.
Некоторые геокупола, на которых играют люди, — это пентакис додекаэдры или, по крайней мере, приподнятые додекаэдры.

Ссылки [ править ]

Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN 0-486-23729-Х . (Раздел 3-9)
Селларс, Питер (2005). «Доктор Атомик Либретто» . Бузи и Хоукс. Мы окружаем плутониевое ядро из тридцати двух точек, равномерно расположенных вокруг его поверхности, тридцать две точки — это центры двадцати треугольных граней икосаэдра, переплетенных с двенадцатью пятиугольными гранями додекаэдра.
Веннингер, Магнус (1983). Двойные модели . Издательство Кембриджского университета . ISBN 978-0-521-54325-5 . МР 0730208 . (Тринадцать полуправильных выпуклых многогранников и их двойственные, стр. 18, Пентакисдодекаэдр)
Симметрии вещей 2008, Джон Х. Конвей, Хайди Бургель, Хаим Гудман-Штраус, ISBN 978-1-56881-220-5 [2] (Глава 21, Названия архимедовых и каталонских многогранников и мозаик, страница 284, додекаэдр Пентакиса)

Внешние ссылки [ править ]

Вайсштейн, Эрик В. , « Додекаэдр Пентакиса » (« каталонское тело ») в MathWorld .
Пентакис Додекаэдр – Интерактивная модель многогранника
Визуальные многогранники пентакис додекаэдр