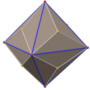
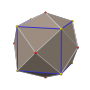
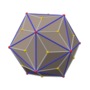
Ромбический додекаэдр

Ромбический додекаэдр
(Нажмите здесь, чтобы увидеть вращающуюся модель)
Тип	Каталонский солид
Диаграмма Кокстера
Обозначение Конвея	ДжейСи
Тип лица	Версия 3.4.3.4 ромб
Лица	12
Края	24
Вершины	14
Вершины по типу	8{3}+6{4}
Группа симметрии	О h , B 3 , [4,3], (*432)
Группа ротации	О, [4,3] + , (432)
Двугранный угол	120°
Характеристики	выпуклый, грани-переходный изоэдр , изотоксал , параллелоэдр
Кубооктаэдр ( двойной многогранник )	Сеть

3D модель ромбододекаэдра

В геометрии ромбдодекаэдр конгруэнтными — выпуклый многогранник с . ромбическими гранями 12 Он имеет 24 ребра и 14 вершин 2-х типов. Это каталонское тело и многогранник кубооктаэдру . двойственный

Свойства

Ромбический додекаэдр является зоноэдром . Его двойственным многогранником является кубооктаэдр . Длина длинной диагонали лица ровно в √ 2 раза больше длины короткой диагонали лица; таким образом, острые углы на каждой грани равны arccos( 1/3 ° . ), или примерно 70,53

Будучи двойственным архимедовому многограннику , ромбический додекаэдр является транзитивным по граням , что означает, что группа симметрии твердого тела действует транзитивно на его наборе граней. Проще говоря, это означает, что для любых двух граней A и B происходит вращение или отражение твердого тела, в результате чего оно занимает одну и ту же область пространства при перемещении грани A к грани B.

Ромбический додекаэдр можно рассматривать как выпуклую оболочку объединения вершин куба и октаэдра. 6 вершин, где встречаются 4 ромба, соответствуют вершинам октаэдра , а 8 вершин, где встречаются 3 ромба, соответствуют вершинам куба .

Ромбический додекаэдр — один из девяти выпуклых многогранников с переходными ребрами , остальные — пять Платоновых тел , кубооктаэдр , икосододекаэдр и ромбический триаконтаэдр .

Ромбический додекаэдр можно использовать для мозаики трехмерного пространства: его можно складывать друг на друга, чтобы заполнить пространство, так же, как шестиугольники заполняют плоскость.

Этот многогранник в мозаике, заполняющей пространство, можно рассматривать как мозаику Вороного гранецентрированной кубической решетки . Это зона Бриллюэна объемноцентрированных кубических (ОЦК) кристаллов. Некоторые минералы, такие как гранат, образуют ромбо-додекаэдрические кристаллы . Как отметил Иоганн Кеплер в своей книге о снежинках ( Strena seu de Nive Sexangula ) 1611 года, медоносные пчелы используют геометрию ромбических додекаэдров для формирования сот из мозаики ячеек, каждая из которых представляет собой шестиугольную призму, увенчанную половиной ромбического додекаэдра. Ромбдодекаэдр появляется также в элементарных ячейках алмаза и алмазоидов . В этих случаях четыре вершины (чередующиеся тройные) отсутствуют, но химические связи лежат на остальных ребрах.

График ромбического додекаэдра негомильтонов .

Ромбический додекаэдр можно разрезать на 4 тупоугольных тригональных трапецоэдра вокруг его центра. Эти ромбоэдры представляют собой ячейки тригонально-трапецоэдрических сот . Аналогия: правильный шестиугольник можно разрезать на 3 ромба вокруг его центра. Эти ромбы представляют собой плитки ромба .

В коллекции Лувра имеется штамп в форме ромбододекаэдра, датируемый птолемеевским Египтом . На лицах написаны греческие буквы, представляющие цифры от 1 до 12: Α Β Γ Δ Ε Ϛ Z Η Θ Ι ΙΑ ΙB. Функция штампа неизвестна.

• 
  Ромбододекаэдр, рассеченный на 4 ромбоэдра.
• 
  Шестиугольник, разрезанный на 3 ромба
• 
  Кристалл граната ​
• 
  Эта анимация показывает построение ромбододекаэдра из куба путем инвертирования пирамид с центральной гранью куба.

Размеры

Обозначая длину ребра ромбододекаэдра,

• радиус к каждой из вписанной сферы ( касательной граней ромбододекаэдра) равен

$r_{\mathrm {i} }={\frac {\sqrt {6}}{3}}~a\approx 0.816\,496\,5809~a\quad$ ( ОЭИС : A157697 ),

• радиус его средней сферы равен

$r_{\mathrm {m} }={\frac {2{\sqrt {2}}}{3}}~a\approx 0.942\,809\,041\,58~a\quad$ ( ОЭИС : A179587 ),

• радиус сферы, проходящей через шесть вершин порядка 4, но не через восемь вершин порядка 3, равен

$r_{\mathrm {o} }={\frac {2{\sqrt {3}}}{3}}~a\approx 1.154\,700\,538~a\quad$ ( ОЭИС : A020832 ),

• радиус сферы, проходящей через восемь вершин порядка 3, в точности равен длине сторон

$r_{\mathrm {t} }=a$

Площадь и объём

Площадь поверхности A и объем V ромбододекаэдра с длиной ребра a равны:

$A=8{\sqrt {2}}~a^{2}\approx 11.313\,7085~a^{2}$

$V={\frac {16{\sqrt {3}}}{9}}~a^{3}\approx 3.079\,201\,44~a^{3}$

Ортогональные проекции

Ромбический додекаэдр имеет четыре специальные ортогональные проекции вдоль осей симметрии с центрами на грани, ребре и двух типах вершин: тройном и четверном. Последние два соответствуют _{B 2} и A ₂ плоскостям Кокстера .

Ортогональные проекции

Проективный симметрия	[4]	[6]	[2]	[2]
ромбический додекаэдр
Кубооктаэдр (двойной)

Декартовы координаты

Вариации пиритоэдра между кубом и ромбдодекаэдром

Расширение ромбододекаэдра

Для длины ребра √3 восемь вершин, где три грани встречаются под тупыми углами, имеют декартовы координаты :

(±1, ±1, ±1)

Координаты шести вершин, где четыре грани встречаются под острыми углами:

(±2, 0, 0), (0, ±2, 0) и (0, 0, ±2)

Ромбический додекаэдр можно рассматривать как вырожденный предельный случай пиритоэдра с перестановкой координат (±1, ±1, ±1) и (0, 1 + h , 1 − h ² ) с параметром h = 1.

Эти координаты иллюстрируют, что ромбдодекаэдр можно рассматривать как куб с квадратной пирамидой, прикрепленной к каждой грани, и что шесть квадратных пирамид могут сложиться вместе в куб того же размера, т. е. ромбдодекаэдр имеет вдвое больший объем, чем вписанный. куб с ребрами, равными коротким диагоналям ромба.

формы

Топологический ромбдодекаэдр можно увидеть внутри шестиугольной призмы с шестиугольниками, разделенными на ромбы дополнительными способами между верхом и низом.

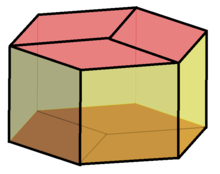
Параллелоэдр

Ромбический додекаэдр — это параллелоэдр , заполняющий пространство многогранник , додекаэдр , двойственный тетраоктаэдрилу или полукубическим сотам и описываемый двумя диаграммами Кокстера : и . Благодаря симметрии D _3d его можно рассматривать как вытянутый тригональный трапецоэдр .

Ромбический додекаэдр , может мозаику пространства посредством трансляционных копий самого себя , как и звездчатый ромбический додекаэдр .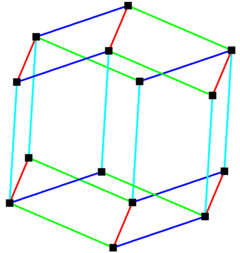

Ромбический додекаэдр можно построить с 4 наборами по 6 параллельных ребер.

Двугранный ромбдодекаэдр

Другие конструкции симметрии ромбододекаэдра также являются заполняющими пространство и как параллелоэдры подобны вариациям заполняющих пространство усеченных октаэдров .

Например, с 4 квадратными гранями и ромбическими гранями под углом 60 градусов и _{D 4h} двугранной симметрией порядка 16. Его можно рассматривать как кубооктаэдр с квадратными пирамидами, увеличенными сверху и снизу.

Сеть

Координаты (0, 0, ±2) (±1, ±1, 0) (±1, 0, ±1) (0, ±1, ±1)

Травяной додекаэдр

Основная статья: додекаэдр Билинского

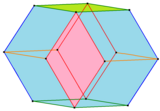Додекаэдр Билинского, ребра и передние грани которого окрашены в соответствии с положением их симметрии.

Додекаэдр Билинского, раскрашенный параллельными гранями.

В 1960 году Станко Билински открыл второй ромбический додекаэдр с 12 конгруэнтными ромбическими гранями — додекаэдр Билинского . Он имеет ту же топологию, но другую геометрию. Ромбические грани в этой форме имеют золотое сечение .

Лица

Первая форма	Вторая форма
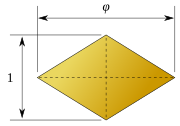√ 2 :1	√ 5 + 1 / 2 :1

Дельтоидный додекаэдр

Рисунок и кристаллическая модель дельтовидного додекаэдра.

Другая топологически эквивалентная вариация, иногда называемая дельтовидным додекаэдром , является изоэдрическим с тетраэдрическим порядком симметрии 24, искажающим ромбические грани в змеи (дельтоиды). Он имеет 8 вершин, скорректированных внутрь или наружу в чередующихся наборах по 4, причем предельный случай представляет собой тетраэдрическую оболочку. Вариации могут быть параметризованы с помощью ( a , b ), где b и a зависят друг от друга, так что тетраэдр, определяемый четырьмя вершинами грани, имеет нулевой объем, т.е. является плоской гранью. (1,1) — ромбическое решение. По приближения мере 1/2 b , . бесконечности приближается к Это всегда так 1 / а + 1 / b = 2, при a , b > 1 / 2 .

(±2, 0, 0), (0, ±2, 0), (0, 0, ±2)

( а , а , а ), (- а , - а , а ), (- а , а , - а ), ( а , - а , - а )

(- б , - б , - б ), (- б , б , б ), ( б , - б , б ), ( б , б , - б )

(1,1)	( 7 / 8 , 7 / 6 )	( 3 / 4 , 3 / 2 )	( 2 / 3 ,2)	( 5 / 8 , 5 / 2 )	( 9 / 16 , 9 / 2 )

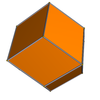Связанные многогранники

Сферический ромбдодекаэдр

showОднородные октаэдрические многогранники
Symmetry: [4,3], (*432)							[4,3]+ (432)	[1+,4,3] = [3,3] (*332)		[3+,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{31,1}	t{3,4} t{31,1}	{3,4} {31,1}	rr{4,3} s2{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	s{3,4} s{31,1}
		=	=	=				= or	= or	=
Duals to uniform polyhedra
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

При проецировании на сферу (см. справа) можно увидеть, что ребра составляют ребра двух тетраэдров, расположенных в своих двойных положениях (стелла-октангула). Эта тенденция продолжается с дельтоидным икоситетраэдром и дельтоидным гексеконтаэдром для двойственных пар других правильных многогранников (наряду с треугольной бипирамидой, если учитывать неправильные мозаики), что дает этой форме альтернативное систематическое название дельтоидного додекаэдра .

* n 32 мутация симметрии двойных расширенных мозаик: V3.4. № .4

Симметрия * № 32 [н,3]	сферический				Евклид.	Компактный гиперб.		Парако.
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Фигура Конфиг.	Версия 3.4.2.4	Версия 3.4.3.4	Версия 3.4.4.4	Версия 3.4.5.4	Версия 3.4.6.4	Версия 3.4.7.4	Версия 3.4.8.4	V3.4.∞.4

Этот многогранник является частью последовательности ромбических многогранников и мозаик с [ n ,3] симметрией группы Кокстера . Куб можно рассматривать как ромбический шестигранник, где ромбы — это квадраты.

showМутации симметрии двойственных квазирегулярных мозаик: V(3.n) 2
*n32	Spherical			Euclidean	Hyperbolic
	*332	*432	*532	*632	*732	*832...	*∞32
Tiling
Conf.	V(3.3)2	V(3.4)2	V(3.5)2	V(3.6)2	V(3.7)2	V(3.8)2	V(3.∞)2

show* n 42 мутации симметрии квазирегулярных двойственных мозаик: V (4.n) 2
Symmetry *4n2 [n,4]	Spherical	Euclidean	Compact hyperbolic				Paracompact	Noncompact
	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]	[iπ/λ,4]
Tiling   Conf.	V4.3.4.3	V4.4.4.4	V4.5.4.5	V4.6.4.6	V4.7.4.7	V4.8.4.8	V4.∞.4.∞	V4.∞.4.∞

Аналогично это относится и к бесконечной серии мозаик с конфигурациями граней V3.2 n .3.2 n , первая из которых находится в евклидовой плоскости, а остальные - в гиперболической плоскости.

Версия 3.4.3.4 (Нарисовано в виде сети )

Версия 3.6.3.6 Замощение евклидовой плоскости Ромбическая плитка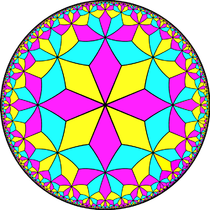

В3.8.3.8 Гиперболическая плоская мозаика (Нарисовано в модели диска Пуанкаре )

Звездочки

Как и многие выпуклые многогранники, ромбдодекаэдр можно построить звездчато , расширяя грани или ребра до тех пор, пока они не встретятся, образуя новый многогранник. Несколько таких созвездий описал Дорман Люк.

На этой анимации показано построение звездчатого ромбододекаэдра путем переворачивания пирамид центральной грани ромбододекаэдра.

Первая звездчатая форма, которую часто называют просто звездчатым ромбдодекаэдром , хорошо известна. Его можно рассматривать как ромбдодекаэдр, каждая грань которого увеличена за счет присоединения к нему пирамиды с ромбическим основанием, с такой высотой пирамиды, что стороны лежат в плоскостях граней соседних граней:

• 
  Первая звездчатая форма ромбододекаэдра.
• 
  3D-модель разложения на 12 пирамид и 4 полукуба

Лука описывает еще четыре звездчатости: вторую и третью (расширяющиеся наружу), одна образовалась путем удаления второй из третьей, а другая путем добавления исходного ромбического додекаэдра обратно к предыдущему.

Второй	Третий
Большой звездчатый ромбдодекаэдр	Звездчатый ромбдодекаэдр

Связанные многогранники

В идеальной проекции «сначала вершина» две вершины тессеракта (отмечены бледно-зеленым цветом) проецируются точно в центр ромбододекаэдра.

Ромбический додекаэдр образует оболочку проекции тессеракта с вершины в три измерения. Существует ровно два способа разложения ромбдодекаэдра на четыре конгруэнтных ромбоэдра , что дает восемь возможных ромбоэдров как проекции 8 кубических ячеек тессеракта. Одним набором проективных векторов являются: u = (1,1,−1,−1), v = (−1,1,−1,1), w = (1,−1,−1,1).

Ромбический додекаэдр образует максимальное поперечное сечение 24-клеточного , а также образует оболочку его параллельной проекции с первой вершины в три измерения. Ромбический додекаэдр можно разложить на шесть конгруэнтных (но неправильных) квадратных дипирамид, встречающихся в одной вершине в центре; они образуют изображения шести пар октаэдрических ячеек 24-клеток. Остальные 12 октаэдрических ячеек выступают на грани ромбододекаэдра. Неравномерность этих изображений обусловлена ​​проективными искажениями; грани 24-клеточного числа представляют собой правильные октаэдры в 4-мерном пространстве.

Это разложение дает интересный метод построения ромбододекаэдра: разрежьте куб на шесть равных квадратных пирамид и прикрепите их к граням второго куба. Треугольные грани каждой пары соседних пирамид лежат в одной плоскости и поэтому сливаются в ромбы. Аналогичным образом можно построить 24-ячейку с использованием двух тессерактов .

и культурный

Эксперт по архитектуре Джеймс Д. Венн определил, что философские значения и значения, закодированные в зданиях, связаны со значениями, связанными с ромбическим додекаэдром такими мыслителями, как Платон .

К зданиям, в которых используется такой код, относятся:

• Соултон Холл ,
• Колледж Гонвилл и Кайус, Кембридж
• Дом Верулама , ныне утраченный дом Фрэнсиса Бэкона.
• Воллатон Холл

Практическое использование

В реактивных колес компоновке тетраэдрическая космического корабля обычно используется конфигурация из четырех колес. Для колес, которые работают одинаково (с точки зрения пикового крутящего момента и максимального углового момента) в обоих направлениях вращения и для всех четырех колес, максимальный крутящий момент и максимальный импульс для 3-осевой системы ориентации (с учетом идеализированных приводов) определяются путем проецирования тессеракт , представляющий пределы крутящего момента или импульса каждого колеса в трехмерном пространстве через матрицу осей колес 3 × 4; полученный трехмерный многогранник представляет собой ромбдодекаэдр. Такое расположение реактивных колес не является единственно возможной конфигурацией (более простая конструкция состоит из трех колес, установленных с возможностью вращения вокруг ортогональных осей), но она выгодна тем, что обеспечивает резервирование для смягчения отказа одного из четырех колес (с ухудшением общих характеристик). доступно из оставшихся трех активных колес) и обеспечивает более выпуклую оболочку, чем куб, что приводит к меньшей зависимости маневренности от направления оси (с точки зрения привода/установки). Массовые свойства космического корабля влияют на общий импульс и маневренность системы, поэтому уменьшение отклонения границ оболочки не обязательно приводит к увеличению однородности смещений предпочтительных осей (то есть даже при идеально распределенном пределе производительности внутри подсистемы привода предпочтительные оси вращения не обязательно являются произвольными). на уровне системы).

Многогранник также является основой сетки HEALPix , используемой в космологии для хранения и управления картами космического микроволнового фона , а также в компьютерной графике для хранения карт окружающей среды .

См. также

• Додекаэдр
• Ромбический триаконтаэдр
• Трапезо-ромбический додекаэдр
• Усеченный ромбдодекаэдр
• 24-клеточный – 4D аналог ромбододекаэдра
• Строительные системы Архимед
• Полностью усеченный ромбдодекаэдр

Дальнейшее чтение

• Уильямс, Роберт (1979), Геометрическая основа естественной структуры: справочник по дизайну , Dover Publications, Inc, ISBN  0-486-23729-Х (Раздел 3-9)
• Веннингер, Магнус (1983), Двойные модели , Издательство Кембриджского университета, номер документа : 10.1017/CBO9780511569371 , ISBN  978-0-521-54325-5 , MR   0730208 (Тринадцать полуправильных выпуклых многогранников и двойственные им многогранники, стр. 19, Ромбический додекаэдр)
• Симметрии вещей 2008, Джон Х. Конвей, Хайди Бургель, Хаим Гудман-Штраус, ISBN   978-1-56881-220-5 (Глава 21, Названия архимедовых и каталонских многогранников и мозаик, стр. 285, Ромбический додекаэдр)

Внешние ссылки

• Вайсштейн, Эрик В. , «Ромбдодекаэдр» , MathWorld
• Многогранники виртуальной реальности – Энциклопедия многогранников

Компьютерные модели

• Связь ромбического триаконтаэдра и ромбического додекаэдра , 5-соединения ромбического додекаэдра и 5-соединения ромбического додекаэдра, автор: Шандор Кабаи, Демонстрационный проект Вольфрама .

Бумажные проекты

• Календарь из ромбдодекаэдра – сделать календарь из ромбдодекаэдра без клея.
• Еще один календарь из ромбических додекаэдров , сделанный путем плетения бумажных полосок.

Практическое применение

• Институт Архимеда Примеры реальных проектов жилищного строительства с использованием этой геометрии