Усеченный икосаэдр
| Усеченный икосаэдр | |
|---|---|
 (Нажмите здесь, чтобы увидеть вращающуюся модель) | |
| Тип | Архимедово тело Однородный многогранник |
| Элементы | F = 32, E = 90, V = 60 (χ = 2) |
| Лица по сторонам | 12{5}+20{6} |
| Обозначение Конвея | из |
| Символы Шлефли | т{3,5} |
| т 0,1 {3,5} | |
| Символ Витхоффа | 2 5 | 3 |
| Диаграмма Кокстера | |
| Группа симметрии | I h , H 3 , [5,3], (*532), порядок 120 |
| Группа ротации | Я , [5,3] + , (532), порядок 60 |
| Двугранный угол | 6-6: 138.189685° 6-5: 142.62° |
| Ссылки | У 25 , С 27 , Ж 9 |
| Характеристики | Полуправильный выпуклый |
 Цветные лица |  5.6.6 ( фигура вершины ) |
 Додекаэдр Пентакиса ( двойной многогранник ) | 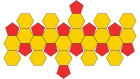 Сеть |
В геометрии икосаэдр усеченный представляют — архимедово тело , одно из 13 выпуклых изогональных непризматических тел, 32 грани которых собой два или более типов правильных многоугольников . Это единственная из этих фигур, которая не содержит треугольников и квадратов. В общем случае предполагается, что степень усечения одинакова, если не указано иное.
Он имеет 12 правильных пятиугольных граней, 20 правильных шестиугольных граней, 60 вершин и 90 ребер.
Это многогранник Гольдберга GP V (1,1) или {5+,3} 1,1 , содержащий пятиугольные и шестиугольные грани.
Эта геометрия связана с футбольными мячами, обычно украшенными белыми шестиугольниками и черными пятиугольниками; Adidas Telstar был первым футбольным мячом, в котором использовался этот рисунок в 1970-х годах. Геодезические купола, подобные тем, чью архитектуру впервые разработал Бакминстер Фуллер, часто основаны на этой структуре. Это также соответствует геометрии молекулы фуллерена C 60 («бакибол»).
Он используется в транзитивной по ячейкам гиперболической мозаике, заполняющей пространство, в усеченных додекаэдрических сотах пятого порядка .
Строительство [ править ]

Этот многогранник можно построить из икосаэдра путем усечения или обрезки каждой из 12 вершин на отметке одной трети каждого ребра, создавая 12 пятиугольных граней и преобразуя исходные 20 треугольных граней в правильные шестиугольники. [1] [2]
Характеристики [ править ]
В геометрии и теории графов существуют некоторые стандартные характеристики многогранников .
Декартовы координаты [ править ]
Декартовы координаты вершин усеченного икосаэдра с центром в начале координат являются четными перестановками :
где это золотая середина . Радиус описанной окружности а ребра имеют длину 2. [3]
Ортогональные проекции [ править ]
имеет Усеченный икосаэдр пять особых ортогональных проекций , центрированных по вершине, по двум типам ребер и двум типам граней: шестиугольной и пятиугольной. Последние два соответствуют A 2 и H 2 плоскостям Кокстера .
| В центре | Вертекс | Край 5-6 | Край 6-6 | Лицо Шестиугольник | Лицо Пентагон |
|---|---|---|---|---|---|
| Твердый |  |  |  | ||
| Каркас |  | 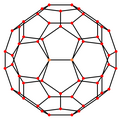 |  |  |  |
| Проективный симметрия | [2] | [2] | [2] | [6] | [10] |
| Двойной | 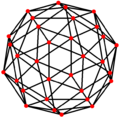 | 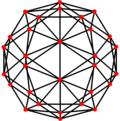 |  |  |  |
Сферическая черепица [ править ]
Усеченный икосаэдр также можно представить в виде сферической мозаики и спроецировать на плоскость с помощью стереографической проекции . Эта проекция является равноугольной , сохраняющей углы, но не площади или длины. Прямые линии на сфере проецируются на плоскость в виде дуг окружностей.
 |  пятиугольник в центре |  шестиугольник с центром |
| Ортографическая проекция | Стереографические проекции | |
|---|---|---|
Размеры [ править ]
Если длина ребра усеченного икосаэдра равна a , радиус ( описанной сферы той, которая касается усеченного икосаэдра во всех вершинах) равен:
где φ — золотое сечение .
Этот результат легко получить, используя в качестве отправной точки для наших рассуждений один из трёх ортогональных золотых прямоугольников, нарисованных в исходном икосаэдре (до отсечения). Угол между отрезками, соединяющими центр и вершинами, соединенными общим краем (рассчитанный на основе этой конструкции), равен примерно 23,281446°.
Площадь и объём [ править ]
Площадь A и объем V усеченного икосаэдра с длиной ребра a [4] являются:
Приложения [ править ]
Мячи, используемые в футбольном и командном гандболе, являются, пожалуй, самым известным примером сферического многогранника, аналога усеченного икосаэдра, встречающегося в повседневной жизни. [5] Мяч состоит из тех же правильных пятиугольников и правильных шестиугольников, но имеет более сферическую форму из-за давления воздуха внутри и эластичности мяча. Этот тип мяча был представлен на чемпионате мира в 1970 году (начиная с 2006 года этот культовый дизайн был заменен альтернативными моделями ).
Геодезические купола обычно основаны на треугольных гранях этой геометрии с примерами структур, найденных по всему миру и популяризированных Бакминстером Фуллером . [6]
Такая же форма была также конфигурацией линз, используемых для фокусировки взрывных ударных волн детонаторов как в гаджете, так и «Толстяк» в атомных бомбах . [7]
Усеченный икосаэдр можно также описать как модель молекулы бакминстерфуллерена (фуллерена) (С 60 ), или «бакибола», – аллотропа элементарного углерода, открытого в 1985 году. Диаметр футбольного мяча и молекулы фуллерена составляют 22 см. и около 0,71 нм соответственно, следовательно, соотношение размеров составляет ≈31 000 000:1.
В популярной ремесленной культуре большие блестящие шары можно сделать с использованием рисунка икосаэдра и пластиковых, пенопластовых или бумажных стаканчиков.
В искусстве [ править ]
- Галерея
- Усеченный икосаэдр (слева) в сравнении с футбольным мячом .
- фуллерена C 60 Молекула
- Усеченный обтекатель метеостанции икосаэдрический
- Усеченный икосаэдр, выточенный из алюминия 6061-T6.
- Деревянный усеченный икосаэдр работы Джорджа Харта .
Связанные многогранники [ править ]
| Семейство однородных икосаэдрических многогранников. |
|---|
| * n 32 мутация симметрии усеченных мозаик: n .6.6 |
|---|
Эти однородные звездчатые многогранники и одна икосаэдрическая звездчатка имеют неоднородные усеченные икосаэдры, выпуклые оболочки :
| Однородные звездчатые многогранники с усеченными икосаэдрами и выпуклыми оболочками. |
|---|
Этот многогранник похож на однородный додекаэдр со скошенными краями , который имеет 12 пятиугольников и 30 шестиугольников.
Усеченный граф икосаэдра [ править ]
| Усеченный икосаэдрический граф | |
|---|---|
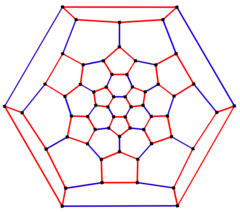 шестикратной симметрии Диаграмма Шлегеля | |
| Вершины | 60 |
| Края | 90 |
| Автоморфизмы | 120 |
| Хроматическое число | 3 |
| Характеристики | Кубический , гамильтонов , регулярный , нуль-симметричный |
| Таблица графиков и параметров | |
В математической области теории графов усеченный икосаэдрический граф — это граф вершин и ребер усеченного икосаэдра , одного из архимедовых тел . Он имеет 60 вершин и 90 ребер и является кубическим архимедовым графом . [8] [9] [10]
 5-кратная симметрия | 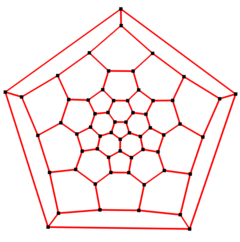 5-кратная диаграмма Шлегеля |
История [ править ]

Усеченный икосаэдр был известен Архимеду , который классифицировал 13 архимедовых тел в утерянном труде. Все, что мы знаем о его работе над этими формами, исходит от Паппа Александрийского , который просто перечисляет количество граней каждой: 12 пятиугольников и 20 шестиугольников, в случае усеченного икосаэдра. Первое известное изображение и полное описание усеченного икосаэдра взято из повторного открытия Пьеро делла Франчески в его книге XV века De quinque corporibus Regularibus . [11] который включал пять архимедовых тел (пять усечений правильных многогранников). Ту же форму изобразил Леонардо да Винчи в своих иллюстрациях к плагиату Луки Пачоли книги делла Франчески в 1509 году. Хотя Альбрехт Дюрер исключил эту форму из других архимедовых тел, перечисленных в его книге 1525 года о многогранниках Underweysung der Messung , его описание было найдено в его посмертных статьях, опубликованных в 1538 году. Позже Иоганн Кеплер заново открыл полный список 13 архимедовых тел, включая усечённый икосаэдр, и включил их в свою книгу 1609 года «Harmonices Mundi» . [12]
См. также [ править ]
- Фуллеры
- Бакминстерфуллерен (С 60 )
- Гиперболический футбольный мяч
- Равновеликая проекция Снайдера
- Футбольный мяч
Примечания [ править ]
- ^ Медников Евгений Георгиевич; Джуэлл, Мэтью С.; Даль, Лоуренс Ф. (1 сентября 2007 г.). «Наноразмерный (μ 12 -Pt)Pd 164- x Pt x (CO) 72 (PPh 3 ) 20 ( x ≈ 7), содержащий Pt-центрированное четырехоболочное ядро из 165 атомов Pd-Pt с беспрецедентными межоболочечными мостиковыми карбонильными лигандами: сравнительный Анализ моделей роста икосаэдрической оболочки с геометрически связанным Pd 145 (CO) x (PEt 3 ) 30 (x ≈ 60), содержащим трехоболочное ядро Pd 145 с колпачком» . Журнал Американского химического общества . 129 (37): 11624. doi : 10.1021/ja073945q . ISSN 0002-7863 . ПМИД 17722929 .
- ^ Кочик, Дитер (июль – август 2006 г.). «Топология и комбинаторика футбольных мячей» . Американский учёный . 94 (4): 350. дои : 10.1511/2006.60.350 .
- ^ Вайсштейн, Эрик В. «Группа икосаэдра» . Математический мир .
- ^ Вайсштейн, Эрик В. «Усеченный икосаэдр» . mathworld.wolfram.com . Проверено 10 сентября 2023 г.
- ^ Кочик, Дитер (2006). «Топология и комбинаторика футбольных мячей». Американский учёный . 94 (4): 350–357. дои : 10.1511/2006.60.350 .
- ^ Кребс, Альбин (2 июля 1983 г.). «Р. Бакминстер Фуллер мертв; футуристы построили геодезический купол» . Нью-Йорк Таймс . Нью-Йорк, штат Нью-Йорк, с. 1 . Проверено 7 ноября 2021 г.
- ^ Роудс, Ричард (1996). Тёмное солнце: создание водородной бомбы . Книги пробного камня. стр. 195 . ISBN 0-684-82414-0 .
- ^ Читай, RC; Уилсон, Р.Дж. (1998). Атлас графов . Издательство Оксфордского университета . п. 268.
- ^ Годсил, К. и Ройл, Г. Алгебраическая теория графов Нью-Йорк: Springer-Verlag, стр. 211, 2001 г.
- ^ Костант, Б. График усеченного икосаэдра и последнее письмо Галуа. Замечания амер. Математика. Соц. 42, 1995, стр. 959-968 PDF.
- ^ Кац, Юджин А. (2011). «Мосты между математикой, естественными науками, архитектурой и искусством: случай фуллеренов». Искусство, наука и технологии: взаимодействие трех культур: материалы первой международной конференции . стр. 60–71.
- ^ Филд, СП (1997). «Заново открывая архимедовы многогранники: Пьеро делла Франческа, Лука Пачоли, Леонардо да Винчи, Альбрехт Дюрер, Даниэле Барбаро и Иоганн Кеплер». Архив истории точных наук . 50 (3–4): 241–289. дои : 10.1007/BF00374595 . JSTOR 41134110 . МР 1457069 . S2CID 118516740 .
Ссылки [ править ]
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN 0-486-23729-Х . (Раздел 3-9)
- Кромвель, П. (1997). «Архимедовы тела». Многогранники: «Одна из самых очаровательных глав геометрии» . Кембридж: Издательство Кембриджского университета. стр. 79–86. ISBN 0-521-55432-2 . OCLC 180091468 .
Внешние ссылки [ править ]
- Вайсштейн, Эрик В. , « Усеченный икосаэдр » (« Архимедово тело ») в MathWorld .
- Клитцинг, Ричард. «3D выпуклые однородные многогранники x3x5o - ti» .
- Редактируемая для печати сетка усеченного икосаэдра с интерактивным 3D-просмотром
- Однородные многогранники
- «Многогранники виртуальной реальности» — Энциклопедия многогранников
- 3D-визуализация бумажных данных Мяч чемпионата мира по футболу
![{\displaystyle {\begin{aligned}{5}{\Bigl(}&&0,&&\pm\,1,&&\pm\,3\varphi {\Bigr)},\\[2pt]{\Bigl(} &&\pm \,1,&&\quad \pm \,(2+\light ),&&\pm \,2\light {\Bigr )},\\[2pt]{\Bigl (}&&\pm \, \varphi ,&&\pm \,2,&&\quad \pm \,(2\varphi +1){\Bigr )},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23246fa2e710bc39e22b4b5438ea081efe7e2c0b)