Пирамида (геометрия)

Из Википедии, бесплатной энциклопедии

В геометрии пирамида πυραμίς ( древнегреческого пурамис ( ) ) от [1] [2] представляет собой многогранник , образованный соединением многоугольного основания и точки, называемой вершиной . Каждое базовое ребро и вершина образуют треугольник, называемый боковой гранью . Это коническое тело с многоугольным основанием. Многие типы пирамид можно найти, определив форму оснований или отрезав вершину. Ее можно обобщить до более высокого измерения, известного как гиперпирамида . Все пирамиды самодвойственны .

Определение [ править ]

Части пирамиды

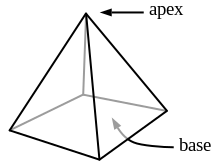
Пирамида — это многогранник, который может быть образован соединением многоугольного основания и точки, называемой вершиной . Каждый ребро основания и вершина образуют равнобедренный треугольник, называемый боковой гранью . [3] Ребра, соединяющие вершины многоугольного основания с вершиной, называются боковыми ребрами . [4] Исторически определение пирамиды было описано многими математиками еще в древности. Евклид в своих «Началах» определял пирамиду как твердую фигуру, построенную из одной плоскости в одну точку. Контекст его определения был расплывчатым, пока Герон Александрийский не определил его как фигуру, соединив точку с многоугольным основанием. [5]

Призматоид , определяется как многогранник, вершины которого лежат в двух параллельных плоскостях, а боковые грани представляют собой треугольники трапеции и параллелограммы . [6] Пирамиды относят к призматоидным. [7]

Классификация и виды [ править ]

Семейство правильных многоугольных пирамид с основанием: тетраэдр, квадратная пирамида, пятиугольная пирамида и шестиугольная пирамида.

Правильная пирамида — это пирамида, основание которой описано вокруг круга, а высота пирамиды совпадает в центре круга. [8] Эту пирамиду можно классифицировать по регулярности ее оснований. Пирамида, имеющая в основании правильный многоугольник, называется правильной пирамидой . [9] Пирамида с n - сторонним правильным основанием имеет n + 1 вершину, n + 1 грань и 2 n ребер. [10] Такая пирамида имеет равнобедренные треугольники в качестве граней, а ее симметрия 2 C n v , симметрия порядка n : пирамиды симметричны, поскольку они вращаются вокруг своей оси симметрии (линии, проходящей через вершину и центр тяжести основания), и они зеркально симметричны относительно любой перпендикулярной плоскости, проходящей через биссектрису основания. [11] [12] Примерами являются квадратная пирамида и пятиугольная пирамида , четырех- и пятитреугольная пирамида с квадратным и пятиугольным основанием соответственно; они классифицируются как первое и второе тело Джонсона, если их правильные грани и ребра равны по длине, а их симметрия равна C 4v порядка 8 и C 5v порядка 10 соответственно. Тетраэдр или треугольная пирамида — это пример четырех равносторонних треугольников, все ребра которых равны по длине, и один из них считается основанием. Поскольку грани правильные , это пример платоновского тела и дельтаэдров , а также тетраэдрическая симметрия . [13] [14] Пирамида с основанием в виде круга называется конусом . [15] Пирамиды обладают свойством самодвойственности , то есть их двойственные вершины совпадают с вершинами, соответствующими ребрам, и наоборот. [16] Их скелет можно представить в виде графа-колеса . [17]

Пирамиды с прямоугольными и ромбическими основаниями.

Правильная пирамида также может иметь в основании неправильный многоугольник. Примерами являются пирамиды с прямоугольником и ромбом в основании. Эти две пирамиды имеют симметрию C 2v четвертого порядка.

Пирамида, усеченная наклонной плоскостью
Пирамида в основании пентаграммы .

Тип пирамид можно вывести разными способами. Регулярность основания пирамиды может быть классифицирована в зависимости от типа многоугольника, и одним из примеров является пирамида с правильным звездчатым многоугольником в качестве основания, известная как звездная пирамида . [18] Пирамида, отрезанная плоскостью, называется усеченной пирамидой ; если плоскость усечения параллельна основанию пирамиды, ее называют усеченной пирамидой .

Измерение [ править ]

Площадь поверхности — это общая площадь граней каждого многогранника. В случае пирамиды площадь ее поверхности равна сумме площадей треугольников и площади многоугольного основания.

Объем пирамиды равен произведению одной трети площади основания на высоту. При условии это площадь базы и это высота пирамиды. Математически объем пирамиды равен: [19]

Объем пирамиды был зафиксирован еще в Древнем Египте, где вычислили объем усеченного квадрата , предполагая, что они познакомились с объемом квадратной пирамиды. [20] Формула объема общей пирамиды была открыта индийским математиком Арьябхатой , где он процитировал в своей «Арьябхатии» , что объем пирамиды неверно равен полупродукту площади основания и высоты. [21]

Обобщение [ править ]

Основная статья: Гиперпирамида
4-мерная гиперпирамида с кубом в основании

Гиперпирамида — это обобщение пирамиды в n - мерном пространстве. В случае пирамиды все вершины основания, многоугольника на плоскости, соединяются с точкой вне плоскости, которая является вершиной . Высота пирамиды – это расстояние вершины от плоскости. Эта конструкция обобщается на n измерений. База становится ( n − 1) -многогранником в ( n − 1) -мерной гиперплоскости. Точка, называемая вершиной, расположена вне гиперплоскости и соединяется со всеми вершинами многогранника, а расстояние вершины от гиперплоскости называется высотой. [22]

n n - мерный объем - мерной гиперпирамиды можно вычислить следующим образом:

Здесь V n обозначает n - мерный объем гиперпирамиды. A обозначает ( n − 1) - мерный объем основания, а h - высоту, то есть расстояние между вершиной и ( n - 1) - содержащей основание A. мерной гиперплоскостью , [22]

Ссылки [ править ]

  1. ^ «Генри Джордж Лидделл, Роберт Скотт, Греко-английский лексикон, πυραμίς» , www.perseus.tufts.edu .
  2. ^ Это слово означало «своего рода лепешку из жареных зерен пшеницы, консервированных в меду»; египетские пирамиды были названы в честь своей формы. Видеть Бикс, Роберт С. (2009), Этимологический словарь греческого языка , Брилл, стр. 1261 .
  3. ^ Кромвель, Питер Р. (1997), Многогранники , издательство Кембриджского университета, стр. 13 .
  4. ^ Смит, Джеймс Т. (2000), Методы геометрии , John Wiley & Sons, стр. 98, ISBN  0-471-25183-6 .
  5. ^ Хит, Томас (1908), Евклид: Тринадцать книг элементов , том. 3, Издательство Кембриджского университета, с. 268 .
  6. ^ Альсина, Клауди; Нельсен, Роджер Б. (2015), Математическая космическая одиссея: твердотельная геометрия в 21 веке , Математическая ассоциация Америки , стр. 85 .
  7. ^ Грюнбаум, Бранко (1997), «Изогональные призматоиды», Дискретная и вычислительная геометрия , 18 : 13–52, doi : 10.1007/PL00009307 .
  8. ^ Поля, Г. (1954), Математика и правдоподобные рассуждения: индукция и аналогия в математике , Princeton University Press, стр. 138 .
  9. ^ О'Лири, Майкл (2010), Революции геометрии , John Wiley & Sons, стр. 10 .
  10. ^ Хамбл, Стив (2016), «Математика для экспериментатора: математические занятия с компьютерной поддержкой» , Тейлор и Фрэнсис, стр. 23 .
  11. ^ Джонсон, Норман В. (2018), Геометрия и преобразования , ISBN  978-1-107-10340-5 . См. главу 11: Группы конечной симметрии, 11.3 Пирамиды, призмы и антипризмы.
  12. ^ Александрофф, Пол (2012), Введение в теорию групп , Dover Publications, стр. 48, ISBN  978-0-486-48813-4 .
  13. ^ Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Canadian Journal of Mathematics , 18 : 169–200, doi : 10.4153/cjm-1966-021-8 , MR   0185507 , S2CID   122006114 , Zbl   0132.14603 . См. таблицу III, строка 1.
  14. ^ Уэхара, Рюхей (2020), Введение в вычислительное оригами: мир новой вычислительной геометрии , Springer, стр. 62, номер домена : 10.1007/978-981-15-4470-5 , ISBN  978-981-15-4470-5 .
  15. ^ Келли, В. Майкл (2009), Огромная книга задач по геометрии , Penguin Group, стр. 455 .
  16. ^ Воллебен, Ева (2019), «Дуальность в неполиэдрических телах, часть I: Полилайнер», в Коккьярелле, Луиджи (редактор), ICGG 2018 - Материалы 18-й Международной конференции по геометрии и графике: 40-летие - Милан, Италия, 3-7 августа 2018 г. , Спрингер, с. 485–486, номер домена : 10.1007/978-3-319-95588-9 , ISBN.  978-3-319-95588-9
  17. ^ Писанский, Томаж; Серватиус, Бриджит (2013), Конфигурация с графической точки зрения , Springer, стр. 21, номер домена : 10.1007/978-0-8176-8364-1 , ISBN  978-0-8176-8363-4 .
  18. ^ Веннингер, Магнус Дж. (1974), Модели многогранников , издательство Кембриджского университета, стр. 50, ISBN  978-0-521-09859-5 , заархивировано из оригинала 11 декабря 2013 г.
  19. ^ Александр, Дэниел С.; Кеберлин, Джералин М. (2014), Элементарная геометрия для студентов колледжей (6-е изд.), Cengage Learning, стр. 403, ISBN  978-1-285-19569-8 .
  20. ^ Гиллингс, Р.Дж. (1964), «Объем усеченной пирамиды в древнеегипетских папирусах», Учитель математики , 57 (8): 552–555, JSTOR   27957144 .
  21. ^ Каджори, Флориан (1991), История математики (5-е изд.), Американское математическое общество, стр. 87, ISBN  978-1-4704-7059-3 .
  22. ^ Перейти обратно: а б Матай, А.М. (1999), Введение в геометрическую вероятность: аспекты распределения с приложениями , Тейлор и Фрэнсис, с. 42–43 .

См. также [ править ]

Внешние ссылки [ править ]

Викискладе есть медиафайлы, связанные с пирамидами (геометрией) .
Retrieved from "https://en.wikipedia.org/w/index.php?title=Pyramid_(geometry)&oldid=1203179470"