Дельтаэдр


В геометрии дельтаэдр дельтаэдры ( множественное число ) — это многогранник которого грани , все представляют собой ( конгруэнтные ) равносторонние треугольники . Название взято от греческой заглавной буквы дельта (Δ), имеющей форму равностороннего треугольника. Дельтаэдров бесконечно много. По лемме о рукопожатии каждый дельтаэдр имеет четное количество граней. Только восемь дельтаэдров строго выпуклые ; у них 4, 6, 8, 10, 12, 14, 16 и 20 граней. [1] Эти восемь дельтаэдров с соответствующим количеством граней, ребер и вершин перечислены ниже.
Восемь строго выпуклых дельтаэдров
[ редактировать ]дельтаэдров восемь Строго выпуклых : три — правильные многогранники и Платоновы тела , пять — тела Джонсона .
| Изображение | Имя | Лица | Края | Вершины | Конфигурации вершин | Группа симметрии |
|---|---|---|---|---|---|---|
 | Тетраэдр | 4 | 6 | 4 | 4 × 3 3 | Т д , [3,3] |
 | Октаэдр | 8 | 12 | 6 | 6 × 3 4 | Ох ] , [4,3 |
 | Икосаэдр | 20 | 30 | 12 | 12 × 3 5 | I h , [5,3] |
| Изображение | Имя | Лица | Края | Вершины | Конфигурации вершин | Группа симметрии |
|---|---|---|---|---|---|---|
 | Треугольная бипирамида | 6 | 9 | 5 | 2 × 3 3 3 × 3 4 | Д 3ч , [3,2] |
 | Пятиугольная бипирамида | 10 | 15 | 7 | 5 × 3 4 2 × 3 5 | Д 5ч , [5,2] |
 | Курносый дисфеноид | 12 | 18 | 8 | 4 × 3 4 4 × 3 5 | Д 2д , [4,2 + ] |
 | Триаугментированная треугольная призма | 14 | 21 | 9 | 3 × 3 4 6 × 3 5 | Д 3ч , [3,2] |
 | Гироудлиненная квадратная бипирамида | 16 | 24 | 10 | 2 × 3 4 8 × 3 5 | Д 4д , [8,2 + ] |
В 6-гранном дельтаэдре некоторые вершины имеют степень 3, а некоторые - 4. В 10-, 12-, 14- и 16-гранных дельтаэдрах некоторые вершины имеют степень 4, а некоторые - степень 5. Эти пять неправильных дельтаэдров относятся к классу тел Джонсона : неоднородных строго выпуклых многогранников с правильными многоугольниками в качестве граней.
Дельтаэдр сохраняет свою форму: даже если его края могут свободно вращаться вокруг своих вершин (так что углы между ними плавные), они не перемещаются. Не все многогранники обладают этим свойством: например, если некоторые углы куба ослабить , он может деформироваться в непрямоугольную призму или даже в ромбоэдр без прямого угла вообще .
18-гранного строго выпуклого дельтаэдра не существует. [2] Однако икосаэдр со суженными краями дает пример октадекаэдра , который можно либо сделать строго выпуклым с 18 неправильными треугольными гранями, либо сделать равносторонним с 18 (правильными) треугольными гранями, которые включают два набора по три копланарных треугольника.
Нестрого выпуклые случаи
[ редактировать ]Существует бесконечно много случаев с копланарными треугольниками, допускающими выпуклые сечения бесконечной треугольной мозаики . Если наборы копланарных треугольников считать одной гранью, можно посчитать меньший набор граней, ребер и вершин. Компланарные треугольные грани можно объединить в ромбические, трапециевидные, шестиугольные или другие многоугольные грани. Каждая грань должна представлять собой выпуклый многогранник , например ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , ... [3]
, ... [3]
Вот некоторые небольшие примеры:
| Изображение | Имя | Лица | Края | Вершины | Конфигурации вершин | Группа симметрии |
|---|---|---|---|---|---|---|
 | Дополненный октаэдр Увеличение 1 тет + 1 окт. | 10 | 15 | 7 | 1 × 3 3 3 × 3 4 3 × 3 5 0 × 3 6 | С 3в , [3] |
| 4 3 | 12 | |||||
 | Трехугольный трапецоэдр Увеличение 2 тета + 1 окт. | 12 | 18 | 8 | 2 × 3 3 0 × 3 4 6 × 3 5 0 × 3 6 | Д 3д , [6,2 + ] |
| 6 | 12 | |||||
 | Увеличение 2 тета + 1 окт. | 12 | 18 | 8 | 2 × 3 3 1 × 3 4 4 × 3 5 1 × 3 6 | С 2в , [2] |
| 2 2 2 | 11 | 7 | ||||
 | Треугольная деталь Увеличение 3 тета + 1 окт. | 14 | 21 | 9 | 3 × 3 3 0 × 3 4 3 × 3 5 3 × 3 6 | С 3в , [3] |
| 1 3 1 | 9 | 6 | ||||
 | Вытянутый октаэдр Увеличение 2 тета + 2 октавы | 16 | 24 | 10 | 0 × 3 3 4 × 3 4 4 × 3 5 2 × 3 6 | Д 2ч , [2,2] |
| 4 4 | 12 | 6 | ||||
 | Тетраэдр Увеличение 4 тета + 1 окт. | 16 | 24 | 10 | 4 × 3 3 0 × 3 4 0 × 3 5 6 × 3 6 | Т д , [3,3] |
| 4 | 6 | 4 | ||||
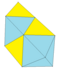 | Увеличение 3 тета + 2 октавы | 18 | 27 | 11 | 1 × 3 3 2 × 3 4 5 × 3 5 3 × 3 6 | {Идентификатор,R} где R — отражение через плоскость |
| 2 1 2 2 | 14 | 9 | ||||
 | Икосаэдр со суженным ребром | 18 | 27 | 11 | 0 × 3 3 2 × 3 4 8 × 3 5 1 × 3 6 | С 2в , [2] |
| 12 2 | 22 | 10 | ||||
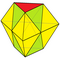 | Треугольный бифрустум Увеличение 6 тетов + 2 октавы | 20 | 30 | 12 | 0 × 3 3 3 × 3 4 6 × 3 5 3 × 3 6 | Д 3ч , [3,2] |
| 2 6 | 15 | 9 | ||||
 | Треугольный купол Увеличение 4 тета + 3 октавы | 22 | 33 | 13 | 0 × 3 3 3 × 3 4 6 × 3 5 4 × 3 6 | С 3в , [3] |
| 3 3 1 1 | 15 | 9 | ||||
 | Треугольная бипирамида Увеличение 8 тетов + 2 октавы | 24 | 36 | 14 | 2 × 3 3 3 × 3 4 0 × 3 5 9 × 3 6 | Д 3ч , [3,2] |
| 6 | 9 | 5 | ||||
 | Шестиугольная антипризма | 24 | 36 | 14 | 0 × 3 3 0 × 3 4 12 × 3 5 2 × 3 6 | Д 6д , [12,2 + ] |
| 12 2 | 24 | 12 | ||||
 | Усеченный тетраэдр Увеличение 6 тетов + 4 октавы | 28 | 42 | 16 | 0 × 3 3 0 × 3 4 12 × 3 5 4 × 3 6 | Т д , [3,3] |
| 4 4 | 18 | 12 | ||||
 | Тетракис кубооктаэдр Октаэдр Увеличение 8 тетов + 6 окт. | 32 | 48 | 18 | 0 × 3 3 12 × 3 4 0 × 3 5 6 × 3 6 | Ох ] , [4,3 |
| 8 | 12 | 6 |
Невыпуклые формы
[ редактировать ]Существует бесконечное количество невыпуклых дельтаэдров.
Пять невыпуклых дельтаэдров можно получить, добавив равностороннюю пирамиду к каждой грани платонова тела :
Равносторонние платоновые тела, дополненные пирамидой Изображение 

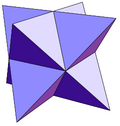


Имя Тетраэдр Триакиса Тетракис шестигранник Октаэдр Триакиса
( Стелла восьмиугольная )Додекаэдр Пентакиса Триакис икосаэдр Лица 12 
24 
60 
Другие невыпуклые дельтаэдры можно получить путем сборки нескольких правильных тетраэдров :
Как и все тороидальные многогранники , тороидальные дельтаэдры невыпуклые; пример:
Когда это возможно, добавление перевернутой равносторонней пирамиды к каждой грани многогранника дает невыпуклый дельтаэдр; пример:
Как и все самопересекающиеся многогранники, самопересекающиеся дельтаэдры невыпуклые; пример:
- Большой икосаэдр — тело Кеплера-Пуансо с 20 пересекающимися треугольниками:
См. также
[ редактировать ]- Симплициальный многогранник - многогранник со всеми симплексными гранями.
Ссылки
[ редактировать ]- ^ Фрейденталь, Х ; ван дер Варден, Б.Л. (1947), «Оверинг ван Евклида («Об утверждении Евклида»)», Саймон Стевин (на голландском языке), 25 : 115–128 (Они показали, что существует всего восемь строго выпуклых дельтаэдров. )
- ^ Тригг, Чарльз В. (1978), «Бесконечный класс дельтаэдров», Mathematics Magazine , 51 (1): 55–57, doi : 10.1080/0025570X.1978.11976675 , JSTOR 2689647 .
- ^ Выпуклые дельтаэдры и допуск копланарных граней
Дальнейшее чтение
[ редактировать ]- Раузенбергер О. (1915), «Выпуклые псевдоправильные многогранники», Журнал математического и научного образования , 46 : 135–142 .
- Канди, Х. Мартин (декабрь 1952 г.), «Дельтаэдры», Mathematical Gazette , 36 : 263–266, doi : 10.2307/3608204 , JSTOR 3608204 .
- Канди, Х. Мартин ; Роллетт, А. (1989), «3.11. Дельтаэдры», Математические модели (3-е изд.), Стрэдброк, Англия: Tarquin Pub., стр. 142–144 .
- Гарднер, Мартин (1992), Фрактальная музыка, гиперкарты и многое другое: математические развлечения от Scientific American , Нью-Йорк: WH Freeman, стр. 40, 53 и 58–60 .
- Пью, Энтони (1976), Многогранники: визуальный подход , Калифорния: Издательство Калифорнийского университета в Беркли, ISBN. 0-520-03056-7 , стр. 35–36.










