Лемма о рукопожатии

В этом графе четное количество вершин (четыре вершины с номерами 2, 4, 5 и 6) имеют нечетные степени. Сумма степеней всех шести вершин равна 2 + 3 + 2 + 3 + 3 + 1 = 14 , что вдвое больше количества ребер.

В теории графов , разделе математики, лемма о рукопожатии — это утверждение, что в каждом конечном неориентированном графе число вершин, соприкасающихся с нечетным числом ребер, четно. Например, если есть группа людей, которые пожимают друг другу руки, число людей, которые пожимают руки нечетному числу других людей, является четным. ^[1] Лемма о рукопожатии является следствием формулы суммы степеней , также иногда называемой леммой о рукопожатии: ^[2] согласно которому сумма степеней ( количества касаний каждой вершины) равна удвоенному количеству ребер в графе. Оба результата были доказаны Леонардом Эйлером ( 1736 ) в его знаменитой статье о семи мостах Кенигсберга, положившей начало изучению теории графов. ^[3]

Помимо проблемы семи мостов Кенигсберга, которая впоследствии формализовала эйлеровы туры , другие применения формулы суммы степеней включают доказательства определенных комбинаторных структур. Например, при доказательстве леммы Спернера и задачи о восхождении на гору обычно возникают геометрические свойства формулы. Класс сложности PPA инкапсулирует сложность поиска второй нечетной вершины при наличии одной такой вершины в большом неявно определенном графе .

Определения и утверждения [ править ]

Неориентированный граф состоит из системы вершин и ребер , соединяющих неупорядоченные пары вершин. В любом графе степень $\deg(v)$ вершины $v$ определяется как количество ребер, имеющих $v$ как конечная точка. Для графов, которым разрешено содержать петли, соединяющие вершину с самой собой, цикл следует считать вносящим две единицы в степень его конечной точки для целей леммы о согласовании. ^[2] Тогда лемма о рукопожатии утверждает, что в каждом конечном графе должно существовать четное число вершин, для которых $\deg(v)$ является нечетным числом. ^[1] Вершины нечетной степени в графе иногда называют нечетными узлами (или нечетными вершинами ); ^[4] В этой терминологии лемму о согласовании можно перефразировать как утверждение, что каждый граф имеет четное количество нечетных узлов. ^[4]^[5]

Формула суммы степеней гласит, что

\sum _{v\in V}\deg v=2|E|,

где

V

- это набор узлов (или вершин) в графе и

E

— множество ребер графа. То есть сумма степеней вершин равна удвоенному количеству ребер. ^[6] В ориентированных графах другая форма формулы суммы степеней гласит, что сумма входящих степеней всех вершин и сумма исходящих степеней равны количеству ребер. Здесь входная степень — это количество входящих ребер, а исходящая степень — это количество исходящих ребер. ^[7] Версия формулы суммы степеней также применима к конечным семействам множеств или, что то же самое, мультиграфам : сумма степеней элементов (где степень равна количеству содержащих его множеств) всегда равна сумме мощностей множеств. . ^[8]

Оба результата применимы также к любому подграфу данного графа и, в частности, к его связным компонентам . Следствием этого является то, что для любой нечетной вершины должен существовать путь, соединяющий ее с другой нечетной вершиной. ^[9]

Приложения [ править ]

Пути и туры Эйлера [ править ]

Схематический вид семи мостов Кенигсберга.

Граф с вершинами для каждого участка суши и ребром для каждого моста

Леонард Эйлер впервые доказал лемму о рукопожатии в своей работе о семи мостах Кенигсберга , предложив совершить пешеходную экскурсию по городу Кенигсбергу (ныне Калининград ), пересекая каждый из семи его мостов один раз. Это можно перевести в термины теории графов как поиск эйлерова пути или эйлерова обхода связного графа, представляющего город и его мосты: обход графа, который пересекает каждое ребро один раз и заканчивается в вершине, отличной от той, в которой он начинается в в случае эйлерова пути или возвращение к исходной точке в случае эйлерова обхода. Эйлер сформулировал фундаментальные результаты для этой проблемы с точки зрения количества нечетных вершин в графе, которое лемма о установлении связи ограничивает четным числом. Если это число равно нулю, существует эйлеров путь, а если оно равно двум, существует эйлеров путь. В противном случае проблему невозможно решить. В случае «Семи мостов Кенигсберга» граф, представляющий задачу, имеет четыре нечетные вершины и не имеет ни эйлерова пути, ни эйлерова обхода. ^[3] Поэтому было невозможно обойти все семь мостов Кенигсберга, не повторив мост.

В алгоритме Христофидеса–Сердюкова аппроксимации задачи коммивояжера геометрические следствия формулы суммы степеней играют жизненно важную роль, позволяя алгоритму соединять вершины попарно, чтобы построить граф, на котором эйлеров тур образует приближенный тур TSP. . ^[10]

Комбинаторное перечисление [ править ]

Можно показать, что несколько комбинаторных структур четны по количеству, связав их с нечетными вершинами в соответствующем «графе обмена». ^[11]

Например, как доказал К.Э.Б. Смит , в любом кубическом графе $G$ должно пройти четное количество гамильтоновых циклов через любое фиксированное ребро $uv$ ; это циклы, которые проходят через каждую вершину ровно один раз. Томасон (1978) использовал доказательство, основанное на лемме о согласовании, чтобы распространить этот результат на графы, в которых все вершины имеют нечетную степень. Томасон определяет граф обмена $H$ , вершины которого находятся во взаимно однозначном соответствии с гамильтоновыми путями в $G$ начиная с $u$ и продолжаем через край $uv$ . Два таких пути $p_{1}$ и $p_{2}$ определяются как соединенные ребром в $H$ если можно получить $p_{2}$ добавив новое ребро в конец $p_{1}$ и удаляем еще один край из середины $p_{1}$ . Эта операция обратима, образуя симметричное отношение , поэтому $H$ является неориентированным графом. Если путь $p$ заканчивается в вершине $w$ , то вершина, соответствующая $p$ в $H$ имеет степень, равную числу способов, которыми $p$ может быть продлен ребром, который не соединяется обратно с $u$ ; то есть степень этой вершины в $H$ либо $\deg(w)-1$ (четное число), если $p$ не входит в гамильтонов цикл через $uv$ , или $\deg(w)-2$ (нечетное число), если $p$ является частью гамильтонова цикла через $uv$ . С $H$ имеет четное количество нечетных вершин, $G$ должно иметь четное число гамильтоновых циклов через $uv$ . ^[12]

Другие приложения [ править ]

Лемма о рукопожатии (или формула суммы степеней) также используется в доказательстве ряда других результатов в математике. К ним относятся следующие:

Раскраска Спернера треугольного треугольника, затененная, чтобы выделить три маленьких треугольника, которые имеют все три цвета вершин.

Лемма Спернера гласит, что если большой треугольник разделить на меньшие треугольники, соединяющиеся ребром к краю, и вершины помечены тремя цветами так, что вдоль каждого края большого треугольника используются только два цвета, то по крайней мере один треугольников меньшего размера имеет вершины всех трех цветов; он имеет приложения в теоремах о неподвижной точке , алгоритмах поиска корней и справедливом делении . Одним из доказательств этой леммы является граф обмена, вершинами которого являются треугольники (как маленькие, так и большие), а ребра соединяют пары треугольников, которые имеют две общие вершины некоторых двух цветов. В этом графе обмена большой треугольник обязательно имеет нечетную степень, как и маленький треугольник всех трех цветов, но не другие маленькие треугольники. По лемме о рукопожатии должно быть нечетное количество маленьких треугольников всех трех цветов, и, следовательно, должен существовать хотя бы один такой треугольник. ^[13]

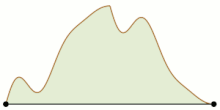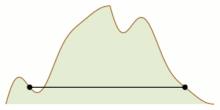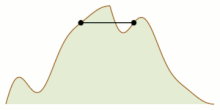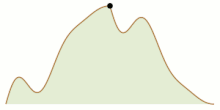
утверждает Задача альпинизма , что для достаточно хорошо ведущих себя функций на единичном интервале с равными значениями на концах интервала можно скоординировать движение двух точек, начиная с противоположных концов интервала, так, что они встречаются где-то посередине, оставаясь в точках равной ценности на протяжении всего движения. Одно из доказательств этого включает в себя аппроксимацию функции кусочно-линейной функцией с одинаковыми крайними точками, параметризацию положения двух движущихся точек координатами одной точки в единичном квадрате и показ того, что доступные положения для двух точек образуют конечный граф, вложенный в этот квадрат, имеющий только начальную позицию и ее обращение в качестве нечетных вершин. По лемме о квитировании эти две позиции принадлежат одной и той же связной компоненте графа, и путь от одной к другой обязательно проходит через искомую точку встречи. ^[14]
Гипотеза реконструкции касается проблемы однозначного определения структуры графа из мультимножества подграфов, образованного удалением из него единственной вершины. Учитывая эту информацию, формулу суммы степеней можно использовать для восстановления количества ребер в данном графе и степеней каждой вершины. Отсюда можно определить, является ли данный граф регулярным графом , и если да, то определить его однозначно из любого подграфа, удаленного по вершинам, путем добавления нового соседа для всех вершин подграфа слишком низкой степени. Следовательно, все регулярные графы можно восстановить. ^[15]
В игре « Гекс» участвуют два игрока, которые размещают фигуры своего цвета на мозаике параллелограмма доски в форме шестиугольниками до тех пор, пока у одного игрока не будет соединенный путь соседних фигур от одной стороны доски к другой. Она никогда не может закончиться вничью: к тому времени, как доска полностью заполнится фигурами, у одного из игроков будет сформирован выигрышный путь. Одним из доказательств этого является граф из заполненного игрового поля с вершинами в углах шестиугольников и ребрами на сторонах шестиугольников, разделяющими цвета двух игроков. Этот граф имеет четыре нечетные вершины в углах доски и четные вершины в других местах, поэтому он должен содержать путь, соединяющий два угла, который обязательно имеет выигрышный путь для одного игрока на одной из своих сторон. ^[16]

Доказательство [ править ]

Доказательство Эйлера формулы суммы степеней использует технику двойного счета : он подсчитывает количество инцидентных пар. $(v,e)$ где $e$ это ребро и вершина $v$ является одной из его конечных точек двумя разными способами. Вертекс $v$ принадлежит $\deg(v)$ пары, где $\deg(v)$ (степень $v$ ) — число инцидентных ему ребер. Следовательно, количество инцидентных пар есть сумма степеней. Однако каждое ребро графа принадлежит ровно двум инцидентным парам, по одному на каждую из его конечных точек; следовательно, число инцидентных пар равно $2|E|$ . Поскольку эти две формулы учитывают один и тот же набор объектов, они должны иметь равные значения. То же доказательство можно интерпретировать как суммирование элементов матрицы инцидентности графа двумя способами: по строкам, чтобы получить сумму степеней, и по столбцам, чтобы получить удвоенное количество ребер. ^[5]

Для графов лемма о согласовании является следствием формулы суммы степеней. ^[8] В сумме целых чисел на четность суммы не влияют четные члены суммы; общая сумма четна, если имеется четное количество нечетных членов, и нечетна, если имеется нечетное количество нечетных членов. Поскольку одна часть формулы суммы степеней представляет собой четное число $2|E|$ , сумма на другой стороне должна иметь четное количество нечетных членов; то есть должно быть четное число вершин нечетной степени. ^[5]

В качестве альтернативы можно использовать математическую индукцию для доказательства формулы суммы степеней: ^[2] или напрямую доказать, что количество вершин нечетной степени четно, удаляя по одному ребру за раз из данного графа и используя анализ случаев степеней его конечных точек, чтобы определить влияние этого удаления на четность числа вершин нечетной степени. ^[17]

В специальных классах графов [ править ]

Граф Клебша , регулярный пятой степени, имеет четное число вершин (16) и число ребер (40), кратное пяти.

Ромбический додекаэдр двуправильный , с шестью вершинами четвертой степени и восемью вершинами третьей степени; 6 × 4 = 8 × 3 = 24 — количество ребер.

Обычные графики [ править ]

Формула суммы степеней подразумевает, что каждый $r$ - обычный график с $n$ вершин имеет $nr/2$ края. ^[18] Поскольку количество ребер должно быть целым числом, отсюда следует, что когда $r$ нечетно, количество вершин должно быть четным. ^[19] Кроме того, для нечетных значений $r$ , количество ребер должно делиться на $r$ . ^[20]

Двудольные и двурегулярные графы [ править ]

В двудольном графе вершины разделены на два подмножества, причем каждое ребро имеет одну конечную точку в каждом подмножестве. Из того же рассуждения о двойном подсчете следует, что в каждом подмножестве сумма степеней равна числу ребер в графе. В частности, оба подмножества имеют равные суммы степеней. ^[21] Для бирегулярных графов с разбиением вершин на подмножества $V_{1}$ и $V_{2}$ с каждой вершиной в подмножестве $V_{i}$ имеющий степень $r_{i}$ , должно быть так, что $|V_{1}|r_{1}=|V_{2}|r_{2}$ ; оба равны количеству ребер. ^[22]

Бесконечные графики [ править ]

Бесконечный граф только с одной нечетной вершиной

Лемма о рукопожатии не применима в своей обычной форме к бесконечным графам, даже если они имеют только конечное число вершин нечетной степени. Например, бесконечный граф путей с одной конечной точкой имеет только одну вершину нечетной степени, а не четное количество таких вершин. Однако можно сформулировать версию леммы о согласовании, используя понятие конца , класса эквивалентности полубесконечных путей («лучей»), рассматривающих два луча как эквивалентные, когда существует третий луч, который использует бесконечно много вершин из каждый из них. Степень конца — это максимальное количество содержащихся в нем лучей, не пересекающихся по краям, и конец является нечетным, если его степень конечна и нечетна. В более общем смысле, можно определить конец как нечетный или четный, независимо от того, имеет ли он бесконечную степень, в графах, все вершины которых имеют конечную степень. Тогда в таких графах число нечетных вершин и нечетных концов, сложенных вместе, либо четное, либо бесконечное. ^[23]

Подграфы [ править ]

По теореме Галлаи вершины любого графа можно разложить как $V=V_{e}\cup V_{o}$ где $G(V_{e})$ имеет все степени четные и $G(V_{o})$ имеет все степени нечетные с $|V_{o}|$ даже по лемме о рукопожатии. В 1994 году Яир Каро ^[24] доказал, что $|V_{o}|/|V|>1/{\sqrt {n}}$ а в 2021 году препринт Фербера Асафа и Михаила Кривелевича показал, что $|V_{o}|/|V|>1/10000$ . ^[25]^[26]

Вычислительная сложность [ править ]

В связи с методом графа обмена для доказательства существования комбинаторных структур представляет интерес вопрос, насколько эффективно можно найти эти структуры. Например, предположим, что в качестве входных данных задан гамильтонов цикл в кубическом графе; из теоремы Смита следует, что существует второй цикл. Как быстро можно найти этот второй цикл? Пападимитриу (1994) исследовал вычислительную сложность подобных вопросов или, в более общем смысле, поиска второй вершины нечетной степени, когда задана единственная нечетная вершина в большом неявно определенном графе . Он определил класс сложности PPA для инкапсуляции таких проблем, как эта; ^[27] тесно связанный класс, определенный на ориентированных графах, PPAD , привлек значительное внимание в алгоритмической теории игр , поскольку вычисление равновесия Нэша вычислительно эквивалентно самым сложным задачам этого класса. ^[28]

Вычислительные задачи, которые оказались полными для класса сложности PPA, включают вычислительные задачи, связанные с леммой Спернера. ^[29] и к справедливому разделению ресурсов согласно теореме Хобби-Райса . ^[30]

Примечания [ править ]

^ Jump up to: Перейти обратно: ^а ^б Хейн, Джеймс Л. (2015), «Пример 3: Проблема установления связи» , Дискретные структуры, логика и вычислимость , Jones & Bartlett Publishers, стр. 703, ISBN 9781284070408
^ Jump up to: Перейти обратно: ^а ^б ^с Гундерсон, Дэвид С. (2014), Справочник по математической индукции: теория и приложения , CRC Press, стр. 240, ISBN 9781420093650
^ Jump up to: Перейти обратно: ^а ^б Эйлер, Л. (1736), «Решение проблемы, связанной с геометрией объекта» (PDF) , Commentarii Academiae Scientiarum Imperialis Petropolitana , 8 : 128–140 . Перепечатано и переведено на Биггс, Нидерланды ; Ллойд, ЕК; Уилсон, Р.Дж. (1976), Теория графов 1736–1936 , Oxford University Press
^ Jump up to: Перейти обратно: ^а ^б Хиггинс, Питер М. (1998), Математика для любознательных , Oxford University Press, стр. 201, ISBN 9780192880727
^ Jump up to: Перейти обратно: ^а ^б ^с Биггс, Норман Л. (2002), «15.3: Степень» , Дискретная математика , Oxford University Press, стр. 181–182, ISBN 9780198507178
^ Уэст, Дуглас Б. (1996), «1.3.3. Теорема. (Формула суммы степеней)», Введение в теорию графов (2-е изд.), Прентис Холл, стр. 26, ISBN 9780132278287
^ Лоер, Николас (2011), «3.31. Теорема: формула суммы степеней для орграфов» , Биективная комбинаторика , CRC Press, стр. 106, ISBN 9781439848869
^ Jump up to: Перейти обратно: ^а ^б Юкна, Стасис (2011), «Предложение 1.7», Экстремальная комбинаторика , Тексты по теоретической информатике. Серия EATCS, Springer, стр. 9, номер домена : 10.1007/978-3-642-17364-6 , ISBN 978-3-642-17363-9
^ Рэй, Сантану Саха (2012), «Теорема 2.2», Теория графов с алгоритмами и ее приложения в прикладной науке и технологиях , Springer, стр. 16, ISBN 9788132207504
^ Кристофидес, Никос (1976), Анализ наихудшего случая новой эвристики для задачи коммивояжера (PDF) , Отчет 388, Высшая школа промышленного управления, CMU, заархивировано (PDF) из оригинала 21 июля 2019 г. Лемма о рукопожатии приведена вверху страницы 2.
^ Кэмерон, Кэти; Эдмондс, Джек (1999), «Некоторые графические использования четного числа нечетных узлов» , Annales de l'Institut Fourier , 49 (3): 815–827, doi : 10.5802/aif.1694 , MR 1703426
^ Томасон, А.Г. (1978), «Гамильтоновы циклы и графы, раскрашиваемые однозначно по краям», Достижения в теории графов (Кембриджская комбинаторная конференция, Тринити-колледж, Кембридж, 1977) , Анналы дискретной математики, том. 3, стр. 259–268, doi : 10.1016/S0167-5060(08)70511-9 , MR 0499124
^ Айгнер, Мартин ; Циглер, Гюнтер М. (2018), «Раздел 28.6: Лемма Спернера», Доказательства из КНИГИ (6-е изд.), Берлин: Springer, стр. 203–205, doi : 10.1007/978-3-662-57265-8 , ISBN 978-3-662-57264-1 , МР 3823190
^ Гудман, Джейкоб Э .; Пах, Янош ; Ага, Чи-К. (1989), «Альпинизм, перемещение по лестнице и ширина кольца многоугольника» (PDF) , The American Mathematical Monthly , 96 (6): 494–510, doi : 10.2307/2323971 , JSTOR 2323971 , MR 0999412
^ Лаури, Йозеф; Скапеллато, Раффаэле (2016), Темы автоморфизмов и реконструкции графов , Серия лекций Лондонского математического общества, том. 432 (2-е изд.), Cambridge University Press, стр. 105–106, doi : 10.1017/CBO9781316669846 , ISBN 978-1-316-61044-2 , МР 3496604
^ Гейл, Дэвид (1979), «Игра в Hex и теорема Брауэра о неподвижной точке», The American Mathematical Monthly , 86 (10): 818–827, doi : 10.1080/00029890.1979.11994922 , JSTOR 2320146 , MR 0551501
^ Нето, Антонио Каминья Мунис (2018), Экскурсия по элементарной математике, Том III: Дискретная математика и полиномиальная алгебра , Сборники задач по математике, Springer, стр. 132 , 562 , ISBN 9783319779775
^ Олдос, Джоан М.; Уилсон, Робин Дж. (2000), «Теорема 2.2» , Графики и приложения: вводный подход , Серия по математике для студентов, Открытый университет, Springer-Verlag, стр. 44 , ISBN 978-1-85233-259-4
^ Уоллис, WD (2011), «Раздел 7.1, Введение в графики, следствие 1» , Руководство для начинающих по дискретной математике (2-е изд.), Springer, стр. 219, ISBN 9780817682866
^ Кларк, Джон; Холтон, Дерек Аллан (1995), «Проблема 1.4.6» , Первый взгляд на теорию графов , Allied Publishers, стр. 16, ISBN 9788170234630
^ Ловас, Ласло (2014), Комбинаторные задачи и упражнения (2-е изд.), Elsevier, стр. 281, ISBN 9780080933092
^ Пизански, Томаз ; Серватиус, Бриджит (2013), «2.3.4: Полурегулярные двудольные графы» , Конфигурации с графической точки зрения , Расширенные тексты Birkhäuser: Базельские учебники, Нью-Йорк: Birkhäuser/Springer, стр. 35, номер домена : 10.1007/978-0-8176-8364-1 , ISBN 978-0-8176-8363-4 , МР 2978043
^ Брюн, Хеннинг; Штейн, Майя (2007), «О конечных степенях и бесконечных циклах в локально конечных графах», Combinatorica , 27 (3): 269–291, doi : 10.1007/s00493-007-2149-0 , MR 2345811 , S2CID 8367713 ; см. предложение 15, с. 284
^ Каро, Яир (15 сентября 1994 г.). «О индуцированных подграфах нечетных степеней» . Дискретная математика . 132 (1–3): 23–28. дои : 10.1016/0012-365X(92)00563-7 .
^ Фербер, Асаф; Кривелевич, Михаил (2020). «Каждый граф содержит индуцированный подграф линейного размера со всеми нечетными степенями». arXiv : 2009.05495 [ math.CO ].
^ Хоннер, Патрик (24 марта 2022 г.). «Что математическая вечеринка говорит нам о теории графов» . Журнал Кванта . Проверено 27 марта 2022 г.
^ Пападимитриу, Христос Х. (1994), «О сложности аргумента четности и других неэффективных доказательствах существования», Journal of Computer and System Sciences , 48 (3): 498–532, doi : 10.1016/S0022-0000(05) )80063-7 , МР 1279412
^ Чен, Си; Дэн, Сяоте (2006), «Урегулирование сложности равновесия Нэша для двух игроков», Proc. 47-й симп. Основы информатики , стр. 261–271, doi : 10.1109/FOCS.2006.69 , S2CID 14102058 , ECCC TR05-140.
^ Гриньи, Микеланджело (2001), «Завершение леммы Спернера для PPA», Information Processing Letters , 77 (5–6): 255–259, doi : 10.1016/S0020-0190(00)00152-6 , MR 1818525
^ Филос-Рацикас, Арис; Голдберг, Пол В. (2018), «Консенсусное сокращение вдвое является PPA-полным», в Диакониколасе, Илиасе; Кемпе, Дэвид; Хензингер, Моника (ред.), Труды 50-го ежегодного симпозиума ACM SIGACT по теории вычислений, STOC 2018, Лос-Анджелес, Калифорния, США, 25–29 июня 2018 г. , стр. 51–64, arXiv : 1711.04503 , doi : 10.1145/3188745.3188880 , S2CID 8111195

[hein-1] Jump up to: Перейти обратно: ^а ^б Хейн, Джеймс Л. (2015), «Пример 3: Проблема установления связи» , Дискретные структуры, логика и вычислимость , Jones & Bartlett Publishers, стр. 703, ISBN 9781284070408

[gunderson-2] Jump up to: Перейти обратно: ^а ^б ^с Гундерсон, Дэвид С. (2014), Справочник по математической индукции: теория и приложения , CRC Press, стр. 240, ISBN 9781420093650

[euler-3] Jump up to: Перейти обратно: ^а ^б Эйлер, Л. (1736), «Решение проблемы, связанной с геометрией объекта» (PDF) , Commentarii Academiae Scientiarum Imperialis Petropolitana , 8 : 128–140 . Перепечатано и переведено на Биггс, Нидерланды ; Ллойд, ЕК; Уилсон, Р.Дж. (1976), Теория графов 1736–1936 , Oxford University Press

[higgins-4] Jump up to: Перейти обратно: ^а ^б Хиггинс, Питер М. (1998), Математика для любознательных , Oxford University Press, стр. 201, ISBN 9780192880727

[biggs-5] Jump up to: Перейти обратно: ^а ^б ^с Биггс, Норман Л. (2002), «15.3: Степень» , Дискретная математика , Oxford University Press, стр. 181–182, ISBN 9780198507178

[west-6] Уэст, Дуглас Б. (1996), «1.3.3. Теорема. (Формула суммы степеней)», Введение в теорию графов (2-е изд.), Прентис Холл, стр. 26, ISBN 9780132278287

[loehr-7] Лоер, Николас (2011), «3.31. Теорема: формула суммы степеней для орграфов» , Биективная комбинаторика , CRC Press, стр. 106, ISBN 9781439848869

[jukna-8] Jump up to: Перейти обратно: ^а ^б Юкна, Стасис (2011), «Предложение 1.7», Экстремальная комбинаторика , Тексты по теоретической информатике. Серия EATCS, Springer, стр. 9, номер домена : 10.1007/978-3-642-17364-6 , ISBN 978-3-642-17363-9

[ray-9] Рэй, Сантану Саха (2012), «Теорема 2.2», Теория графов с алгоритмами и ее приложения в прикладной науке и технологиях , Springer, стр. 16, ISBN 9788132207504

[10] Кристофидес, Никос (1976), Анализ наихудшего случая новой эвристики для задачи коммивояжера (PDF) , Отчет 388, Высшая школа промышленного управления, CMU, заархивировано (PDF) из оригинала 21 июля 2019 г. Лемма о рукопожатии приведена вверху страницы 2.

[cameron-edmonds-11] Кэмерон, Кэти; Эдмондс, Джек (1999), «Некоторые графические использования четного числа нечетных узлов» , Annales de l'Institut Fourier , 49 (3): 815–827, doi : 10.5802/aif.1694 , MR 1703426

[thomason-12] Томасон, А.Г. (1978), «Гамильтоновы циклы и графы, раскрашиваемые однозначно по краям», Достижения в теории графов (Кембриджская комбинаторная конференция, Тринити-колледж, Кембридж, 1977) , Анналы дискретной математики, том. 3, стр. 259–268, doi : 10.1016/S0167-5060(08)70511-9 , MR 0499124

[sperner-13] Айгнер, Мартин ; Циглер, Гюнтер М. (2018), «Раздел 28.6: Лемма Спернера», Доказательства из КНИГИ (6-е изд.), Берлин: Springer, стр. 203–205, doi : 10.1007/978-3-662-57265-8 , ISBN 978-3-662-57264-1 , МР 3823190

[mountain-14] Гудман, Джейкоб Э .; Пах, Янош ; Ага, Чи-К. (1989), «Альпинизм, перемещение по лестнице и ширина кольца многоугольника» (PDF) , The American Mathematical Monthly , 96 (6): 494–510, doi : 10.2307/2323971 , JSTOR 2323971 , MR 0999412

[lausca-15] Лаури, Йозеф; Скапеллато, Раффаэле (2016), Темы автоморфизмов и реконструкции графов , Серия лекций Лондонского математического общества, том. 432 (2-е изд.), Cambridge University Press, стр. 105–106, doi : 10.1017/CBO9781316669846 , ISBN 978-1-316-61044-2 , МР 3496604

[gale-16] Гейл, Дэвид (1979), «Игра в Hex и теорема Брауэра о неподвижной точке», The American Mathematical Monthly , 86 (10): 818–827, doi : 10.1080/00029890.1979.11994922 , JSTOR 2320146 , MR 0551501

[neto-17] Нето, Антонио Каминья Мунис (2018), Экскурсия по элементарной математике, Том III: Дискретная математика и полиномиальная алгебра , Сборники задач по математике, Springer, стр. 132 , 562 , ISBN 9783319779775

[aldous-wilson-18] Олдос, Джоан М.; Уилсон, Робин Дж. (2000), «Теорема 2.2» , Графики и приложения: вводный подход , Серия по математике для студентов, Открытый университет, Springer-Verlag, стр. 44 , ISBN 978-1-85233-259-4

[wallis-19] Уоллис, WD (2011), «Раздел 7.1, Введение в графики, следствие 1» , Руководство для начинающих по дискретной математике (2-е изд.), Springer, стр. 219, ISBN 9780817682866

[clahol-20] Кларк, Джон; Холтон, Дерек Аллан (1995), «Проблема 1.4.6» , Первый взгляд на теорию графов , Allied Publishers, стр. 16, ISBN 9788170234630

[lovasz-21] Ловас, Ласло (2014), Комбинаторные задачи и упражнения (2-е изд.), Elsevier, стр. 281, ISBN 9780080933092

[configs-22] Пизански, Томаз ; Серватиус, Бриджит (2013), «2.3.4: Полурегулярные двудольные графы» , Конфигурации с графической точки зрения , Расширенные тексты Birkhäuser: Базельские учебники, Нью-Йорк: Birkhäuser/Springer, стр. 35, номер домена : 10.1007/978-0-8176-8364-1 , ISBN 978-0-8176-8363-4 , МР 2978043

[bruhnstein-23] Брюн, Хеннинг; Штейн, Майя (2007), «О конечных степенях и бесконечных циклах в локально конечных графах», Combinatorica , 27 (3): 269–291, doi : 10.1007/s00493-007-2149-0 , MR 2345811 , S2CID 8367713 ; см. предложение 15, с. 284

[24] Каро, Яир (15 сентября 1994 г.). «О индуцированных подграфах нечетных степеней» . Дискретная математика . 132 (1–3): 23–28. дои : 10.1016/0012-365X(92)00563-7 .

[25] Фербер, Асаф; Кривелевич, Михаил (2020). «Каждый граф содержит индуцированный подграф линейного размера со всеми нечетными степенями». arXiv : 2009.05495 [ math.CO ].

[26] Хоннер, Патрик (24 марта 2022 г.). «Что математическая вечеринка говорит нам о теории графов» . Журнал Кванта . Проверено 27 марта 2022 г.

[papadimitriou-27] Пападимитриу, Христос Х. (1994), «О сложности аргумента четности и других неэффективных доказательствах существования», Journal of Computer and System Sciences , 48 (3): 498–532, doi : 10.1016/S0022-0000(05) )80063-7 , МР 1279412

[chen-deng-28] Чен, Си; Дэн, Сяоте (2006), «Урегулирование сложности равновесия Нэша для двух игроков», Proc. 47-й симп. Основы информатики , стр. 261–271, doi : 10.1109/FOCS.2006.69 , S2CID 14102058 , ECCC TR05-140.

[grigni-29] Гриньи, Микеланджело (2001), «Завершение леммы Спернера для PPA», Information Processing Letters , 77 (5–6): 255–259, doi : 10.1016/S0020-0190(00)00152-6 , MR 1818525

[filgol-30] Филос-Рацикас, Арис; Голдберг, Пол В. (2018), «Консенсусное сокращение вдвое является PPA-полным», в Диакониколасе, Илиасе; Кемпе, Дэвид; Хензингер, Моника (ред.), Труды 50-го ежегодного симпозиума ACM SIGACT по теории вычислений, STOC 2018, Лос-Анджелес, Калифорния, США, 25–29 июня 2018 г. , стр. 51–64, arXiv : 1711.04503 , doi : 10.1145/3188745.3188880 , S2CID 8111195

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]