Проблема альпинизма

Тривиальный пример.

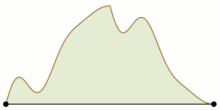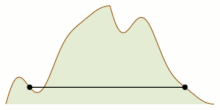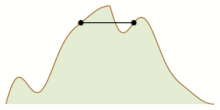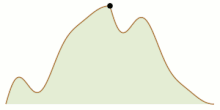
В математике задача альпинизма — это математическая задача , которая рассматривает двумерный горный хребет (представленный как непрерывная функция ) и спрашивает, возможно ли, чтобы два альпиниста начинали на уровне моря с левой и правой стороны горы. встретиться на вершине, всегда сохраняя одинаковую высоту. Эта проблема была названа и поставлена ​​в такой форме Джеймсом В. Уиттакером ( 1966 ), но ее история восходит к Тацуо Хомме ( 1952 ), который решил одну из ее версий. Проблема неоднократно открывалась заново и решалась независимо в разных контекстах рядом людей (см. ссылки ниже).

С 1990-х годов было показано, что проблема связана со слабым расстоянием Фреше на кривых плоскости: различные планирования плоского движения задачи в вычислительной геометрии , задача о вписанном квадрате , полугруппа полиномов ​ , и т. д. Проблема была популяризирована в статье Гудмана, Пача и Япа (1989) , получившей Математической ассоциации Америки в 1990 году. премию Лестера Р. Форда от

Анализ

Проблему можно перефразировать так: может ли для данной пары непрерывных функций $f,g$ с $f(0)=g(0)=0,f(1)=g(1)=1$ (соответствует масштабированным версиям левой и правой граней горы), можно найти другую пару функций $x_{1},x_{2}$ с $x_{1}(0)=x_{2}(0)=0,x_{1}(1)=x_{2}(1)=1$ (горизонтальные положения альпинистов в момент времени $t$) такие, что композиции функций $f\circ x_{1}$ и $g\circ x_{2}$ (высоты альпинистов в момент времени $t$) — это одна и та же функция.

Конечное число вершин и долин.

Пример, требующий возврата. Исходное изображение представляет собой анимированный SVG; нажмите, чтобы просмотреть его.

Когда $f,g$ Имея лишь конечное число вершин и впадин ( локальных максимумов и локальных минимумов ), всегда можно координировать движения альпинистов. Это можно продемонстрировать, нарисовав своего рода дерево игры : неориентированный граф. $G$ с одной вершиной, помеченной $(x_{1},x_{2})$ в любое время $f(x_{1})=g(x_{2})$ и либо $f(x_{1})$ или $g(x_{2})$ является локальным максимумом или минимумом. Две вершины будут соединены ребром тогда и только тогда, когда один узел сразу достижим из другого; степень вершины будет больше единицы только тогда, когда альпинистам придется сделать нетривиальный выбор из этой позиции.

• В вершине $(0,0)$, степень одна: единственное возможное направление движения обоих альпинистов — на гору. Аналогично, в $(1,1)$ степень равна единице, потому что оба альпиниста могут вернуться только вниз с горы.
• В вершине, где один альпинист находится на вершине или в долине, а другой нет, тогда степень равна двум: у альпиниста на вершине или в долине есть два выбора, каким путем идти, а другой альпинист может пойти только одним. способ.
• В вершине, где оба альпиниста находятся на вершине или оба альпиниста находятся в долине, степень равна четырем: оба альпиниста могут независимо друг от друга выбирать, в каком направлении идти.
• В вершине, где один альпинист находится на вершине, а другой в долине, степень равна нулю: такие позиции недостижимы. (Т.е. если такая вершина существует, то граф $G$ не подключен .)

Согласно лемме о квитировании , каждая компонента связности неориентированного графа имеет четное количество вершин нечетной степени. Поскольку единственные вершины нечетной степени во всем $G$ являются $(0,0)$ и $(1,1)$, эти две вершины должны принадлежать одной и той же компоненте связности. То есть, $G$ должен содержать путь от $(0,0)$ к $(1,1)$. Этот путь подсказывает, как координировать движение альпинистов к вершине.

Было замечено, что для горы с n вершинами и долинами длина этого пути (примерно соответствующая количеству раз, когда тот или иной альпинист должен «вернуться назад») может быть даже квадратичной по n .

Эта техника выходит из строя, когда $f,g$ иметь бесконечное число локальных экстремумов. В этом случае $G$ не будет конечным графом, поэтому лемма о установлении связи не будет применяться: $(0,0)$ и $(1,1)$ могут быть связаны, но только путем с бесконечным числом вершин, возможно, для прохождения альпинистам потребуется «бесконечное время».

Бесконечное количество вершин и долин.

Следующий результат принадлежит Хунеке (1969) :

Предполагать $f$ и $g$ являются непрерывными функциями из $[0,1]$ к $[0,1]$ с $f(0)=g(0)=0$ и $f(1)=g(1)=1$, и такой, что ни одна из функций не является постоянной на интервале . Тогда существуют непрерывные функции $s$ и $t$ от $[0,1]$ к $[0,1]$ с $s(0)=t(0)=0$, $s(1)=t(1)=1$, и такой, что $f\circ s\,=\,g\circ t$, где " $\circ$" означает композицию функций .

С другой стороны, невозможно распространить этот результат на все непрерывные функции. Ибо, если $f$ имеет постоянную высоту на интервале, в то время как $g$ имеет бесконечно много колебаний, проходящих через одну и ту же высоту, то первый альпинист может быть вынужден идти вперед и назад на этом интервале бесконечно много раз, делая его путь к вершине бесконечно длинным. Джеймс В. Уиттакер ( 1966 ) приводит конкретный пример, включающий $x\sin(x^{-1})$.

Ссылки

• Бэрд, Б.Б.; Мэгилл, К.Д. младший (1997), "Грин" ${\mathcal {R}}$, ${\mathcal {D}}$ и ${\mathcal {H}}$ отношения для обобщенных полиномов», Semigroup Forum , 55 (3): 267–293, doi : 10.1007/PL00005929 , MR   1469444 , S2CID   120449490 .
• Бучин, Кевин; Бучин, Майке ; Кнауэр, Кристиан; Роте, Гюнтер; Венк, Карола (2007), «Насколько сложно выгуливать собаку?» , учеб. 23-й Европейский семинар по вычислительной геометрии (Грац, 2007 г.) , стр. 170–173 .
• Гудман, Джейкоб Э .; Пах, Янош ; Ага, Чи-К. (1989), «Альпинизм, перемещение по лестнице и ширина кольца многоугольника» (PDF) , American Mathematical Monthly , 96 (6): 494–510, doi : 10.2307/2323971 , JSTOR   2323971 , MR   0999412 .
• Хомма, Тацуо (1952), «Теорема о непрерывных функциях», Отчеты математического семинара Кодай , 4 : 13–16, doi : 10.2996/kmj/1138843207 , MR   0049988 .
• Хунеке, Джон Филип (1969), «Альпинизм», Труды Американского математического общества , 139 : 383–391, doi : 10.2307/1995331 , JSTOR   1995331 , MR   0239013 .
• Хименес Лопес, Виктор (1999), «Элементарное решение проблемы альпинистов», Mathematical Equations , 57 (1): 45–49, doi : 10.1007/s000100050069 , MR   1675749 , S2CID   121912365 .
• Келети, Тамаш (1993), «Проблема альпинистов», Proceedings of the American Mathematical Society , 117 (1): 89–97, doi : 10.2307/2159702 , JSTOR   2159702 , MR   1123655 .
• Липинский, Дж. С. (1957), “Об униформизации непрерывных функций”, Bull. акад. Полон. наук. Кл. III , 5 : 1019–1021, LXXXV, MR   0095224 .
• Маккирнан, Массачусетс (1985), «Альпинизм: альтернативное доказательство», Aequationes Mathematicae , 28 (1–2): 132–134, doi : 10.1007/BF02189402 , MR   0781218 , S2CID   120938782 .
• Миодушевский, Дж. (1962), «О квазиупорядочении в классе непрерывных отображений замкнутого интервала в себя», Colloquium Mathematicum , 9 (2): 233–240, doi : 10.4064/cm-9-2- 233-240 , МР   0143181 .
• Пак, Игорь (2010), Лекции по дискретной и многогранной геометрии , с. 39 .
• Сикорский, Р.; Заранкевич, К. (1955), «Об униформизации функций. I», Fundamenta Mathematicae , 41 (2): 339–344, doi : 10.4064/fm-41-2-339-344 , MR   0072465 .
• Такер, Алан (1995), «Загадка параллельных альпинистов» (PDF) , Math Horizons , 3 (2): 22–24, doi : 10.1080/10724117.1995.11974954 .
• Уиттакер, Джеймс В. (1966), «Задача альпинизма», Canadian Journal of Mathematics , 18 : 873–882, doi : 10.4153/CJM-1966-087-x , MR   0196013 , S2CID   124117059 ..

Внешние ссылки

• Задача параллельных альпинистов , описание и решение Java-апплета .