Расстояние Фреше

В математике расстояние Фреше — это мера сходства между кривыми , которая учитывает расположение и порядок точек вдоль кривых. Он назван в честь Мориса Фреше .

Интуитивное определение

Представьте себе человека, пересекающего конечный изогнутый путь, выгуливающего свою собаку на поводке, при этом собака пересекает отдельный конечный изогнутый путь. Каждый из них может изменять свою скорость, чтобы не ослаблять поводок, но ни один из них не может двигаться назад. Расстояние Фреше между двумя кривыми — это длина кратчайшего поводка, достаточная для того, чтобы оба могли пройти свои отдельные пути от начала до конца. Обратите внимание, что определение симметрично относительно двух кривых: расстояние Фреше было бы таким же, если бы собака выгуливала своего хозяина.

Формальное определение

Позволять $S$ быть метрическим пространством . Кривая $A$ в $S$ представляет собой непрерывное отображение единичного интервала в $S$ , то есть, $A:[0,1]\rightarrow S$ . Репараметризация $\alpha$ из $[0,1]$ непрерывную неубывающую сюръекцию представляет собой $\alpha :[0,1]\rightarrow [0,1]$ .

Позволять $A$ и $B$ быть двумя заданными кривыми в $S$ . Тогда расстояние Фреше между $A$ и $B$ определяется как нижняя грань по всем перепараметризациям $\alpha$ и $\beta$ из $[0,1]$ максимум из всех $t\in [0,1]$ расстояния в $S$ между $A(\alpha (t))$ и $B(\beta (t))$ . В математических обозначениях расстояние Фреше $F(A,B)$ является

$F(A,B)=\inf _{\alpha ,\beta }\,\,\max _{t\in [0,1]}\,\,{\biggl \{}d{\Bigl (}A{\bigl (}\alpha (t){\bigr )},\,B{\bigl (}\beta (t){\bigr )}{\Bigr )}{\biggr \}}$

где $d$ является расстояния функцией $S$ .

Неформально мы можем думать о параметре $t$ как «время». Затем, $A(\alpha (t))$ это положение собаки и $B(\beta (t))$ это позиция владельца собаки в данный момент $t$ (или наоборот). Длина поводка между ними во времени $t$ это расстояние между $A(\alpha (t))$ и $B(\beta (t))$ . Взяв нижнюю границу по всем возможным репараметризациям $[0,1]$ соответствует выбору прогулки по заданным путям, при которой максимальная длина поводка минимальна. Ограничение, которое $\alpha$ и $\beta$ быть неубывающим означает, что ни собака, ни ее хозяин не могут попятиться.

Метрика Фреше учитывает течение двух кривых, поскольку пары точек, расстояние до которых способствует расстоянию Фреше, непрерывно перемещаются вдоль соответствующих кривых. Это делает расстояние Фреше лучшей мерой сходства кривых, чем альтернативы, такие как расстояние Хаусдорфа , для произвольных наборов точек. Две кривые могут иметь небольшое расстояние Хаусдорфа, но большое расстояние Фреше.

Расстояние Фреше и его варианты находят применение в нескольких задачах, от морфинга ^{[ 1 ]} и распознавание рукописного ввода ^{[ 2 ]} выравниванию структуры белка . ^{[ 3 ]} Альт и коды ^{[ 4 ]} были первыми, кто описал алгоритм с полиномиальным временем для вычисления расстояния Фреше между двумя ломаными кривыми в евклидовом пространстве , основанный на принципе параметрического поиска . Время работы их алгоритма $O(mn\cdot \log(mn))$ для двух ломаных с m и n сегментами.

Диаграмма свободного пространства

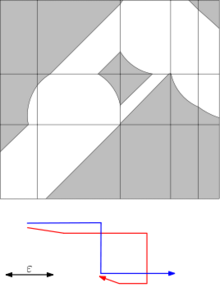
пример диаграммы свободного пространства — Диаграмма красной и синей кривой в свободном пространстве. В отличие от определения в тексте, в котором для обеих кривых используется интервал параметров [0,1], в этом примере кривые параметризуются длиной дуги.

Важным инструментом для расчета расстояния Фреше двух кривых является диаграмма свободного пространства, введенная Альтом и Годау. ^{[ 4 ]} Диаграмма свободного пространства между двумя кривыми для заданного порога расстояния ε представляет собой двумерную область в пространстве параметров, состоящую из всех пар точек на двух кривых на расстоянии не более ε:

$D_{\varepsilon }(A,B):={\bigl \{}(\alpha ,\beta )\in [0,1]^{2}\mathbin {\big |} d(A(\alpha ),B(\beta ))\leq \varepsilon {\bigr \}}$

Расстояние Фреше $F(A,B)$ не превосходит ε тогда и только тогда, когда диаграмма свободного пространства $D_{\varepsilon }(A,B)$ содержит путь от левого нижнего угла до правого верхнего угла, монотонный как в горизонтальном, так и в вертикальном направлении.

Как расстояние между распределениями вероятностей (оценка FID)

Помимо измерения расстояний между кривыми, расстояние Фреше также можно использовать для измерения разницы между распределениями вероятностей .

Для двух многомерных гауссовских распределений со средними значениями $\mu _{X}$ и $\mu _{Y}$ и ковариационные матрицы $\Sigma _{X}$ и $\Sigma _{Y}$ , расстояние Фреше между этими распределениями равно $d$ данный ^{[ 5 ]}

$d^{2}=|\mu _{X}-\mu _{Y}|^{2}+\operatorname {tr} (\Sigma _{X}+\Sigma _{Y}-2(\Sigma _{X}\Sigma _{Y})^{1/2})$ .

Это расстояние является основой начального расстояния Фреше (FID), которое используется для сравнения изображений, созданных генеративно-состязательной сетью , с реальными изображениями, которые использовались для обучения.

Варианты

Слабое расстояние Фреше представляет собой вариант классического расстояния Фреше без требования, чтобы конечные точки двигались монотонно вдоль соответствующих кривых: собаке и ее владельцу разрешено отступать, чтобы поводок между ними был коротким. Альт и Годау ^{[ 4 ]} описать более простой алгоритм вычисления слабого расстояния Фреше между ломаными кривыми, основанный на вычислении минимаксных путей в связанном сеточном графе .

Дискретное расстояние Фреше , также называемое расстоянием связи , является аппроксимацией метрики Фреше для ломаных кривых, определенной Эйтером и Маннилой. ^{[ 6 ]} Дискретное расстояние Фреше учитывает только те положения поводка, где его конечные точки расположены в вершинах двух ломаных кривых, и никогда — внутри ребра. Это приближение безоговорочно дает большие значения, чем соответствующее (непрерывное) расстояние Фреше. Однако погрешность аппроксимации ограничена наибольшим расстоянием между двумя соседними вершинами ломаных кривых. В отличие от обычных алгоритмов (непрерывного) расстояния Фреше, этот алгоритм не зависит от мер расстояния, индуцированных метрическим пространством. Ее формулировка как задача динамического программирования может быть эффективно реализована с квадратичным временем выполнения и линейными затратами памяти, используя всего несколько строк кода. ^{[ 7 ]}

Когда две кривые встроены в метрическое пространство, отличное от евклидова, например, в многогранную местность или в какое-то евклидово пространство с препятствиями, расстояние между двумя точками на кривых наиболее естественно определяется как длина кратчайшего пути между ними. Привязь должна представлять собой геодезическую, соединяющую ее конечные точки. Полученная метрика между кривыми называется геодезическим расстоянием Фреше . ^{[ 1 ]}^{[ 8 ]}^{[ 9 ]} Кук и Венк ^{[ 8 ]} описать алгоритм с полиномиальным временем для вычисления геодезического расстояния Фреше между двумя ломаными кривыми в простом многоугольнике .

Если мы далее потребуем, чтобы поводок двигался непрерывно в окружающем метрическом пространстве, то мы получим понятие гомотопического расстояния Фреше ^{[ 10 ]} между двумя кривыми. Поводок не может прерывисто переключаться из одного положения в другое — в частности, поводок не может перепрыгивать препятствия, а перемахивать гору на местности может только в том случае, если он достаточно длинный. Движение поводка описывает гомотопию между двумя кривыми. Чемберс и др. ^{[ 10 ]} описать алгоритм с полиномиальным временем для вычисления гомотопического расстояния Фреше между ломаными кривыми на евклидовой плоскости с препятствиями.

Примеры

Расстояние Фреше между двумя концентрическими кругами радиуса $r_{1}$ и $r_{2}$ соответственно $|r_{1}-r_{2}|.$ Самый длинный поводок необходим, когда хозяин стоит на месте, а собака переходит на противоположную сторону круга ( $r_{1}+r_{2}$ ), и самый короткий поводок, когда и хозяин, и собака ходят с постоянной угловой скоростью по кругу ( $|r_{1}-r_{2}|$ ).

Приложения

Расстояние Фреше использовалось для изучения визуальной иерархии — принципа графического дизайна. ^{[ 11 ]}

См. также

Ссылки

^ Jump up to: ^а ^б Эфрат, Алон; Гибас, Леонидас Дж .; Хар-Пелед, Сариэль ; Митчелл, Джозеф С.Б .; Мурали, Т.М. (2002), «Новые меры сходства между полилиниями с применением к морфированию и вытягиванию полигонов» (PDF) , Discrete and Computational Geometry , 28 (4): 535–569, doi : 10.1007/s00454-002-2886-1 , S2CID 16382161 , заархивировано из оригинала (PDF) от 19 июня 2010 г. , получено 7 августа 2010 г.
^ Шрирагхавендра, Р.; Картик, К.; Бхаттачарья, Чиранджиб (2007), «Расстояние Фреше для поиска рукописных документов в Интернете», Proc. 9-я Международная конференция по анализу и распознаванию документов (ICDAR '07) , стр. 461–465, doi : 10.1109/ICDAR.2007.121 , S2CID 2533396 .
^ Минхуэй, Цзян; Ин, Сюй; Биньхай, Чжу (2008), «Выравнивание структуры-структуры белка с дискретным расстоянием Фреше» (PDF) , Журнал биоинформатики и вычислительной биологии , 6 (1): 51–64, doi : 10.1142/S0219720008003278 , PMID 18324745 .
^ Jump up to: ^а ^б ^с Альт, Хельмут ; Годау, Майкл (1995), «Вычисление расстояния Фреше между двумя многоугольными кривыми» (PDF) , Международный журнал вычислительной геометрии и приложений , 5 (1–2): 75–91, doi : 10.1142/S0218195995000064 .
^ Доусон, округ Колумбия; Ландау, Б.В. (1 сентября 1982 г.). «Расстояние Фреше между многомерными нормальными распределениями» . Журнал многомерного анализа . 12 (3): 450–455. дои : 10.1016/0047-259X(82)90077-X . ISSN 0047-259X .
^ Эйтер, Томас; Маннила, Хейкки (1994), Вычисление дискретного расстояния Фреше (PDF) , Tech. Отчет CD-TR 94/64, Лаборатория Кристиана Доплера экспертных систем, Венский технический университет, Австрия .
^ Мейнерт, Нис. «Быстрая прогулка по лягушке в 4 LoC» . arXiv . Проверено 9 апреля 2024 г.
^ Jump up to: ^а ^б Кук, Атлас Ф. IV; Венк, Карола (2008), Геодезическое расстояние Фреше с многоугольными препятствиями (PDF) , Tech. Отчет CS-TR-2008-0010, Техасский университет в Сан-Антонио .
^ Махешвари, Анил; Йи, Цзехуа (2005), «О вычислении расстояния Фреше двух путей на выпуклом многограннике», Proc. 21-й европейский семинар по вычислительной геометрии (PDF) , стр. 41–44 .
^ Jump up to: ^а ^б Чемберс, Эрин Вольф; Колен де Вердьер, Эрик; Эриксон, Джефф; Лазар, Сильвен; Лазарь, Фрэнсис; Тайт, Шрипад (2009), «Гомотопическое расстояние Фреше между кривыми, или Прогулка с собакой в лесу за полиномиальное время» (PDF) , Вычислительная геометрия: теория и приложения , 43 (3): 295–311, doi : 10.1016/j .comgeo.2009.02.008 , S2CID 124507726 .
^ Урано, Йоко; Куросу, Аарон; Хенсельман-Петрусек, Грегори; Тодоров, Александр (2021). «Визуальная иерархия связана с впечатлением от хорошего дизайна» . Семинар CHI'21 по движениям глаз как интерфейсу когнитивного состояния : 1–9. doi : 10.31234/osf.io/hksf9 . S2CID 236599584 .

Дальнейшее чтение

де Берг, Марк, «Анализ траекторий движущихся объектов», Вычислительная геометрия, Две избранные темы (PDF) , стр. 11–75 .
Аронов, Борис ; Хар-Пелед, Сариэль; Кнауэр, Кристиан; Ван, Юсу ; Венк, Карола (2006), «Расстояние Фреше для кривых, пересмотренный», Алгоритмы – ESA 2006 (PDF) , Конспекты лекций по информатике, том. 4168, Шпрингер-Верлаг, стр. 52–63, arXiv : 1504.07685 , doi : 10.1007/11841036_8 , ISBN 978-3-540-38875-3 , S2CID 9286354 , заархивировано из оригинала (PDF) 12 июня 2010 г.
Альт, Хельмут ; Бучин, Майке (2010), «Можем ли мы вычислить сходство между поверхностями?», Дискретная и вычислительная геометрия , 43 : 78–99, arXiv : cs.CG/0703011 , doi : 10.1007/s00454-009-9152-8 , S2CID 5799576 .

[efrat02new-1] Jump up to: ^а ^б Эфрат, Алон; Гибас, Леонидас Дж .; Хар-Пелед, Сариэль ; Митчелл, Джозеф С.Б .; Мурали, Т.М. (2002), «Новые меры сходства между полилиниями с применением к морфированию и вытягиванию полигонов» (PDF) , Discrete and Computational Geometry , 28 (4): 535–569, doi : 10.1007/s00454-002-2886-1 , S2CID 16382161 , заархивировано из оригинала (PDF) от 19 июня 2010 г. , получено 7 августа 2010 г.

[sri07frechet-2] Шрирагхавендра, Р.; Картик, К.; Бхаттачарья, Чиранджиб (2007), «Расстояние Фреше для поиска рукописных документов в Интернете», Proc. 9-я Международная конференция по анализу и распознаванию документов (ICDAR '07) , стр. 461–465, doi : 10.1109/ICDAR.2007.121 , S2CID 2533396 .

[minghui08protein-3] Минхуэй, Цзян; Ин, Сюй; Биньхай, Чжу (2008), «Выравнивание структуры-структуры белка с дискретным расстоянием Фреше» (PDF) , Журнал биоинформатики и вычислительной биологии , 6 (1): 51–64, doi : 10.1142/S0219720008003278 , PMID 18324745 .

[alt95frechet-4] Jump up to: ^а ^б ^с Альт, Хельмут ; Годау, Майкл (1995), «Вычисление расстояния Фреше между двумя многоугольными кривыми» (PDF) , Международный журнал вычислительной геометрии и приложений , 5 (1–2): 75–91, doi : 10.1142/S0218195995000064 .

[gaussian-5] Доусон, округ Колумбия; Ландау, Б.В. (1 сентября 1982 г.). «Расстояние Фреше между многомерными нормальными распределениями» . Журнал многомерного анализа . 12 (3): 450–455. дои : 10.1016/0047-259X(82)90077-X . ISSN 0047-259X .

[eiter94discrete-6] Эйтер, Томас; Маннила, Хейкки (1994), Вычисление дискретного расстояния Фреше (PDF) , Tech. Отчет CD-TR 94/64, Лаборатория Кристиана Доплера экспертных систем, Венский технический университет, Австрия .

[7] Мейнерт, Нис. «Быстрая прогулка по лягушке в 4 LoC» . arXiv . Проверено 9 апреля 2024 г.

[cook08geodesic-8] Jump up to: ^а ^б Кук, Атлас Ф. IV; Венк, Карола (2008), Геодезическое расстояние Фреше с многоугольными препятствиями (PDF) , Tech. Отчет CS-TR-2008-0010, Техасский университет в Сан-Антонио .

[maheshwari05frechet-9] Махешвари, Анил; Йи, Цзехуа (2005), «О вычислении расстояния Фреше двух путей на выпуклом многограннике», Proc. 21-й европейский семинар по вычислительной геометрии (PDF) , стр. 41–44 .

[chambers09homotopic-10] Jump up to: ^а ^б Чемберс, Эрин Вольф; Колен де Вердьер, Эрик; Эриксон, Джефф; Лазар, Сильвен; Лазарь, Фрэнсис; Тайт, Шрипад (2009), «Гомотопическое расстояние Фреше между кривыми, или Прогулка с собакой в лесу за полиномиальное время» (PDF) , Вычислительная геометрия: теория и приложения , 43 (3): 295–311, doi : 10.1016/j .comgeo.2009.02.008 , S2CID 124507726 .

[11] Урано, Йоко; Куросу, Аарон; Хенсельман-Петрусек, Грегори; Тодоров, Александр (2021). «Визуальная иерархия связана с впечатлением от хорошего дизайна» . Семинар CHI'21 по движениям глаз как интерфейсу когнитивного состояния : 1–9. doi : 10.31234/osf.io/hksf9 . S2CID 236599584 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]