тема Спернера

Двумерный случай леммы Спернера: раскраска Спернера с заштрихованными трехцветными треугольниками.

В математике — лемма Спернера комбинаторный результат о раскрасках триангуляций , аналогичный теореме Брауэра о неподвижной точке . эквивалентной ей ^{[ 1 ]} Он утверждает, что каждая раскраска Спернера (описанная ниже) триангуляции $n$ -мерный симплекс содержит ячейку, все вершины которой имеют разные цвета.

Первоначальный результат такого рода был доказан Эмануэлем Спернером в связи с доказательствами инвариантности области определения . Раскраски Спернера использовались для эффективного вычисления фиксированных точек и в алгоритмах поиска корней , а также применяются в алгоритмах справедливого дележа (разрезания торта).

Согласно Советской математической энциклопедии (под ред. И. М. Виноградова ), родственная теорема 1929 г. ( Кнастера , Борсука и Мазуркевича ) стала также известна как лемма Шпернера — этот момент обсуждается в английском переводе (под ред. М. Хазевинкеля). Сейчас она широко известна как лемма Кнастера-Куратовского-Мазуркевича .

Заявление

Одномерный случай

Пример одномерного случая

В одном измерении лемму Спернера можно рассматривать как дискретную версию теоремы о промежуточном значении . В данном случае по сути это говорит о том, что если дискретная функция принимает только значения 0 и 1, начинается со значения 0 и заканчивается значением 1, то она должна переключать значения нечетное число раз.

Двумерный случай

Чаще всего упоминается двумерный случай. Об этом говорится следующим образом:

Разобьем треугольник $ABC$ произвольно на триангуляцию, состоящую из меньших треугольников, соприкасающихся ребрами. Тогда раскраска Спернера триангуляции определяется как присвоение вершинам триангуляции трех цветов такое, что

Каждая из трех вершин $A$ , $B$ и $C$ исходного треугольника имеет свой цвет.
Вершины, лежащие на любом ребре треугольника $ABC,$ имеют только два цвета: два цвета на концах ребра. Например, каждая вершина $AC$ должна иметь тот же цвет, что $A$ или $C.$ и

Тогда каждая раскраска Спернера каждой триангуляции имеет по крайней мере один «радужный треугольник», меньший треугольник в триангуляции, вершины которого окрашены во все три разных цвета. Точнее, радужных треугольников должно быть нечетное количество.

Многомерный случай

В общем случае лемма относится к $n$ -мерному симплексу :

{\mathcal {A}}=A_{1}A_{2}\ldots A_{n+1}.

Рассмотрим любую триангуляцию $T$ , непересекающееся деление ${\mathcal {A}}$ на меньшие $n$ -мерные симплексы, снова встречающиеся лицом к лицу. Обозначим функцию окраски как:

f:S\to \{1,2,3,\dots ,n,n+1\},

где $S$ — множество вершин $T$ . Функция раскраски определяет раскраску Спернера, когда:

Вершины большого симплекса раскрашены в разные цвета, то есть без ограничения общности $f (A i) = i$ для $1 \leq i \leq n + 1$ .
Вершины графа $T,$ расположенные на любой $k$ -мерной подграни большого симплекса
$A_{i_{1}}A_{i_{2}}\ldots A_{i_{k+1}}$
окрашены только цветами
$i_{1},i_{2},\ldots ,i_{k+1}.$

Тогда каждая раскраска Спернера каждой триангуляции $n$ -мерного симплекса имеет нечетное количество экземпляров радужного симплекса , то есть симплекса, вершины которого окрашены во все $n + 1$ цвет. В частности, должен существовать хотя бы один радужный симплекс.

Доказательства

Доказательство по индукции

Сначала мы рассмотрим двумерный случай. Рассмотрим граф $G,$ построенный из триангуляции $T$ следующим образом:

Вершины

G

— это члены

T

плюс площадь вне треугольника. Две вершины соединены ребром, если их соответствующие области имеют общую границу, причем одна конечная точка окрашена в цвет 1, а другая - в цвет 2.

Обратите внимание, что на интервале $AB$ имеется нечетное количество границ, окрашенных в цвета 1-2 (просто потому, что A окрашено в цвет 1, B — в цвет 2; и при движении по $AB$ должно произойти нечетное количество изменений цвета, чтобы получить разные цвета в начале и в конце). На интервалах BC и CA границ цвета 1-2 вообще нет. Следовательно, вершина $G,$ соответствующая внешней области, имеет нечетную степень. Но известно ( лемма о рукопожатии ), что в конечном графе имеется четное число вершин нечетной степени. Следовательно, оставшийся граф, исключая внешнюю область, имеет нечетное количество вершин нечетной степени, соответствующих членам $T$ .

Легко видеть, что единственная возможная степень треугольника из $T$ равна 0, 1 или 2 и что степень 1 соответствует треугольнику, окрашенному в три цвета 1, 2 и 3.

Таким образом, мы получили несколько более сильный вывод, который говорит, что в триангуляции $Т$ имеется нечетное число (и хотя бы один) полноцветных треугольников.

Многомерный случай можно доказать индукцией по размерности симплекса. Применим те же рассуждения, что и в двумерном случае, чтобы заключить, что в $n$ -мерной триангуляции имеется нечетное число полноцветных симплексов.

Комментарий

Простая двумерная триангуляция примера фигуры, раскрашенная и названная в соответствии с предположениями леммы Спернера.

График, полученный на основе рисунка-примера

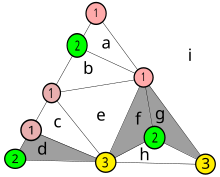
Вот развитие доказательства, данного ранее, для читателя, плохо знакомого с теорией графов .

На этой диаграмме пронумерованы цвета вершин приведенного ранее примера. Маленькие треугольники, все вершины которых имеют разные номера, на графике заштрихованы. Каждый маленький треугольник становится узлом нового графа, полученного в результате триангуляции. Маленькие буквы обозначают области: восемь внутри фигуры, а область $i$ обозначает пространство за ее пределами.

Как описано ранее, те узлы, которые имеют общее ребро, конечные точки которого пронумерованы 1 и 2, соединяются в производном графе. Например, узел $d$ имеет общее ребро с внешней областью $i$ , и все его вершины имеют разные номера, поэтому он также заштрихован. Узел $b$ не закрашен, поскольку две вершины имеют одинаковый номер, но он соединен с внешней областью.

Можно добавить новый треугольник с полным номером, скажем, вставив узел с номером 3 в ребро между 1 и 1 узла $a$ и присоединив этот узел к другой вершине $a$ . Для этого потребуется создать пару новых узлов, как в случае с узлами $f$ и $g$ .

Доказательство без индукции

Эндрю МакЛеннан и Раби Турки представили другое доказательство, используя объем симплекса . Это происходит в один этап, без индукции. ^{[ 2 ]}^{[ 3 ]}

Вычисления стали проще благодаря Спернеру

Предположим, что существует d -мерный симплекс с длиной стороны N и он триангулирован на подсимплексы с длиной стороны 1. Существует функция, которая по любой вершине триангуляции возвращает ее цвет. Раскраска гарантированно удовлетворяет граничному условию Спернера. Сколько раз нам нужно вызвать функцию, чтобы найти радужный симплекс? Очевидно, мы можем перебрать все вершины триангуляции, число которых равно O( N ^д), который является полиномиальным по N при фиксированной размерности. Но можно ли это сделать за время O(poly(log N )), которое является полиномиальным в двоичном представлении N?

Эту проблему впервые изучил Христос Пападимитриу . Он ввел класс сложности под названием PPAD , который содержит эту, а также связанные с ней задачи (например, поиск фиксированной точки Брауэра ). Он доказал, что нахождение симплекса Спернера является PPAD-полным даже при d =3. Примерно 15 лет спустя Чен и Дэн доказали PPAD-полноту даже для d =2. ^{[ 4 ]} Считается, что PPAD-сложные задачи не могут быть решены за время O(poly(log N )).

Обобщения

Подмножества этикеток

Предположим, что каждая вершина триангуляции может быть помечена несколькими цветами, так что функция окраски равна $F : S \to 2. [н +1]$ .

Для каждого подсимплекса набор меток на его вершинах представляет собой семейство множеств над набором цветов $[n + 1]$ . Это семейство множеств можно рассматривать как гиперграф .

Если для каждой вершины $v$ на грани симплекса цвета в $f (v)$ являются подмножеством множества цветов на конечных точках грани, то существует подсимплекс со сбалансированной разметкой – разметкой, в которой соответствующий гиперграф допускает совершенное дробное паросочетание . Для иллюстрации приведем несколько примеров сбалансированной маркировки для $n = 2$ :

$({1}, {2}, {3})$ — сбалансированы весами $(1, 1, 1)$ .
$({1,2}, {2,3}, {3,1})$ — сбалансированы по весам $(1/2, 1/2, 1/2)$ .
$({1,2}, {2,3}, {1})$ — сбалансированы весами $(0, 1, 1)$ .

Это было доказано Шепли в 1973 году. ^{[ 5 ]} Это комбинаторный аналог леммы ККМС .

Политопальные варианты

Предположим, что у нас есть $d$ -мерный многогранник $P$ с $n$ вершинами. $P$ триангулирован, и каждая вершина триангуляции помечена меткой из ${1, \dots, n}.$ Каждая основная вершина $i$ помечена $i$ . Подсимплекс называется полностью помеченным , если он $d$ -мерен и каждая из его $d + 1$ вершин имеет отдельную метку. Если каждая вершина грани $F$ графа $P$ помечена одной из меток на концах $F$ , то существует не менее $n - d$ полностью помеченных симплексов. Некоторые особые случаи:

$д знак равно п - 1$ . В этом случае $P$ является симплексом. Политопальная лемма Спернера гарантирует, что существует хотя бы один полностью помеченный симплекс. То есть оно сводится к лемме Спернера.
$д = 2$ . Предположим, что двумерный многоугольник с $n$ вершинами триангулирован и помечен метками $1, \dots, n$ так, что на каждой грани между вершиной $i$ и вершиной $i + 1 (mod n)$ только метки $i$ и $i + 1.$ используются . Тогда существует не менее $n - 2$ подтреугольников, в которых используются три разные метки.

Общее утверждение было высказано Атанасовым в 1996 году, который доказал его для случая $d = 2$ . ^{[ 6 ]} Доказательство общего случая было впервые дано де Лоэрой, Петерсоном и Су в 2002 году. ^{[ 7 ]} Они предоставляют два доказательства: первое неконструктивно и использует понятие множеств камешков ; второй конструктивен и основан на аргументах следования путей в графах .

Менье ^{[ 8 ]} распространил теорему с многогранников на многогранные тела, которые не обязательно должны быть выпуклыми или односвязными. В частности, если $P$ — многогранник, то множество его граней является многогранным телом. В каждой разметке Спернера многогранного тела с вершинами $v 1, \dots, v n$ существует по крайней мере:

n-d-1+\left\lceil {\frac {\min _{i=1}^{n}\deg _{B(P)}(v_{i})}{d}}\right\rceil

полностью помеченные симплексы, так что любая пара этих симплексов получает две разные метки. Степень $deg B (P) (vi B)$ — это количество ребер $(P),$ принадлежит $vi которым$ . Поскольку степень не меньше $d$ , нижняя граница не меньше $n - d$ . Но оно может быть больше. Например, для циклического многогранника четырехмерного $с n$ вершинами нижняя граница равна:

n-4-1+\left\lceil {\frac {n-1}{4}}\right\rceil \approx {\frac {5}{4}}n.

Мусин ^{[ 9 ]} далее распространил теорему на $d$ -мерные кусочно-линейные многообразия с краем или без него.

Asada, Frick, Pisharody, Polevy, Stoner, Tsang and Wellner ^{[ 10 ]} далее распространил теорему на псевдомногообразия с краем и улучшил нижнюю оценку количества фасетов с попарно различными метками.

Кубические варианты

Предположим, что вместо симплекса, триангулированного на подсимплексы, мы имеем $n$ -мерный куб, разбитый на более мелкие $n$ -мерные кубы.

Гарольд В. Кун ^{[ 11 ]} доказал следующую лемму. Предположим, куб $[0, M] н$ , для некоторого целого числа $M$ , разбивается на $M н$ единичные кубики. Предположим, что каждая вершина разбиения помечена меткой из ${1, \dots, n + 1},$ так что для каждой вершины $v$ : (1) если $v i = 0$ , то метка на $v$ не превосходит $i$ ; (2) если $v i = M$ , то метка на $v$ не равна $i$ . Тогда существует единичный куб со всеми метками ${1, \dots, n + 1}$ (некоторые из них более одного раза). Особый случай $n = 2$ : предположим, что квадрат разделен на подквадраты, и каждая вершина помечена меткой из ${1,2,3}.$ Левый край помечен цифрой $1$ (= не более 1); нижний край помечен цифрами $1$ или $2$ (= не более 2); верхний край помечен цифрой $1$ или $3$ (= не 2); а правый край помечен цифрой $2$ или $3$ (= не 1). Затем есть квадрат с надписью $1,2,3.$

Другой вариант, связанный с теоремой Пуанкаре – Миранды , ^{[ 12 ]} заключается в следующем. Предположим, куб $[0, M] н$ разделен на $M н$ единичные кубики. Предположим, что каждая вершина помечена двоичным вектором длины $n$ , так что для каждой вершины $v$ : (1) если $v i = 0$ , то координата $i$ метки на $v$ равна 0; (2) если $v i = M$ , то координата $i$ метки на $v$ равна 1; (3) если две вершины являются соседями, то их метки отличаются не более чем на одну координату. Тогда существует единичный куб, в котором все $2 н$ этикетки разные. В двух измерениях эту теорему можно сформулировать еще одним способом: ^{[ 13 ]} в любой разметке, удовлетворяющей условиям (1) и (2), существует хотя бы одна ячейка, в которой сумма меток равна 0 [1-мерная ячейка с $метками (1,1)$ и $(-1,-1)$ , или двумерные ячейки со всеми четырьмя разными метками].

Уолси ^{[ 14 ]} усилил эти два результата, доказав, что число полностью помеченных кубов нечетно.

Мусин ^{[ 13 ]} распространил эти результаты на общие четырехугольники .

Варианты радуги

Предположим, что вместо одной разметки у нас есть $n$ различных разметок Спернера. Мы рассматриваем пары (симплекс, перестановка) такие, что метка каждой вершины симплекса выбирается из разных меток (таким образом, для каждого симплекса существует $n!$ разных пар). Тогда существует по крайней мере $n!$ полностью меченые пары. Это доказал Равиндра Бапат. ^{[ 15 ]} для любой триангуляции. Более простое доказательство, которое работает только для определенных триангуляций, было представлено позже Су. ^{[ 16 ]}

Другой способ сформулировать эту лемму состоит в следующем. Предположим, есть $n$ человек, каждый из которых производит разные разметки Спернера для одной и той же триангуляции. Тогда существует симплекс и такое сопоставление людей с его вершинами, что каждая вершина помечается ее владельцем по-разному (один человек помечает свою вершину цифрой 1, другой человек обозначает ее вершину цифрой 2 и т. д.). Более того, их как минимум $n!$ такие совпадения. С его помощью можно найти вырезку торта, состоящую из соединенных частей, без зависти .

Asada, Frick, Pisharody, Polevy, Stoner, Tsang and Wellner ^{[ 10 ]} распространил эту теорему на псевдомногообразия с краем.

В более общем смысле, предположим, что у нас есть $m$ различных разметок Спернера, где $m$ может отличаться от $n$ . Затем: ^{[ 17 ]}^{: Проблема 2.1}

Для любых натуральных чисел $k 1, \dots, k m ,$ сумма которых равна $m + n - 1$ , существует бэби-симплекс, на котором для каждого $i \in {1, \dots, m}$ номер маркировки $i$ использует не менее $k i$ ( из $n$ ) различных меток. При этом каждая метка используется хотя бы одной (из $m$ ) меткой.
Для любых натуральных чисел $I 1, \dots, I m ,$ сумма которых равна $m + n - 1$ , существует бэби-симплекс, на котором для каждого $j \in {1, \dots, n},$ , метка $j$ используется по крайней мере $l j$ (из $m$ ) разные обозначения.

Обе версии сводятся к лемме Спернера, когда $m = 1$ или когда все $m$ разметки идентичны.

Видеть ^{[ 18 ]} для подобных обобщений.

Ориентированные варианты

Последовательность	Степень
123	1 (один переключатель 1-2 и отсутствие переключателя 2-1)
12321	0 (один переключатель 1-2 минус один переключатель 2-1)
1232	0 (как указано выше; последовательность вызова циклическая)
1231231	2 (два переключателя 1-2 и отсутствие переключателя 2-1)

Браун и Кэрнс ^{[ 19 ]} усилил лемму Спернера, рассмотрев ориентацию симплексов. Каждый субсимплекс имеет ориентацию, которая может быть либо +1, либо -1 (если он полностью помечен), либо 0 (если он не полностью помечен). Они доказали, что сумма всех ориентаций симплексов равна +1. В частности, это означает, что существует нечетное число полностью помеченных симплексов.

В качестве примера для $n = 3$ предположим, что треугольник триангулирован и помечен ${1,2,3}.$ Рассмотрим циклическую последовательность меток на границе треугольника. Определите степень маркировки как количество переключателей от 1 до 2 минус количество переключателей от 2 до 1. См. примеры в таблице справа. Обратите внимание, что степень будет той же самой, если мы будем считать переключения от 2 к 3 минус 3 к 2 или от 3 к 1 минус 1 к 3.

Мусин доказал, что число полностью размеченных треугольников не меньше степени разметки . ^{[ 20 ]} В частности, если степень не равна нулю, то существует хотя бы один полностью помеченный треугольник.

Если разметка удовлетворяет условию Спернера, то ее степень равна ровно 1: переключатели 1-2 и 2-1 имеются только на стороне между вершинами 1 и 2, причем число переключателей 1-2 должно быть на единицу больше числа из 2-1 переключателей (при переходе от вершины 1 к вершине 2). Поэтому исходная лемма Спернера следует из теоремы Мусина.

Деревья и циклы

Аналогичная лемма существует и о конечных и бесконечных деревьях и циклах . ^{[ 21 ]}

Связанные результаты

Мирзахани и Вондрак ^{[ 22 ]} изучите более слабый вариант разметки Спернера, в котором единственным требованием является то, чтобы метка i не использовалась на грани, противоположной вершине i . Они называют это допустимой по Спернеру разметкой . Они показывают, что существуют допустимые по Спернеру разметки, в которых каждая ячейка содержит не более четырех меток. Они также доказывают оптимальную нижнюю границу числа ячеек, которые должны иметь по крайней мере две разные метки в каждой допустимой по Спернеру разметке. Они также доказывают, что для любого допустимого по Спернеру разбиения регулярного симплекса общая площадь границы между частями минимизируется разбиением Вороного .

Приложения

Раскраски Спернера использовались для эффективного вычисления фиксированных точек . Раскраску Спернера можно построить так, чтобы полностью помеченные симплексы соответствовали неподвижным точкам данной функции. Делая триангуляцию все меньше и меньше, можно показать, что пределом полностью помеченных симплексов является именно фиксированная точка. Следовательно, этот метод обеспечивает способ аппроксимации фиксированных точек. Связанное с этим приложение — численное обнаружение периодических орбит и символической динамики . ^{[ 23 ]} Лемму Спернера также можно использовать в алгоритмах поиска корней и справедливого деления алгоритмах ; см. протоколы Симмонса-Су .

Лемма Спернера является одним из ключевых ингредиентов доказательства теоремы Монски о том, что квадрат нельзя разрезать на нечетное число треугольников равной площади . ^{[ 24 ]}

Лемму Спернера можно использовать для нахождения конкурентного равновесия в экономике обмена , хотя существуют более эффективные способы его нахождения. ^{[ 25 ]}^: 67

Спустя пятьдесят лет после первой публикации Спернер представил обзор развития, влияния и применения своей комбинаторной леммы. ^{[ 26 ]}

Эквивалентные результаты

Существует несколько теорем о неподвижной точке, которые представлены в трех эквивалентных вариантах: варианте алгебраической топологии , комбинаторном варианте и варианте покрытия множеств. Каждый вариант можно доказать отдельно, используя совершенно разные аргументы, но каждый вариант можно свести и к другим вариантам в своем ряду. Кроме того, каждый результат верхнюю строку можно вывести из нижней в том же столбце. ^{[ 27 ]}

Алгебраическая топология	Комбинаторика	Комплект покрытия
Теорема Брауэра о неподвижной точке	тема Спернера	Лемма Кнастера – Куратовского – Мазуркевича.
Теорема Борсука – Улама	Лемма Такера	Теорема Люстерника – Шнирельмана

См. также

Топологическая комбинаторика

Ссылки

^ Флегг, Х. Грэм (1974). От геометрии к топологии . Лондон: Издательство английского университета. стр. 84–89. ISBN 0-340-05324-0 .
^ Анатолий (21 мая 2010 г.). «Лемма Спернера» . Блог математических страниц . Проверено 20 июля 2024 г.
^ МакЛеннан, Эндрю; Турки, Раби (2008). «Использование объема для доказательства леммы Спернера» . Экономическая теория . 35 (3): 593–597. дои : 10.1007/s00199-007-0257-0 . ISSN 0938-2259 . JSTOR 40282878 .
^ Чен, Си; Дэн, Сяоте (17 октября 2009 г.). «О сложности двумерной дискретной задачи с фиксированной точкой» . Теоретическая информатика . Автоматы, языки и программирование (ICALP 2006). 410 (44): 4448–4456. дои : 10.1016/j.tcs.2009.07.052 . ISSN 0304-3975 . S2CID 2831759 .
^ Шепли, LS (1973-01-01), Ху, TC ; Робинсон, Стивен М. (ред.), «О сбалансированных играх без побочных платежей» , Математическое программирование , Academic Press, стр. 261–290, ISBN 978-0-12-358350-5 , получено 29 июня 2020 г.
^ Атанасов, К.Т. (1996), «О лемме Спернера», Венгерские исследования математических наук , 32 (1–2): 71–74, MR 1405126
^ Де Лоэра, Хесус А .; Петерсон, Элиша; Су, Фрэнсис Эдвард (2002), «Многогранное обобщение леммы Спернера» , Журнал комбинаторной теории , серия A, 100 (1): 1–26, doi : 10.1006/jcta.2002.3274 , MR 1932067
^ Менье, Фредерик (1 октября 2006 г.). «Разметка Спернера: комбинаторный подход» . Журнал комбинаторной теории . Серия А. 113 (7): 1462–1475. дои : 10.1016/j.jcta.2006.01.006 . ISSN 0097-3165 .
^ Мусин, Олег Р. (01 мая 2015 г.). «Расширения леммы Спернера и Такера для многообразий» . Журнал комбинаторной теории . Серия А. 132 : 172–187. arXiv : 1212.1899 . дои : 10.1016/j.jcta.2014.12.001 . ISSN 0097-3165 . S2CID 5699192 .
^ Jump up to: ^а ^б Асада, Мегуми; Фрик, Флориан; Пишароди, Вивек; Полевой, Максвелл; Стоунер, Дэвид; Цанг, Лин Хэй; Веллнер, Зои (01 января 2018 г.). «Справедливое деление и обобщения результатов типа Спернера и ККМ» . SIAM Journal по дискретной математике . 32 (1): 591–610. arXiv : 1701.04955 . дои : 10.1137/17M1116210 . ISSN 0895-4801 . S2CID 43932757 .
^ Кун, HW (1960), «Некоторые комбинаторные леммы в топологии», IBM Journal of Research and Development , 4 (5): 518–524, doi : 10.1147/rd.45.0518
^ Михаэль Мюгер (2016), Топология для работающего математика (PDF) , Черновик
^ Jump up to: ^а ^б Мусин, Олег Р. (2015), «Лемма типа Спернера для четырехугольников», Московский журнал комбинаторики и теории чисел , 5 (1–2): 26–35, arXiv : 1406.5082 , MR 3476207
^ Уолси, Лоуренс А. (1 июля 1977 г.). «Кубические леммы Спернера как приложения обобщенного дополнительного поворота» . Журнал комбинаторной теории . Серия А. 23 (1): 78–87. дои : 10.1016/0097-3165(77)90081-4 . ISSN 0097-3165 .
^ Бапат, РБ (1989). «Конструктивное доказательство обобщения леммы Спернера, основанного на перестановках». Математическое программирование . 44 (1–3): 113–120. дои : 10.1007/BF01587081 . S2CID 5325605 .
^ Су, Ф.Е. (1999). «Гармония ренты: лемма Спернера о справедливом разделе» . Американский математический ежемесячник . 106 (10): 930–942. дои : 10.2307/2589747 . JSTOR 2589747 .
^ Менье, Фредерик; Су, Фрэнсис Эдвард (2019). «Многозначные версии лемм и приложений Спернера и Фана». SIAM Journal по прикладной алгебре и геометрии . 3 (3): 391–411. arXiv : 1801.02044 . дои : 10.1137/18M1192548 . S2CID 3762597 .
^ Асада, Мегуми; Фрик, Флориан; Пишароди, Вивек; Полевой, Максвелл; Стоунер, Дэвид; Цанг, Лин Хэй; Веллнер, Зоя (2018). «SIAM (Общество промышленной и прикладной математики)». SIAM Journal по дискретной математике . 32 : 591–610. arXiv : 1701.04955 . дои : 10.1137/17m1116210 . S2CID 43932757 .
^ Браун, AB; Кэрнс, СС (1 января 1961 г.). «Усиление леммы Спернера применительно к теории гомологии» . Труды Национальной академии наук . 47 (1): 113–114. Бибкод : 1961ПНАС...47..113Б . дои : 10.1073/pnas.47.1.113 . ISSN 0027-8424 . ПМЦ 285253 . ПМИД 16590803 .
^ Олег Р Мусин (2014). «Вокруг леммы Спернера». arXiv : 1405.7513 [ math.CO ].
^ Нидермайер, Эндрю; Риццоло, Дуглас; Су, Фрэнсис Эдвард (2014), «Лемма Спернера о дереве», в Барге, Александре; Мусин, Олег Р. (ред.), Дискретная геометрия и алгебраическая комбинаторика , Современная математика, том. 625, Провиденс, Род-Айленд: Американское математическое общество, стр. 625-625. 77–92, arXiv : 0909.0339 , doi : 10.1090/conm/625/12492 , ISBN 9781470409050 , МР 3289406 , S2CID 115157240
^ Мирзахани, Марьям; Вондрак, Ян (2017), Лебл, Мартин; Нештирил, Ярослав; Томас, Робин (ред.), «Раскраски Спернера и оптимальное разбиение симплекса» , Путешествие по дискретной математике: дань уважения Иржи Матушеку , Чам: Springer International Publishing, стр. 615–631, arXiv : 1611.08339 , doi : 10.1007/978-3-319-44479-6_25 , ISBN 978-3-319-44479-6 , S2CID 38668858 , получено 25 апреля 2022 г.
^ Гидея, Мариан; Шмало, Ицхак (2018). «Комбинаторный подход к обнаружению неподвижных точек, периодических орбит и символической динамики» . Дискретные и непрерывные динамические системы - А. 38 (12). Американский институт математических наук (AIMS): 6123–6148. arXiv : 1706.08960 . дои : 10.3934/dcds.2018264 . ISSN 1553-5231 . S2CID 119130905 .
^ Айгнер, Мартин ; Циглер, Гюнтер М. (2010), «Один квадрат и нечетное количество треугольников», Доказательства из книги (4-е изд.), Берлин: Springer-Verlag, стр. 131–138, doi : 10.1007/978-3- 642-00856-6_20 , ISBN 978-3-642-00855-9
^ Шарф, Герберт (1967). «Суть игры для N человек». Эконометрика . 35 (1): 50–69. дои : 10.2307/1909383 . JSTOR 1909383 .
^ Спернер, Эмануэль (1980), «Пятьдесят лет дальнейшего развития комбинаторной леммы», Численное решение сильно нелинейных задач (Sympos. Алгоритмы фиксированной точки и проблемы дополнительности, Университет Саутгемптона, Саутгемптон, 1979) , Северная Голландия, Амстердам- Нью-Йорк, стр. 183–197, 199–217, MR. 0559121
^ Найман, Кэтрин Л.; Су, Фрэнсис Эдвард (2013), «Эквивалент Борсука-Улама, который непосредственно подразумевает лемму Спернера» , The American Mathematical Monthly , 120 (4): 346–354, doi : 10.4169/amer.math.monthly.120.04.346 , JSTOR 10.4169/amer.math.monthly.120.04.346 , МР 3035127

Внешние ссылки

Доказательство леммы Спернера при развязывании узла
Лемма Спернера и игра треугольников на n-богатом сайте.
Лемма Спернера в 2D , веб-игра на itch.io.

[1] Флегг, Х. Грэм (1974). От геометрии к топологии . Лондон: Издательство английского университета. стр. 84–89. ISBN 0-340-05324-0 .

[2] Анатолий (21 мая 2010 г.). «Лемма Спернера» . Блог математических страниц . Проверено 20 июля 2024 г.

[3] МакЛеннан, Эндрю; Турки, Раби (2008). «Использование объема для доказательства леммы Спернера» . Экономическая теория . 35 (3): 593–597. дои : 10.1007/s00199-007-0257-0 . ISSN 0938-2259 . JSTOR 40282878 .

[4] Чен, Си; Дэн, Сяоте (17 октября 2009 г.). «О сложности двумерной дискретной задачи с фиксированной точкой» . Теоретическая информатика . Автоматы, языки и программирование (ICALP 2006). 410 (44): 4448–4456. дои : 10.1016/j.tcs.2009.07.052 . ISSN 0304-3975 . S2CID 2831759 .

[5] Шепли, LS (1973-01-01), Ху, TC ; Робинсон, Стивен М. (ред.), «О сбалансированных играх без побочных платежей» , Математическое программирование , Academic Press, стр. 261–290, ISBN 978-0-12-358350-5 , получено 29 июня 2020 г.

[6] Атанасов, К.Т. (1996), «О лемме Спернера», Венгерские исследования математических наук , 32 (1–2): 71–74, MR 1405126

[7] Де Лоэра, Хесус А .; Петерсон, Элиша; Су, Фрэнсис Эдвард (2002), «Многогранное обобщение леммы Спернера» , Журнал комбинаторной теории , серия A, 100 (1): 1–26, doi : 10.1006/jcta.2002.3274 , MR 1932067

[8] Менье, Фредерик (1 октября 2006 г.). «Разметка Спернера: комбинаторный подход» . Журнал комбинаторной теории . Серия А. 113 (7): 1462–1475. дои : 10.1016/j.jcta.2006.01.006 . ISSN 0097-3165 .

[9] Мусин, Олег Р. (01 мая 2015 г.). «Расширения леммы Спернера и Такера для многообразий» . Журнал комбинаторной теории . Серия А. 132 : 172–187. arXiv : 1212.1899 . дои : 10.1016/j.jcta.2014.12.001 . ISSN 0097-3165 . S2CID 5699192 .

[:0-10] Jump up to: ^а ^б Асада, Мегуми; Фрик, Флориан; Пишароди, Вивек; Полевой, Максвелл; Стоунер, Дэвид; Цанг, Лин Хэй; Веллнер, Зои (01 января 2018 г.). «Справедливое деление и обобщения результатов типа Спернера и ККМ» . SIAM Journal по дискретной математике . 32 (1): 591–610. arXiv : 1701.04955 . дои : 10.1137/17M1116210 . ISSN 0895-4801 . S2CID 43932757 .

[k60-11] Кун, HW (1960), «Некоторые комбинаторные леммы в топологии», IBM Journal of Research and Development , 4 (5): 518–524, doi : 10.1147/rd.45.0518

[m15-12] Михаэль Мюгер (2016), Топология для работающего математика (PDF) , Черновик

[:1-13] Jump up to: ^а ^б Мусин, Олег Р. (2015), «Лемма типа Спернера для четырехугольников», Московский журнал комбинаторики и теории чисел , 5 (1–2): 26–35, arXiv : 1406.5082 , MR 3476207

[14] Уолси, Лоуренс А. (1 июля 1977 г.). «Кубические леммы Спернера как приложения обобщенного дополнительного поворота» . Журнал комбинаторной теории . Серия А. 23 (1): 78–87. дои : 10.1016/0097-3165(77)90081-4 . ISSN 0097-3165 .

[b87-15] Бапат, РБ (1989). «Конструктивное доказательство обобщения леммы Спернера, основанного на перестановках». Математическое программирование . 44 (1–3): 113–120. дои : 10.1007/BF01587081 . S2CID 5325605 .

[su1999-16] Су, Ф.Е. (1999). «Гармония ренты: лемма Спернера о справедливом разделе» . Американский математический ежемесячник . 106 (10): 930–942. дои : 10.2307/2589747 . JSTOR 2589747 .

[17] Менье, Фредерик; Су, Фрэнсис Эдвард (2019). «Многозначные версии лемм и приложений Спернера и Фана». SIAM Journal по прикладной алгебре и геометрии . 3 (3): 391–411. arXiv : 1801.02044 . дои : 10.1137/18M1192548 . S2CID 3762597 .

[18] Асада, Мегуми; Фрик, Флориан; Пишароди, Вивек; Полевой, Максвелл; Стоунер, Дэвид; Цанг, Лин Хэй; Веллнер, Зоя (2018). «SIAM (Общество промышленной и прикладной математики)». SIAM Journal по дискретной математике . 32 : 591–610. arXiv : 1701.04955 . дои : 10.1137/17m1116210 . S2CID 43932757 .

[19] Браун, AB; Кэрнс, СС (1 января 1961 г.). «Усиление леммы Спернера применительно к теории гомологии» . Труды Национальной академии наук . 47 (1): 113–114. Бибкод : 1961ПНАС...47..113Б . дои : 10.1073/pnas.47.1.113 . ISSN 0027-8424 . ПМЦ 285253 . ПМИД 16590803 .

[m14-20] Олег Р Мусин (2014). «Вокруг леммы Спернера». arXiv : 1405.7513 [ math.CO ].

[21] Нидермайер, Эндрю; Риццоло, Дуглас; Су, Фрэнсис Эдвард (2014), «Лемма Спернера о дереве», в Барге, Александре; Мусин, Олег Р. (ред.), Дискретная геометрия и алгебраическая комбинаторика , Современная математика, том. 625, Провиденс, Род-Айленд: Американское математическое общество, стр. 625-625. 77–92, arXiv : 0909.0339 , doi : 10.1090/conm/625/12492 , ISBN 9781470409050 , МР 3289406 , S2CID 115157240

[22] Мирзахани, Марьям; Вондрак, Ян (2017), Лебл, Мартин; Нештирил, Ярослав; Томас, Робин (ред.), «Раскраски Спернера и оптимальное разбиение симплекса» , Путешествие по дискретной математике: дань уважения Иржи Матушеку , Чам: Springer International Publishing, стр. 615–631, arXiv : 1611.08339 , doi : 10.1007/978-3-319-44479-6_25 , ISBN 978-3-319-44479-6 , S2CID 38668858 , получено 25 апреля 2022 г.

[23] Гидея, Мариан; Шмало, Ицхак (2018). «Комбинаторный подход к обнаружению неподвижных точек, периодических орбит и символической динамики» . Дискретные и непрерывные динамические системы - А. 38 (12). Американский институт математических наук (AIMS): 6123–6148. arXiv : 1706.08960 . дои : 10.3934/dcds.2018264 . ISSN 1553-5231 . S2CID 119130905 .

[24] Айгнер, Мартин ; Циглер, Гюнтер М. (2010), «Один квадрат и нечетное количество треугольников», Доказательства из книги (4-е изд.), Берлин: Springer-Verlag, стр. 131–138, doi : 10.1007/978-3- 642-00856-6_20 , ISBN 978-3-642-00855-9

[25] Шарф, Герберт (1967). «Суть игры для N человек». Эконометрика . 35 (1): 50–69. дои : 10.2307/1909383 . JSTOR 1909383 .

[26] Спернер, Эмануэль (1980), «Пятьдесят лет дальнейшего развития комбинаторной леммы», Численное решение сильно нелинейных задач (Sympos. Алгоритмы фиксированной точки и проблемы дополнительности, Университет Саутгемптона, Саутгемптон, 1979) , Северная Голландия, Амстердам- Нью-Йорк, стр. 183–197, 199–217, MR. 0559121

[27] Найман, Кэтрин Л.; Су, Фрэнсис Эдвард (2013), «Эквивалент Борсука-Улама, который непосредственно подразумевает лемму Спернера» , The American Mathematical Monthly , 120 (4): 346–354, doi : 10.4169/amer.math.monthly.120.04.346 , JSTOR 10.4169/amer.math.monthly.120.04.346 , МР 3035127

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]

[ 24 ]

[ 25 ]

[ 26 ]

[ 27 ]