Курносый дисфеноид

Курносый дисфеноид
Тип	Дельтаэдр Джонсон Я 83 – Я 84 – Я 85
Лица	12 треугольников
Края	18
Вершины	8
Конфигурация вершин	$4\times (3^{4})+4\times (3^{5})$
Группа симметрии	$D_{2\mathrm {d} }$
Двойной многогранник	Удлиненный гиробифастигий
Характеристики	выпуклый
Сеть

В геометрии курносый дисфеноид представляет собой выпуклый многогранник 12 равносторонних треугольников которого являются , гранями . Это пример дельтаэдра и тела Джонсона . Его можно построить разными способами. Эта форма также имеет альтернативные названия: сиамский додекаэдр , треугольный додекаэдр , тригональный додекаэдр или додекадельтаэдр ; эти названия означают 12-гранный многогранник.

Применение курносого дисфеноида можно визуализировать как кластер атомов, окружающий центральный атом, то есть додекаэдрическую молекулярную геометрию . Его вершины можно поместить в сферу, а также использовать как минимально возможный потенциал Леннарда-Джонса среди всех восьмисферных кластеров. Двойной многогранник курносого дисфеноида представляет собой удлиненный гиробифастигий .

Строительство

Вовлекающий многогранник

Курносый дисфеноид может быть построен по-разному. Как следует из названия, курносый дисфеноид состоит из четырехугольного дисфеноида путем обрезки всех краев его граней и добавления равносторонних треугольников (голубые цвета на следующем изображении), которые скручены под определенным углом между ними. Этот процесс построения известен как курносение .

Процесс построения курносого дисфеноида путем курносения

Курносый дисфеноид также можно построить из треугольной бипирамиды, обрезав два ее края по вершинам. Эти вершины можно сдвинуть друг к другу, в результате чего две новые вершины отодвинутся. В качестве альтернативы, курносый дисфеноид можно построить из пятиугольной бипирамиды, разрезав два края вдоль линии, соединяющей основание бипирамиды, а затем вставив между ними два равносторонних треугольника. Другой способ построения курносого дисфеноида начинается с квадратной антипризмы , заменяя две квадратные грани парами равносторонних треугольников. Другая конструкция курносого дисфеноида представляет собой двуугольный гиробиантикупол . Он имеет ту же топологию и симметрию, но без равносторонних треугольников. Он имеет 4 вершины в квадрате в центральной плоскости в виде двух антикуполов , соединенных с вращательной симметрией.

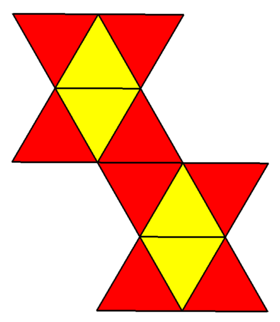
Физическую модель курносого дисфеноида можно сформировать, сложив сетку , состоящую из 12 равносторонних треугольников ( 12-ромбов ), как показано на рисунке. Альтернативная сеть, предложенная Джоном Монтроллом, имеет меньше вогнутых вершин на границе, что делает ее более удобной для оригами . построения

По декартовым координатам

Тогда восьми вершинам курносого дисфеноида можно присвоить декартовы координаты : $${\begin{aligned}(\pm t,r,0),&\qquad (0,-r,\pm t),\\(\pm 1,-s,0),&\qquad (0,s,\pm 1).\end{aligned}}$$Здесь, $q\approx 0.16902$ является положительным действительным решением кубического многочлена ${\textstyle 2x^{3}+11x^{2}+4x-1.}$. Три переменные $r$, $s$, и $t$ является выражением: $$r={\sqrt {q}}\approx 0.41112,\qquad s={\sqrt {\frac {1-q}{2q}}}\approx 1.56786,\qquad t=2rs={\sqrt {2-2q}}\approx 1.28917.$$Поскольку эта конструкция предполагает решение кубического уравнения, курносый дисфеноид нельзя построить с помощью циркуля и линейки , в отличие от других семи дельтаэдров.

Характеристики

В результате таких построений курносый дисфеноид имеет 12 равносторонних треугольников. Дельтаэдр – это многогранник , у которого все грани представляют собой равносторонние треугольники. Имеется восемь выпуклых дельтаэдров, один из которых — курносый дисфеноид. В более общем смысле, выпуклый многогранник, в котором все грани являются правильными многоугольниками, — это тела Джонсона , а каждый выпуклый дельтаэдр — тело Джонсона. Среди них курносый дисфеноид, обозначаемый как 84-е твердое тело Джонсона. $J_{84}$.

Измерение

Курносый дисфеноид с длиной края $a$ имеет площадь поверхности: $$A=3{\sqrt {3}}a^{2}\approx 5.19615a^{2},$$площадь 12 равносторонних треугольников. Его объем можно рассчитать по формуле: $$V\approx 0.85949a^{3}.$$

Симметрия и геодезия

3D-модель курносого дисфеноида

Курносый дисфеноид имеет ту же симметрию, что и тетрагональный дисфеноид , антипризматическая симметрия. $D_{2\mathrm {d} }$ порядка 8: он имеет ось вращательной симметрии 180 °, проходящую через середины двух противоположных краев, две перпендикулярные плоскости отражательной симметрии, проходящие через эту ось, и четыре дополнительные операции симметрии, задаваемые отражением, перпендикулярным оси, за которым следует четверть- поворот и, возможно, еще одно отражение, параллельное оси. .

С точностью до симметрии и параллельного перевода курносый дисфеноид имеет пять типов простых (несамопересекающихся) замкнутых геодезических . Это пути на поверхности многогранника, которые обходят вершины и локально выглядят как кратчайший путь: они следуют по отрезкам прямых, пересекающих каждую грань многогранника, которую они пересекают, и, пересекая ребро многогранника, образуют дополнительные углы на поверхности многогранника. два инцидента обращены к краю. Интуитивно можно было бы натянуть резинку вокруг многогранника по этому пути, и он остался бы на месте: нет возможности локально изменить путь и сделать его короче. Например, один тип геодезической пересекает два противоположных края курносого дисфеноида в их серединах (там, где ось симметрии выходит из многогранника) под углом $\pi /3$. Второй тип геодезической проходит вблизи пересечения курносого дисфеноида с плоскостью, перпендикулярно делящей ось симметрии пополам (экватор многогранника ), пересекая ребра восьми треугольников под углами, чередующимися между $\pi /2$ и $\pi /6$. Смещение геодезической на поверхности многогранника на небольшую величину (достаточно малую, чтобы сдвиг не заставлял ее пересекать какие-либо вершины) сохраняет свойство быть геодезической и сохраняет ее длину, поэтому в обоих этих примерах есть смещенные версии того же типа, которые расположены менее симметрично. Длины пяти простых замкнутых геодезических на курносом дисфеноиде с ребрами единичной длины равны

$2{\sqrt {3}}\approx 3.464$ (для экваториальной геодезической), ${\sqrt {13}}\approx 3.606$, $4$ (для геодезической, проходящей через середины противоположных ребер), $2{\sqrt {7}}\approx 5.292$, и ${\sqrt {19}}\approx 4.359$.

За исключением тетраэдра, который имеет бесконечно много типов простых замкнутых геодезических, курносый дисфеноид имеет наибольшее количество типов геодезических среди всех дельтаэдров.

Представление графом

Курносый дисфеноид является 4-связным , что означает, что для отключения оставшихся вершин требуется удаление четырех вершин. Это один из четырех 4-связных симплициальных хорошо покрытых многогранников, а это означает, что все максимальные независимые множества его вершин имеют одинаковый размер. Остальные три многогранника, обладающие этим свойством, — это правильный октаэдр , пятиугольная бипирамида и неправильный многогранник с 12 вершинами и 20 треугольными гранями.

Двойной многогранник

Двойной многогранник вытянутого гиробифастигия.

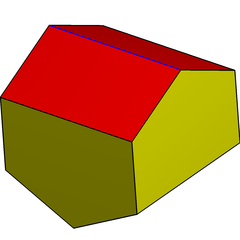
Двойной многогранник курносого дисфеноида представляет собой удлиненный гиробифастигий . Он имеет прямоугольные пятиугольники и может мозаику пространства.

Приложения

Сферы с центрами в вершинах курносого дисфеноида образуют кластер, который согласно численным экспериментам имеет минимально возможный потенциал Леннарда-Джонса среди всех восьмисферных кластеров.

В геометрии химических соединений многогранник можно представить как кластер атомов, окружающий центральный атом. Додекаэдрическая молекулярная геометрия описывает кластер, для которого он является курносым дисфеноидом.

История и именование

Эта форма была названа сиамским додекаэдром в статье Ганса Фройденталя и Б.Л. ван дер Вардена (1947), которые впервые описали набор из восьми выпуклых дельтаэдров .

Название додекадельтаэдр было дано той же форме Берналом (1964) , имея в виду тот факт, что это 12-гранный дельтаэдр. Существуют и другие симплициальные додекаэдры , например шестиугольная бипирамида , но это единственный, который можно реализовать с равносторонними гранями. Бернала интересовала форма отверстий, оставленных в неправильных плотноупакованных сферах, поэтому он использовал ограничительное определение дельтаэдров, в котором дельтаэдр — это выпуклый многогранник с треугольными гранями, которые могут быть образованы центрами набора конгруэнтных граней. сферы, касания которых представляют собой ребра многогранников, и такие, что нет места для размещения еще одной сферы внутри клетки, созданной этой системой сфер. Это ограничительное определение не допускает треугольную бипирамиду (которая образует два тетраэдрических отверстия, а не одно отверстие), пятиугольную бипирамиду (поскольку сферы ее вершин взаимопроникают, поэтому она не может возникнуть в упаковках сфер) и икосаэдр (поскольку в ней есть внутреннее пространство для другой сфера). Бернал пишет, что курносый дисфеноид — «очень распространенное явление». координация в иона кальция кристаллографии » . В координационной геометрии его обычно называют тригональным додекаэдром или просто додекаэдром.

Название курносого дисфеноида происходит от , предложенной Норманом Джонсоном классификации твердых тел Джонсона в 1966 году , — выпуклых многогранников, все грани которых правильные. Впервые он существует в ряду многогранников с осевой симметрией, поэтому ему также можно дать название двуугольный гиробиантикупол .

Внешние ссылки

• Вайсштейн, Эрик В. «Крутой дисфеноид» . Математический мир .