Биувеличенная пятиугольная призма

Биувеличенная пятиугольная призма
Тип	Джонсон Я 52 – Я 53 – Я 54
Лица	8 равносторонних треугольников 3 квадрата 2 пятиугольника
Края	23
Вершины	12
Конфигурация вершин	2(4 2 .5) 2(3 4 ) 2x4(3 2 .4.5)
Группа симметрии	С 2 в
Характеристики	выпуклый
Сеть

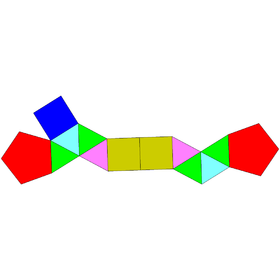В геометрии двуугольная пятиугольная призма представляет собой многогранник, построенный из пятиугольной призмы путем прикрепления двух равносторонних квадратных пирамид к каждой из ее квадратных граней. Это пример твердого Джонсона .

Строительство

Двуугольная пятиугольная призма может быть построена из пятиугольной призмы , прикрепив к каждой из ее квадратных граней две равносторонние квадратные пирамиды - процесс, известный как увеличение . Эти квадратные пирамиды покрывают квадратную грань призмы, поэтому полученный многогранник имеет восемь равносторонних треугольников , три квадрата и два правильных пятиугольника . в качестве граней Выпуклый многогранник , у которого все грани правильные, является телом Джонсона , и в их число входит расширенная пятиугольная призма, обозначаемая как 53-е тело Джонсона. $J_{53}$.

Характеристики

Двуугольная пятиугольная призма с длиной ребра. $a$ имеет площадь поверхности, рассчитанную путем сложения площадей четырех равносторонних треугольников, четырех квадратов и двух правильных пятиугольников: $${\frac {6+4{\sqrt {3}}+{\sqrt {5+2{\sqrt {5}}}}}{2}}a^{2}\approx 9.9051a^{2}.$$Его объем можно получить, разрезав его на правильную пятиугольную призму и равностороннюю квадратную пирамиду, а затем сложив их объем: $${\frac {\sqrt {257+90{\sqrt {5}}+24{\sqrt {50+20{\sqrt {5}}}}}}{12}}a^{3}\approx 2.1919a^{3}.$$

Двугранный угол увеличенной пятиугольной призмы можно рассчитать, сложив двугранный угол равносторонней квадратной пирамиды и правильной пятиугольной призмы:

• двугранный угол увеличенной пятиугольной призмы между двумя соседними треугольными гранями равен углу равносторонней квадратной пирамиды между двумя соседними треугольными гранями, ${\textstyle \arccos \left(-{\frac {1}{3}}\right)\approx 109.5^{\circ }}$,
• двугранный угол увеличенной пятиугольной призмы между двумя соседними квадратными гранями является внутренним углом правильного пятиугольника. ${\textstyle {\frac {3\pi }{5}}=108^{\circ }}$.
• двугранный угол увеличенной пятиугольной призмы между квадратом и пятиугольником равен углу правильной пятиугольной призмы между ее основанием и боковыми гранями ${\textstyle {\frac {\pi }{2}}=90^{\circ }}$.
• двугранный угол увеличенной пятиугольной призмы между пятиугольником и треугольником равен ${\textstyle \arctan \left({\sqrt {2}}\right)+{\frac {\pi }{2}}\approx 144.7^{\circ }}$, для чего сложение двугранного угла равносторонней квадратной пирамиды между ее основанием и боковой гранью ${\textstyle \arctan \left({\sqrt {2}}\right)\approx 54.7^{\circ }}$и двугранный угол правильной пятиугольной призмы между ее основанием и боковой гранью.
• двугранный угол увеличенной пятиугольной призмы между квадратом и треугольником равен ${\textstyle \arctan \left({\sqrt {2}}\right)+{\frac {3\pi }{5}}\approx 162.7^{\circ }}$, для чего складываем двугранный угол равносторонней квадратной пирамиды между ее основанием и боковой гранью и двугранный угол правильной пятиугольной призмы между двумя соседними квадратами.

Внешние ссылки

• Вайсштейн, Эрик В. «Джонсон Солид» . Математический мир .
  • Вайсштейн, Эрик В. «Увеличенная пятиугольная призма» . Математический мир .