Вытянутый квадратный купол

Вытянутый квадратный купол
Вытянутый квадратный купол
Тип	Джонсон ; Я 18 – Я 19 – Я 20
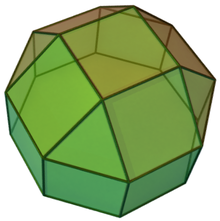
Лица	4 треугольника ; 13 квадратов ; 1 восьмиугольник
Края	36
Вершины	20
Конфигурация вершин	8(4 2 .8) ; 4+8(3.4 3 )
Группа симметрии	С 4В
Двойной многогранник	-
Характеристики	выпуклый
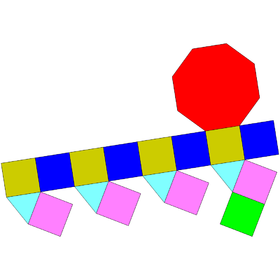
Сеть

В геометрии вытянутый квадратный купол представляет собой многогранник, построенный из восьмиугольной призмы путем прикрепления квадратного купола к ее основанию . Это пример твердого Джонсона .

Строительство

Удлиненный квадратный купол построен из восьмиугольной призмы путем прикрепления квадратного купола к одному из ее оснований - процесс, известный как удлинение . ^[1] Этот купол закрывает грань восьмиугольника так, что образующийся многогранник имеет четыре равносторонних треугольника , тринадцать квадратов и один правильный восьмиугольник . ^[2] многогранник Выпуклый , все грани которого являются правильными многоугольниками, называется телом Джонсона . Вытянутый квадратный купол — один из них, причисленный к девятнадцатому корпусу Джонсона. $J_{19}$ . ^[3]

Тело Джонсона — это один из 92 строго выпуклых многогранников , которые состоят из правильных многоугольных граней, но не являются однородными многогранниками (то есть не являются платоновыми телами , архимедовыми телами , призмами или антипризмами ). Их назвал Норман Джонсон , который впервые перечислил эти многогранники в 1966 году. ^[4]

Характеристики

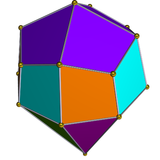
Площадь поверхности вытянутого квадратного купола $A$ представляет собой сумму площадей всех многоугольных граней. Его объем $V$ В этом можно убедиться, расчленив его на квадратный купол и правильный восьмиугольник, а затем сложив их объемы. Учитывая вытянутую треугольную главку с длиной ребра $a$ , его площадь поверхности и объем равны: ^[5] ${\begin{aligned}A&=\left(15+2{\sqrt {2}}+{\sqrt {3}}\right)a^{2}\approx 19.561a^{2},\\V&=\left(3+{\frac {8{\sqrt {2}}}{3}}\right)a^{3}\approx 6.771a^{3}.\end{aligned}}$

Двойной многогранник вытянутой квадратной главки имеет 20 граней: 8 равнобедренных треугольников, 4 коршуна, 8 четырехугольников.

Двойной вытянутый квадратный купол	Чистая двойная

Связанные многогранники и соты

Вытянутый квадратный купол образует заполняющие пространство соты с тетраэдрами и кубами ; с кубами и кубооктаэдрами ; и с тетраэдрами, вытянутыми квадратными пирамидами и вытянутыми квадратными бипирамидами . (Последние две единицы можно разложить на кубы и квадратные пирамиды .) ^[6]

Ссылки

^ Раджваде, А.Р. (2001), Выпуклые многогранники с условиями регулярности и третья проблема Гильберта , Тексты и материалы по математике, Книжное агентство Hindustan, стр. 84–89, номер домена : 10.1007/978-93-86279-06-4 , ISBN. 978-93-86279-06-4 .
^ Берман, Мартин (1971), «Выпуклые многогранники с правильными гранями», Журнал Института Франклина , 291 (5): 329–352, doi : 10.1016/0016-0032(71)90071-8 , MR 0290245 .
^ Фрэнсис, Дэррил (август 2013 г.), «Твердые тела Джонсона и их сокращения» , Word Ways , 46 (3): 177 .
^ Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Canadian Journal of Mathematics , 18 : 169–200, doi : 10.4153/cjm-1966-021-8 , MR 0185507 , Zbl 0132.14603 .
^ Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Canadian Journal of Mathematics , 18 : 169–200, doi : 10.4153/cjm-1966-021-8 , MR 0185507 , S2CID 122006114 , Zbl 0132.14603 .
^ «Соты J19» .

Внешние ссылки

Вайсштейн, Эрик В. , « Удлиненный квадратный купол » (« Тело Джонсона ») в MathWorld .

Эта многогранникам, статья, посвященная незавершена . Вы можете помочь Википедии, расширив ее .

[rajwade-1] Раджваде, А.Р. (2001), Выпуклые многогранники с условиями регулярности и третья проблема Гильберта , Тексты и материалы по математике, Книжное агентство Hindustan, стр. 84–89, номер домена : 10.1007/978-93-86279-06-4 , ISBN. 978-93-86279-06-4 .

[berman-2] Берман, Мартин (1971), «Выпуклые многогранники с правильными гранями», Журнал Института Франклина , 291 (5): 329–352, doi : 10.1016/0016-0032(71)90071-8 , MR 0290245 .

[francis-3] Фрэнсис, Дэррил (август 2013 г.), «Твердые тела Джонсона и их сокращения» , Word Ways , 46 (3): 177 .

[4] Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Canadian Journal of Mathematics , 18 : 169–200, doi : 10.4153/cjm-1966-021-8 , MR 0185507 , Zbl 0132.14603 .

[johnson-5] Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Canadian Journal of Mathematics , 18 : 169–200, doi : 10.4153/cjm-1966-021-8 , MR 0185507 , S2CID 122006114 , Zbl 0132.14603 .

[6] «Соты J19» .

[1]

[2]

[3]

[4]

[5]

[6]

v т и Твердые вещества Джонсона
Пирамиды , купола и круги	квадратная пирамида пятиугольная пирамида треугольный купол квадратный купол пятиугольный купол пятиугольная ротонда
Модифицированные пирамиды	вытянутая треугольная пирамида вытянутая квадратная пирамида вытянутая пятиугольная пирамида Гироудлиненная квадратная пирамида гироудлиненная пятиугольная пирамида треугольная бипирамида пятиугольная бипирамида вытянутая треугольная бипирамида вытянутая квадратная бипирамида вытянутая пятиугольная бипирамида гироудлиненная квадратная бипирамида
Модифицированные купола и раунды	удлиненный треугольный купол вытянутый квадратный купол удлиненный пятиугольный купол вытянутая пятиугольная ротонда гироудлинённый треугольный купол гироудлиненный квадратный купол гироудлиненный пятиугольный купол гироудлиненная пятиугольная ротонда гиробифастигий треугольный ортобикупол квадратный ортобикупол квадратный гиробикупол пятиугольный ортобикупол пятиугольный гирокупол пятиугольная ортокуполаротонда пятиугольная гирокуполаротонда пятиугольная ортобиротонда удлиненный треугольный ортобикупол удлиненный треугольный гиробикупол вытянутый квадратный гиробикупол удлиненный пятиугольный ортобикупол удлиненный пятиугольный гиробикупол вытянутая пятиугольная ортокуполаротонда вытянутая пятиугольная гирокуполаротонда вытянутая пятиугольная ортобиротонда вытянутая пятиугольная гиробиротунда гироудлиненный треугольный двуглавый купол гироудлиненный квадратный двуглавый купол гироудлиненный пятиугольный двуглавый купол гироудлинённый пятиугольный купол-ротонда гироудлиненная пятиугольная биротонда
Дополненные призмы	увеличенная треугольная призма смещенная треугольная призма триаугментированная треугольная призма увеличенная пятиугольная призма увеличенная пятиугольная призма дополненная шестиугольная призма парабиоувеличенная шестиугольная призма метаувеличенная шестиугольная призма трехугольная шестиугольная призма
Модифицированные платоновые тела	дополненный додекаэдр парабиоувеличенный додекаэдр метаувеличенный додекаэдр триаугментированный додекаэдр метабидиминированный икосаэдр трехмерный икосаэдр увеличенный трехмерный икосаэдр
Модифицированные архимедовы тела	расширенный усеченный тетраэдр дополненный усеченный куб увеличенный усеченный куб дополненный усеченный додекаэдр парабиоувеличенный усеченный додекаэдр метаувеличенный усеченный додекаэдр триаугментированный усеченный додекаэдр вращающийся ромбокосододекаэдр парабигиратный ромбикосидодекаэдр метабивративный ромбокосододекаэдр тригиратный ромбикосидодекаэдр уменьшенный ромбокосододекаэдр парагиратный уменьшенный ромбикосидодекаэдр метавращающийся уменьшенный ромбокосододекаэдр большой, уменьшенный ромбокосододекаэдр парабидиуменьшенный ромбокосододекаэдр метабидиминированный ромбикосододекаэдр вращающийся двууменьшенный ромбокосододекаэдр трехмерный ромбикосидодекаэдр
Элементарные твердые тела	курносый дисфеноид курносая квадратная антипризма сфенокорона расширенная сфенокорона сфеномегакорона Гебесфеномегакорона дисфеномен коды неисправностей треугольная гебесфеноротонда
(См. также Список твердых тел Джонсона , сортируемую таблицу)