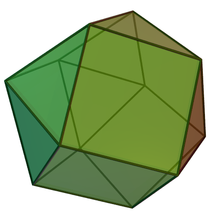
Треугольный ортобикупол

Треугольный ортобикупол
Тип	Джонсон Я 26 – Я 27 – Я 28
Лица	2+6 треугольников 6 квадратов
Края	24
Вершины	12
Конфигурация вершин	6(3 2 .4 2 ) 6(3.4.3.4)
Группа симметрии	Д 3 часа
Двойной многогранник	Трапезо-ромбический додекаэдр
Характеристики	выпуклый
Сеть

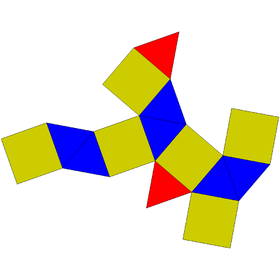В геометрии треугольный ортобикупол является одним из тел Джонсона ( J ₂₇ ). Как следует из названия, его можно построить, прикрепив два треугольных купола ( J ₃ ) вдоль их оснований. В каждой вершине он имеет одинаковое количество квадратов и треугольников; однако он не является вершинно-транзитивным . Его еще называют антикубооктаэдром , скрученным кубооктаэдром или дисептаэдром . Это также канонический многогранник .

Тело Джонсона — это один из 92 строго выпуклых многогранников , которые состоят из правильных многоугольных граней, но не являются однородными многогранниками (то есть не являются платоновыми телами , архимедовыми телами , призмами или антипризмами ). Их назвал Норман Джонсон , который впервые перечислил эти многогранники в 1966 году.

Треугольный ортобикупола — первый в бесконечном множестве ортобикуполов .

Строительство

Треугольный ортобикупол можно построить, прикрепив два треугольных купола к их основаниям . Подобно кубооктаэдру , который будет известен как треугольный гиробикупола , разница состоит в том, что два треугольных купола, составляющие треугольный ортобикупол, соединены так, что пары совпадающих сторон соприкасаются (отсюда и «орто»); кубооктаэдр соединен так, что треугольники примыкают к квадратам, и наоборот. Учитывая треугольный ортобикупол, поворот одного купола на 60 градусов перед соединением дает кубооктаэдр. Следовательно, другое название треугольного ортобикупола — антикубооктаэдр . Поскольку треугольный ортобикупол обладает свойством выпуклости , а его грани представляют собой правильные многоугольники (восемь равносторонних треугольников и шесть квадратов ), его классифицируют как тело Джонсона . Он считается двадцать седьмым твердым телом Джонсона. $J_{27}$

Характеристики

Площадь поверхности $A$ и объем $V$ треугольного ортобикупола такие же, как и у кубооктаэдра. Площадь его поверхности можно получить, суммируя все его многоугольные грани, а объем — разрезав его на два треугольных купола и сложив их объемы. С длиной края $a$, они есть: $${\begin{aligned}A&=2\left(3+{\sqrt {3}}\right)a^{2}\approx 9.464a^{2},\\V&={\frac {5{\sqrt {2}}}{3}}a^{3}\approx 2.357a^{3}.\end{aligned}}$$

Связанные многогранники и соты

Выпрямленные кубические соты можно разобрать и перестроить в виде заполняющей пространство решетки изтреугольные ортобикуполы и квадратные пирамиды .

Двойником треугольного ортобикупола является трапецоромбический додекаэдр . Он имеет 6 ромбических и 6 трапециевидных граней и похож на ромбдодекаэдр .

Внешние ссылки

• Вайсштейн, Эрик В. , « Тело Джонсона » (« Треугольный ортобикупол ») в MathWorld .