| 1 | Равносторонняя квадратная пирамида |  | 5 | 8 | 5 |  порядка 8 порядка 8 |  |
|---|
| 2 | Пятиугольная пирамида |  | 6 | 10 | 6 |  порядка 10 порядка 10 |  |
|---|
| 3 | Треугольный купол |  | 9 | 15 | 8 |  порядка 6 порядка 6 |  |
|---|
| 4 | Квадратный купол |  | 12 | 20 | 10 |  порядка 8 порядка 8 |  |
|---|
| 5 | Пятиугольный купол |  | 15 | 25 | 12 |  порядка 10 порядка 10 |  |
|---|
| 6 | Пятиугольная ротонда |  | 20 | 35 | 17 |  порядка 10 порядка 10 |  |
|---|
| 7 | Вытянутая треугольная пирамида |  | 7 | 12 | 7 |  порядка 6 порядка 6 |  |
|---|
| 8 | Вытянутая квадратная пирамида |  | 9 | 16 | 9 |  порядка 8 порядка 8 |  |
|---|
| 9 | Вытянутая пятиугольная пирамида |  | 11 | 20 | 11 |  порядка 10 порядка 10 |  |
|---|
| 10 | Гироудлиненная квадратная пирамида |  | 9 | 20 | 13 |  порядка 8 порядка 8 |  |
|---|
| 11 | Гироудлиненная пятиугольная пирамида |  | 11 | 25 | 16 |  порядка 10 порядка 10 |  |
|---|
| 12 | Треугольная бипирамида |  | 5 | 9 | 6 |  порядка 12 порядка 12 |  |
|---|
| 13 | Пятиугольная бипирамида |  | 7 | 15 | 10 |  порядка 20 порядка 20 |  |
|---|
| 14 | Вытянутая треугольная бипирамида |  | 8 | 15 | 9 |  порядка 12 порядка 12 |  |
|---|
| 15 | Вытянутая квадратная бипирамида |  | 10 | 20 | 12 |  порядка 16 порядка 16 |  |
|---|
| 16 | Вытянутая пятиугольная бипирамида |  | 12 | 25 | 15 |  порядка 20 порядка 20 |  |
|---|
| 17 | Гироудлиненная квадратная бипирамида |  | 10 | 24 | 16 |  порядка 16 порядка 16 |  |
|---|
| 18 | Вытянутый треугольный купол | 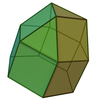 | 15 | 27 | 14 |  порядка 6 порядка 6 |  |
|---|
| 19 | Вытянутый квадратный купол | 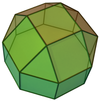 | 20 | 36 | 18 |  порядка 8 порядка 8 |  |
|---|
| 20 | Вытянутый пятиугольный купол |  | 25 | 45 | 22 |  порядка 10 порядка 10 |  |
|---|
| 21 | Вытянутая пятиугольная ротонда |  | 30 | 55 | 27 |  порядка 10 порядка 10 |  |
|---|
| 22 | Гироудлиненный треугольный купол |  | 15 | 33 | 20 |  порядка 6 порядка 6 |  |
|---|
| 23 | Гироудлиненный квадратный купол | 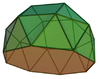 | 20 | 44 | 26 |  порядка 8 порядка 8 |  |
|---|
| 24 | Гироудлиненный пятиугольный купол |  | 25 | 55 | 32 |  порядка 10 порядка 10 |  |
|---|
| 25 | Гироудлиненная пятиугольная ротонда |  | 30 | 65 | 37 |  порядка 10 порядка 10 |  |
|---|
| 26 | Гиробифастигиум |  | 8 | 14 | 8 |  порядка 8 порядка 8 |  |
|---|
| 27 | Треугольный ортобикупол |  | 12 | 24 | 14 |  порядка 12 порядка 12 |  |
|---|
| 28 | Квадратный ортобикупол |  | 16 | 32 | 18 |  порядка 16 порядка 16 |  |
|---|
| 29 | Гиробикупол квадратный |  | 16 | 32 | 18 |  порядка 16 порядка 16 |  |
|---|
| 30 | Пятиугольный ортобикупол |  | 20 | 40 | 22 |  порядка 20 порядка 20 |  |
|---|
| 31 | Пятиугольный гиробикупола |  | 20 | 40 | 22 |  порядка 20 порядка 20 |  |
|---|
| 32 | Пятиугольная ортокуполаротонда |  | 25 | 50 | 27 |  порядка 10 порядка 10 |  |
|---|
| 33 | Пятиугольная гирокуполаротонда |  | 25 | 50 | 27 |  порядка 10 порядка 10 |  |
|---|
| 34 | Пятиугольная ортобиротонда |  | 30 | 60 | 32 |  порядка 20 порядка 20 |  |
|---|
| 35 | Удлиненный треугольный ортобикупол. |  | 18 | 36 | 20 |  порядка 12 порядка 12 |  |
|---|
| 36 | Гиробикупол вытянутой треугольной формы. |  | 18 | 36 | 20 |  порядка 12 порядка 12 |  |
|---|
| 37 | Вытянутый квадратный гиробикупол. |  | 24 | 48 | 26 |  порядка 16 порядка 16 |  |
|---|
| 38 | Удлиненный пятиугольный ортобикупол. |  | 30 | 60 | 32 |  порядка 20 порядка 20 |  |
|---|
| 39 | Удлиненный пятиугольный гиробикупол. |  | 30 | 60 | 32 |  порядка 20 порядка 20 |  |
|---|
| 40 | Вытянутая пятиугольная ортокуполаротонда. |  | 35 | 70 | 37 |  порядка 10 порядка 10 |  |
|---|
| 41 | Вытянутая пятиугольная гирокуполаротонда. |  | 35 | 70 | 37 |  порядка 10 порядка 10 |  |
|---|
| 42 | Вытянутая пятиугольная ортобиротонда. |  | 40 | 80 | 42 |  порядка 20 порядка 20 |  |
|---|
| 43 | Удлинённая пятиугольная гиробиротунда. |  | 40 | 80 | 42 |  порядка 20 порядка 20 |  |
|---|
| 44 | Гироудлинённый треугольный бикупол |  | 18 | 42 | 26 |  порядка 6 порядка 6 |  |
|---|
| 45 | Гироудлиненный квадратный бикупол |  | 24 | 56 | 34 |  порядка 8 порядка 8 |  |
|---|
| 46 | Гироудлиненный пятиугольный бикупол |  | 30 | 70 | 42 |  порядка 10 порядка 10 |  |
|---|
| 47 | Гироудлинённый пятиугольный купол-ротонда |  | 35 | 80 | 47 |  порядка 5 порядка 5 |  |
|---|
| 48 | Гироудлиненная пятиугольная биротонда |  | 40 | 90 | 52 |  порядка 10 порядка 10 |  |
|---|
| 49 | Увеличенная треугольная призма | 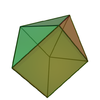 | 7 | 13 | 8 |  порядка 4 порядка 4 |  |
|---|
| 50 | Увеличенная треугольная призма |  | 8 | 17 | 11 |  порядка 4 порядка 4 |  |
|---|
| 51 | Триаугментированная треугольная призма |  | 9 | 21 | 14 |  порядка 12 порядка 12 |  |
|---|
| 52 | Дополненная пятиугольная призма | 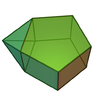 | 11 | 19 | 10 |  порядка 4 порядка 4 |  |
|---|
| 53 | Биувеличенная пятиугольная призма | 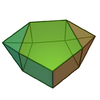 | 12 | 23 | 13 |  порядка 4 порядка 4 |  |
|---|
| 54 | Дополненная шестиугольная призма | 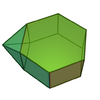 | 13 | 22 | 11 |  порядка 4 порядка 4 |  |
|---|
| 55 | Парабиаугментированная шестиугольная призма | 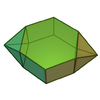 | 14 | 26 | 14 |  порядка 8 порядка 8 |  |
|---|
| 56 | Метабиаувеличенная шестиугольная призма | 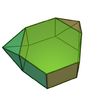 | 14 | 26 | 14 |  порядка 4 порядка 4 |  |
|---|
| 57 | Триаугментированная шестиугольная призма |  | 15 | 30 | 17 |  порядка 12 порядка 12 |  |
|---|
| 58 | Дополненный додекаэдр | 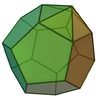 | 21 | 35 | 16 |  порядка 10 порядка 10 |  |
|---|
| 59 | Парабиаугментированный додекаэдр |  | 22 | 40 | 20 |  порядка 20 порядка 20 |  |
|---|
| 60 | Метабиаугментированный додекаэдр |  | 22 | 40 | 20 |  порядка 4 порядка 4 |  |
|---|
| 61 | Триаугментированный додекаэдр | 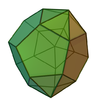 | 23 | 45 | 24 |  порядка 6 порядка 6 |  |
|---|
| 62 | Метабидиминидированный икосаэдр |  | 10 | 20 | 12 |  порядка 4 порядка 4 |  |
|---|
| 63 | Трехмерный икосаэдр |  | 9 | 15 | 8 |  порядка 6 порядка 6 |  |
|---|
| 64 | Увеличенный трехмерный икосаэдр | 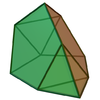 | 10 | 18 | 10 |  порядка 6 порядка 6 |  |
|---|
| 65 | Дополненный усеченный тетраэдр |  | 15 | 27 | 14 |  порядка 6 порядка 6 |  |
|---|
| 66 | Дополненный усеченный куб |  | 28 | 48 | 22 |  порядка 8 порядка 8 |  |
|---|
| 67 | Улучшенный усеченный куб |  | 32 | 60 | 30 |  порядка 16 порядка 16 |  |
|---|
| 68 | Дополненный усеченный додекаэдр | 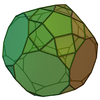 | 65 | 105 | 42 |  порядка 10 порядка 10 |  |
|---|
| 69 | Парабиаугментированный усеченный додекаэдр | 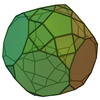 | 70 | 120 | 52 |  порядка 20 порядка 20 |  |
|---|
| 70 | Метабиаугментированный усеченный додекаэдр |  | 70 | 120 | 52 |  порядка 4 порядка 4 |  |
|---|
| 71 | Триаугментированный усеченный додекаэдр |  | 75 | 135 | 62 |  порядка 6 порядка 6 |  |
|---|
| 72 | Вращающийся ромбокосододекаэдр |  | 60 | 120 | 62 |  порядка 10 порядка 10 |  |
|---|
| 73 | Парабигратный ромбокосододекаэдр |  | 60 | 120 | 62 |  порядка 20 порядка 20 |  |
|---|
| 74 | Метабигиратный ромбикосидодекаэдр |  | 60 | 120 | 62 |  порядка 4 порядка 4 |  |
|---|
| 75 | Тригиратный ромбикосидодекаэдр |  | 60 | 120 | 62 |  порядка 6 порядка 6 |  |
|---|
| 76 | Уменьшенный ромбокосододекаэдр |  | 55 | 105 | 52 |  порядка 10 порядка 10 |  |
|---|
| 77 | Парагиратный уменьшенный ромбикосидодекаэдр |  | 55 | 105 | 52 |  порядка 10 порядка 10 |  |
|---|
| 78 | Метагиратный уменьшенный ромбикосододекаэдр |  | 55 | 105 | 52 |  порядка 2 порядка 2 |  |
|---|
| 79 | Бигиратный уменьшенный ромбокосододекаэдр |  | 55 | 105 | 52 |  порядка 2 порядка 2 |  |
|---|
| 80 | Парабидоуменьшенный ромбокосододекаэдр |  | 50 | 90 | 42 |  порядка 20 порядка 20 |  |
|---|
| 81 | Метабидиминированный ромбикосододекаэдр |  | 50 | 90 | 42 |  порядка 4 порядка 4 |  |
|---|
| 82 | Вращающийся двууменьшенный ромбикосидодекаэдр |  | 50 | 90 | 42 |  порядка 2 порядка 2 |  |
|---|
| 83 | Трехмерный ромбокосододекаэдр |  | 45 | 75 | 32 |  порядка 6 порядка 6 |  |
|---|
| 84 | Курносый дисфеноид |  | 8 | 18 | 12 |  порядка 8 порядка 8 |  |
|---|
| 85 | Курносая квадратная антипризма |  | 16 | 40 | 26 |  порядка 16 порядка 16 |  |
|---|
| 86 | Сфенокорона |  | 10 | 22 | 14 |  порядка 4 порядка 4 |  |
|---|
| 87 | Дополненная сфенокорона |  | 11 | 26 | 17 |  порядка 2 порядка 2 |  |
|---|
| 88 | Сфеномегакорона |  | 12 | 28 | 18 |  порядка 4 порядка 4 |  |
|---|
| 89 | Гебесфеномегакорона |  | 14 | 33 | 21 |  порядка 4 порядка 4 |  |
|---|
| 90 | дисфеноцинальный | 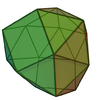 | 16 | 38 | 24 |  порядка 8 порядка 8 |  |
|---|
| 91 | Время отказа |  | 14 | 26 | 14 |  порядка 8 порядка 8 |  |
|---|
| 92 | Треугольная гебесфеноротонда |  | 18 | 36 | 20 |  порядка 6 порядка 6 |  |
|---|





































































































































































































