Вытянутый квадратный гиробикупол.

Вытянутый квадратный гиробикупол.
Вытянутый квадратный гиробикупол.
Тип	Канонический , ; Джонсон ; Я 36 – Я 37 – Я 38
Лица	8 треугольников ; 18 квадратов
Края	48
Вершины	24
Конфигурация вершин
Группа симметрии
Двойной многогранник	Псевдодельтоидный икоситетраэдр
Характеристики	выпуклый , ; единственной вершины фигура
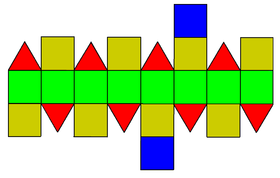
Сеть

В геометрии вытянутый квадратный гиробикупол представляет собой многогранник, построенный из двух квадратных куполов, прикрепленных к основаниям восьмиугольной призмы , при этом один из них повернут. ошибочно считали его ромбокубооктаэдром Когда-то многие математики . Оно не считается архимедовым телом, поскольку в нем отсутствует набор глобальных симметрий , которые сопоставляют каждую вершину с каждой другой вершиной, в отличие от 13 архимедовых тел. Это также канонический многогранник . По этой причине он также известен как псевдоромбокубооктаэдр , твердое тело Миллера , ^[1] или твердое тело Миллера-Аскинузе . ^[2]

Строительство

Удлиненный квадратный гиробикупол можно построить аналогично ромбокубооктаэдру , прикрепив два правильных квадратных купола к основаниям восьмиугольной призмы (процесс, известный как удлинение) . Разница между этими двумя многогранниками заключается в том, что один из двух квадратных куполов вытянутого квадратного гиробикупола скручен на 45 градусов, процесс, известный как вращение , в результате чего треугольные грани смещаются вертикально. ^[3]^[1] Получившийся многогранник имеет 8 равносторонних треугольников и 18 квадратов . ^[3] Выпуклый , среди них — многогранник, у которого все грани являются правильными многоугольниками , — это тело Джонсона вытянутый квадратный гиробикупола, нумерованный как 37-е тело Джонсона. $J_{37}$ . ^[4]

Процесс строительства вытянутого квадратного гиробикупола.

Удлиненный квадратный гиробикупола, возможно, был открыт Иоганном Кеплером при перечислении архимедовых тел, но его первое явное появление в печати, по-видимому, относится к работе Дункана Соммервилля в 1905 году. ^[5] Он был независимо переоткрыт Дж. К. П. Миллером в 1930 году по ошибке при попытке построить модель ромбокубооктаэдра . Это твердое тело было вновь открыто В.Г. Ашкинусе в 1957 году. ^[1]^[6]^[7]

Характеристики

Гиробикупол вытянутой формы квадратной формы с длиной ребра. $a$ имеет площадь поверхности: ^[3] $\left(18+2{\sqrt {3}}\right)a^{2}\approx 21.464a^{2},$ сложив площади 8 равносторонних треугольников и 10 квадратов. Его объем можно вычислить, разрезав его на два квадратных купола и одну восьмиугольную призму: ^[3] ${\frac {12+10{\sqrt {2}}}{3}}a^{3}\approx 8.714a^{3}.$

Вытянутый квадратный гиробикупол обладает трехмерной группой симметрии. $D_{4\mathrm {d} }$ порядка 16. Он локально вершинно-регулярен – расположение четырех граней, инцидентных любой вершине, одинаково для всех вершин; это уникальное явление среди твердых тел Джонсона. Однако способ его «скручивания» дает ему отдельный «экватор» и два отдельных «полюса», что, в свою очередь, делит его вершины на 8 «полярных» вершин (по 4 на каждый полюс) и 16 «экваториальных» вершин. Следовательно, оно не является вершинно-транзитивным и, следовательно, обычно не считается 14-м архимедовым телом . ^[1]^[7]^[8]

Двугранный угол вытянутого квадратного гиробикупола можно определить аналогично ромбокубооктаэдру, сложив двугранный угол квадратного купола и восьмиугольной призмы: ^[2]

двугранный угол ромбокубооктаэдра между двумя соседними квадратами сверху и снизу равен углу квадратного купола 135 °. Двугранный угол восьмиугольной призмы между двумя соседними квадратами равен внутреннему углу правильного восьмиугольника , равному 135°. Двугранный угол между двумя соседними квадратами на ребре, где квадратный купол прикреплен к восьмиугольной призме, есть сумма двугранного угла квадратного купола, соединяющего квадрат с восьмиугольником, и двугранного угла восьмиугольной призмы, соединяющего квадрат с восьмиугольником 45 ° + 90° = 135°. Следовательно, двугранный угол ромбокубооктаэдра для каждых двух соседних квадратов равен 135°.
двугранный угол ромбокубооктаэдра, соединяющего квадрат с треугольником, равен углу квадратного купола между ними и составляет 144,7 °. Двугранный угол между квадратом и треугольником на ребре, где квадратный купол прикреплен к восьмиугольной призме, представляет собой сумму двугранного угла квадратного купола, соединяющего треугольник с восьмиугольником, и двугранного угла восьмиугольной призмы, соединяющей квадрат и восьмиугольник. -восьмиугольник 54,7° + 90° = 144,7°. Следовательно, двугранный угол ромбокубооктаэдра для каждого квадрата к треугольнику равен 144,7 °.

Если лица окрашены в соответствии с симметрией D _4d , это может выглядеть так:

Псевдодельтоидный икоситетраэдр (справа) — это двойственный многогранник .

расположены 8 (зеленых) квадратов Вокруг экватора , 4 (красных) треугольника и 4 (желтых) квадрата сверху и снизу, а также по одному (синему) квадрату на каждом полюсе.

Связанные многогранники и соты

Вытянутый квадратный гиробикупола может образовывать заполняющую пространство соту с правильным тетраэдром , кубом и кубооктаэдром . Он также может образовывать другие соты с тетраэдром, квадратной пирамидой и различными комбинациями кубов, вытянутыми квадратными пирамидами и вытянутыми квадратными бипирамидами . ^[9]

Псевдобольшой ромбокубооктаэдр — невыпуклый аналог псевдоромбокубооктаэдра, построенный аналогичным образом из невыпуклого большого ромбокубооктаэдра .

По химии

- ион Поливанадат [ V ₁₈ O ₄₂ ] ¹²⁻ имеет псевдоромбокубооктаэдрическую структуру, где каждая квадратная грань выступает в качестве основания пирамиды ВО ₅ . ^[10]

Ссылки

^ Jump up to: Перейти обратно: ^а ^б ^с ^д Кромвель, Питер Р. (1997), Многогранники , издательство Кембриджского университета , стр. 91, ISBN 978-0-521-55432-9 .
^ Jump up to: Перейти обратно: ^а ^б Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Canadian Journal of Mathematics , 18 : 169–200, doi : 10.4153/cjm-1966-021-8 , MR 0185507 , S2CID 122006114 , Zbl 0132.14603 .
^ Jump up to: Перейти обратно: ^а ^б ^с ^д Берман, Мартин (1971), «Выпуклые многогранники с правильными гранями», Журнал Института Франклина , 291 (5): 329–352, doi : 10.1016/0016-0032(71)90071-8 , MR 0290245 .
^ Фрэнсис, Дэррил (август 2013 г.), «Твердые тела Джонсона и их сокращения» , Word Ways , 46 (3): 177 .
^ Соммервилль, ДМЙ (1905), «Полурегулярные сети плоскости в абсолютной геометрии» , Труды Королевского общества Эдинбурга , 41 : 725–747, doi : 10.1017/s0080456800035560 . Цитируется Грюнбаумом (2009) .
^ Болл, Роуз (1939), Коксетер, HSM (ред.), Математические воссоздания и эссе (11-е изд.), стр. 137 .
^ Jump up to: Перейти обратно: ^а ^б Грюнбаум, Бранко (2009), «Непреходящая ошибка» (PDF) , Elemente der Mathematik , 64 (3): 89–101, doi : 10.4171/EM/120 , MR 2520469 Перепечатано в Питичи, Мирча, изд. (2011). Лучшее сочинение по математике 2010 года . Издательство Принстонского университета. стр. 18–31. .
^ Ландо, Сергей К.; Звонкин, Александр К. (2004), Графы на поверхностях и их применение , Springer, с. 114, номер домена : 10.1007/978-3-540-38361-1 , ISBN. 978-3-540-38361-1 .
^ «Соты J37» , Галерея деревянных многогранников , получено 21 марта 2016 г.
^ Гринвуд, Норман Н .; Эрншоу, Алан (1997). Химия элементов (2-е изд.). Баттерворт-Хайнеманн . п. 986. ИСБН 978-0-08-037941-8 .

Дальнейшее чтение

Энтони Пью (1976), Многогранники: визуальный подход , Калифорния: Издательство Калифорнийского университета в Беркли, ISBN 0-520-03056-7 Глава 2: Архимедовы многогранники, призмы и антипризмы, с. 25 Псевдоромбокубооктаэдр

Внешние ссылки

[cromwell-1] Jump up to: Перейти обратно: ^а ^б ^с ^д Кромвель, Питер Р. (1997), Многогранники , издательство Кембриджского университета , стр. 91, ISBN 978-0-521-55432-9 .

[johnson-2] Jump up to: Перейти обратно: ^а ^б Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Canadian Journal of Mathematics , 18 : 169–200, doi : 10.4153/cjm-1966-021-8 , MR 0185507 , S2CID 122006114 , Zbl 0132.14603 .

[berman-3] Jump up to: Перейти обратно: ^а ^б ^с ^д Берман, Мартин (1971), «Выпуклые многогранники с правильными гранями», Журнал Института Франклина , 291 (5): 329–352, doi : 10.1016/0016-0032(71)90071-8 , MR 0290245 .

[francis-4] Фрэнсис, Дэррил (август 2013 г.), «Твердые тела Джонсона и их сокращения» , Word Ways , 46 (3): 177 .

[sommerville-5] Соммервилль, ДМЙ (1905), «Полурегулярные сети плоскости в абсолютной геометрии» , Труды Королевского общества Эдинбурга , 41 : 725–747, doi : 10.1017/s0080456800035560 . Цитируется Грюнбаумом (2009) .

[ball-6] Болл, Роуз (1939), Коксетер, HSM (ред.), Математические воссоздания и эссе (11-е изд.), стр. 137 .

[grunbaum-7] Jump up to: Перейти обратно: ^а ^б Грюнбаум, Бранко (2009), «Непреходящая ошибка» (PDF) , Elemente der Mathematik , 64 (3): 89–101, doi : 10.4171/EM/120 , MR 2520469 Перепечатано в Питичи, Мирча, изд. (2011). Лучшее сочинение по математике 2010 года . Издательство Принстонского университета. стр. 18–31. .

[lz-8] Ландо, Сергей К.; Звонкин, Александр К. (2004), Графы на поверхностях и их применение , Springer, с. 114, номер домена : 10.1007/978-3-540-38361-1 , ISBN. 978-3-540-38361-1 .

[9] «Соты J37» , Галерея деревянных многогранников , получено 21 марта 2016 г.

[10] Гринвуд, Норман Н .; Эрншоу, Алан (1997). Химия элементов (2-е изд.). Баттерворт-Хайнеманн . п. 986. ИСБН 978-0-08-037941-8 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

v т и Твердые вещества Джонсона
Пирамиды , купола и круги	квадратная пирамида пятиугольная пирамида треугольный купол квадратный купол пятиугольный купол пятиугольная ротонда
Модифицированные пирамиды	вытянутая треугольная пирамида вытянутая квадратная пирамида вытянутая пятиугольная пирамида Гироудлиненная квадратная пирамида гироудлиненная пятиугольная пирамида треугольная бипирамида пятиугольная бипирамида вытянутая треугольная бипирамида вытянутая квадратная бипирамида вытянутая пятиугольная бипирамида гироудлиненная квадратная бипирамида
Модифицированные купола и раунды	удлиненный треугольный купол вытянутый квадратный купол удлиненный пятиугольный купол вытянутая пятиугольная ротонда гироудлинённый треугольный купол гироудлиненный квадратный купол гироудлиненный пятиугольный купол гироудлиненная пятиугольная ротонда гиробифастигий треугольный ортобикупол квадратный ортобикупол квадратный гиробикупол пятиугольный ортобикупол пятиугольный гирокупол пятиугольная ортокуполаротонда пятиугольная гирокуполаротонда пятиугольная ортобиротонда удлиненный треугольный ортобикупол удлиненный треугольный гиробикупол вытянутый квадратный гиробикупол удлиненный пятиугольный ортобикупол удлиненный пятиугольный гиробикупол вытянутая пятиугольная ортокуполаротонда вытянутая пятиугольная гирокуполаротонда вытянутая пятиугольная ортобиротонда вытянутая пятиугольная гиробиротунда гироудлиненный треугольный двуглавый купол гироудлиненный квадратный двуглавый купол гироудлиненный пятиугольный двуглавый купол гироудлинённый пятиугольный купол-ротонда гироудлиненная пятиугольная биротонда
Дополненные призмы	увеличенная треугольная призма смещенная треугольная призма триаугментированная треугольная призма увеличенная пятиугольная призма увеличенная пятиугольная призма дополненная шестиугольная призма парабиоувеличенная шестиугольная призма метаувеличенная шестиугольная призма трехугольная шестиугольная призма
Модифицированные платоновые тела	дополненный додекаэдр парабиоувеличенный додекаэдр метаувеличенный додекаэдр триаугментированный додекаэдр метабидиминированный икосаэдр трехмерный икосаэдр увеличенный трехмерный икосаэдр
Модифицированные архимедовы тела	расширенный усеченный тетраэдр дополненный усеченный куб увеличенный усеченный куб расширенный усеченный додекаэдр парабиоувеличенный усеченный додекаэдр метаувеличенный усеченный додекаэдр триаугментированный усеченный додекаэдр вращающийся ромбокосододекаэдр парабигиратный ромбикосидодекаэдр метабивративный ромбокосододекаэдр тригиратный ромбикосидодекаэдр уменьшенный ромбокосододекаэдр парагиратный уменьшенный ромбикосидодекаэдр метавращающийся уменьшенный ромбокосододекаэдр большой, уменьшенный ромбокосододекаэдр парабидиуменьшенный ромбокосододекаэдр метабидиминированный ромбикосододекаэдр вращающийся двууменьшенный ромбокосододекаэдр трехмерный ромбикосидодекаэдр
Элементарные твердые тела	курносый дисфеноид курносая квадратная антипризма сфенокорона расширенная сфенокорона сфеномегакорона Гебесфеномегакорона дисфенозин коды неисправностей треугольная гебесфеноротонда
(См. также Список твердых тел Джонсона , сортируемую таблицу)