Невыпуклый большой ромбокубооктаэдр
| Невыпуклый большой ромбокубооктаэдр | |
|---|---|
 | |
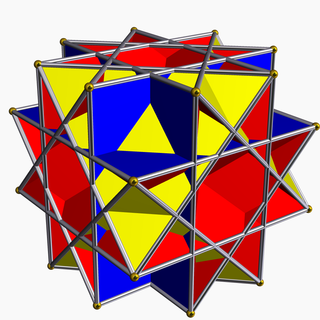| Тип | Однородный звездчатый многогранник |
| Элементы | Ф = 26, Е = 48 V = 24 (х = 2) |
| Лица по сторонам | 8{3}+(6+12){4} |
| Диаграмма Кокстера |       |
| Символ Витхоффа | 3/2 4 | 2 3 4/3 | 2 |
| Группа симметрии | О ч , [4,3], *432 |
| Ссылки на индексы | Ю 17 , Ц 59 , Ж 85 |
| Двойной многогранник | Большой дельтовидный икоситетраэдр |
| Вершинная фигура |  4.4.4.3/2 |
| Аббревиатура Бауэрса | Кверко |
В геометрии невыпуклый большой ромбокубооктаэдр представляет собой невыпуклый однородный многогранник , имеющий индекс U 17 . У него 26 граней (8 треугольников и 18 квадратов ), 48 ребер и 24 вершины. [1] Он представлен символом Шлефли rr{4, 3 ⁄ 2 } и Кокстера-Динкина диаграмма 
. Его вершинная фигура представляет собой перекрещенный четырехугольник .
Эта модель разделяет название с выпуклым большим ромбокубооктаэдром , также называемым усеченным кубооктаэдром .
Альтернативное название этой фигуры — квазиромбокубооктаэдр . Отсюда и происходит аббревиатура Бауэрса: querco .
Орфографические проекции
[ редактировать ]
Декартовы координаты
[ редактировать ]Декартовы координаты вершин невыпуклого большого ромбокубооктаэдра с центром в начале координат и длиной ребра 1 — это все перестановки
![{\displaystyle {\Bigl (}\pm \left[{\sqrt {2}}-1\right],\ \pm 1, \ \pm 1 {\Bigr)}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63a0eb05a516aefe295522e6d980b239bf14df0e)
Связанные многогранники
[ редактировать ]Он разделяет расположение вершин с выпуклым усеченным кубом . Кроме того, он имеет общее расположение ребер с большим кубооктаэдром (имеющим общие треугольные грани и 6 квадратных граней) и с большим ромбогексаэдром (имеющим 12 общих квадратных граней). Он имеет ту же фигуру вершины, что и псевдобольшой ромбокубооктаэдр , который не является однородным многогранником.
 Усеченный куб |  Большой ромбокубооктаэдр |  Большой кубический октаэдр |  Большой ромбогексаэдр |  Псевдобольшой ромбокубооктаэдр |
Большой дельтовидный икоситетраэдр
[ редактировать ]| Большой дельтовидный икоситетраэдр | |
|---|---|
 | |
| Тип | Звездный многогранник |
| Лицо |  |
| Элементы | Ф = 24, Е = 48 V = 26 (χ = 2) |
| Группа симметрии | О ч , [4,3], *432 |
| Ссылки на индексы | ДУ 17 |
| двойной многогранник | Невыпуклый большой ромбокубооктаэдр |
Большой дельтовидный икоситетраэдр является двойником невыпуклого большого ромбокубооктаэдра.
Ссылки
[ редактировать ]- ^ Медер, Роман. «17: большой ромбокубооктаэдр» . МатКонсалт .
- Веннингер, Магнус (1983), Двойные модели , Издательство Кембриджского университета , номер документа : 10.1017/CBO9780511569371 , ISBN 978-0-521-54325-5 , МР 0730208
Внешние ссылки
[ редактировать ]Вайсштейн, Эрик В. «Большой дельтовидный икоситетраэдр» . Математический мир .
- Вайсштейн, Эрик В. «Однородный большой ромбокубооктаэдр» . Математический мир .
- Большой ромбокубооктаэдр Бумажная модель
 | Эта многогранникам, статья, посвященная незавершена . Вы можете помочь Википедии, расширив ее . |