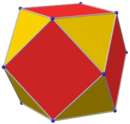
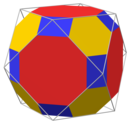
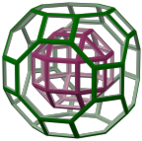
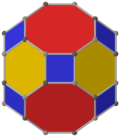
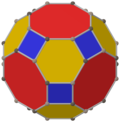
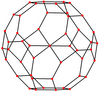
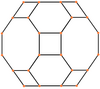
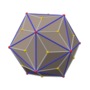
Усеченный кубооктаэдр

Усеченный кубооктаэдр
(Нажмите здесь, чтобы увидеть вращающуюся модель)
Тип	Архимедово тело Однородный многогранник
Элементы	F = 26, E = 72, V = 48 (χ = 2)
Лица по сторонам	12{4}+8{6}+6{8}
Обозначение Конвея	bC или taC
Символы Шлефли	tr{4,3} или $t{\begin{Bmatrix}4\\3\end{Bmatrix}}$
	т 0,1,2 {4,3}
Символ Витхоффа	2 3 4 |
Диаграмма Кокстера
Группа симметрии	О h , B 3 , [4,3], (*432), порядок 48
Группа ротации	О , [4,3] + , (432), порядок 24
Двугранный угол	${\begin{aligned}{\text{4-6:}}&\ \arccos {\tfrac {-{\sqrt {6}}}{3}}=144^{\circ }44'08''\\[4pt]{\text{4-8:}}&\ \arccos {\tfrac {-1}{\sqrt {2}}}=135^{\circ }\\{\text{6-8:}}&\ \arccos {\tfrac {-{\sqrt {3}}}{3}}=125^{\circ }15'51''\end{aligned}}$
Ссылки	Ю 11 , С 23 , Ж 15
Характеристики	Полуправильный выпуклый зоноэдр
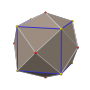
Цветные лица	4.6.8 ( фигура вершины )
Додекаэдр Дисдякиса ( двойной многогранник )	Сеть

В геометрии или усеченный кубооктаэдр большой ромбокубооктаэдр собой архимедово тело , названное Кеплером усечением кубооктаэдра . представляет Он имеет 12 квадратных граней, 8 правильных шестиугольных граней, 6 правильных восьмиугольных граней, 48 вершин и 72 ребра. Поскольку каждая из его граней имеет точечную симметрию (что эквивалентно вращательной симметрии 180°), усеченный кубооктаэдр представляет собой 9 - зоноэдр . Усеченный кубооктаэдр может мозаично сочетаться с восьмиугольной призмой .

Имена

Название усеченный кубооктаэдр данное Иоганном Кеплером , вводит в заблуждение: фактическое усечение кубооктаэдра , первоначально имеет прямоугольники вместо квадратов ; однако этот неоднородный многогранник топологически эквивалентен архимедову телу, не совсем строго названному усеченным кубооктаэдром. Альтернативные взаимозаменяемые названия: Усеченный кубооктаэдр ( Иоганн Кеплер ), Ромбоусечённый кубооктаэдр ( Магнус Веннингер) . ), Большой ромбокубооктаэдр ( Роберт Уильямс) ), Большой ромбокубооктаэдр (Питер Кромвель) ), Всеусеченный куб или кантиусеченный куб ( Норман Джонсон ), Скошенный куб ( обозначение многогранника Конвея ).

Кубооктаэдр и его усечение.

Существует невыпуклый однородный многогранник с похожим названием: невыпуклый большой ромбокубооктаэдр .

Декартовы координаты

Декартовы координаты вершин усеченного кубооктаэдра с длиной ребра 2 и центром в начале координат представляют собой все перестановки :

$${\Bigl (}\pm 1,\quad \pm \left(1+{\sqrt {2}}\right),\quad \pm \left(1+2{\sqrt {2}}\right){\Bigr )}.$$

Площадь и объём

Площадь A и объем V усеченного кубооктаэдра с длиной ребра a равны:

${\begin{aligned}A&=12\left(2+{\sqrt {2}}+{\sqrt {3}}\right)a^{2}&&\approx 61.755\,1724~a^{2},\\V&=\left(22+14{\sqrt {2}}\right)a^{3}&&\approx 41.798\,9899~a^{3}.\end{aligned}}$

Рассечение

Усеченный кубооктаэдр — это оболочка ромбокубооктаэдра выпуклая с кубами над 12 квадратами на осях симметрии 2-го порядка. Остальное его пространство можно разделить на 6 квадратных куполов под восьмиугольниками и 8 треугольных куполов под шестиугольниками.

Рассеченный усеченный кубооктаэдр может создать тороид Стюарта рода 5, 7 или 11 , удалив центральный ромбокубооктаэдр и либо 6 квадратных куполов, 8 треугольных куполов или 12 кубов соответственно. Многие другие тороиды с более низкой симметрией также могут быть построены путем удаления центрального ромбокубооктаэдра и подмножества других компонентов рассечения. Например, удаление четырех треугольных куполов создает тороид рода 3; если эти купола выбраны соответствующим образом, то этот тороид имеет тетраэдрическую симметрию.

showТороиды Стюарта
Genus 3	Genus 5	Genus 7	Genus 11

Равномерные раскраски

Существует только одна единая раскраска граней этого многогранника, по одному цвету для каждого типа грани.

2-однородная раскраска с тетраэдрической симметрией существует для шестиугольников попеременного цвета.

Ортогональные проекции

Усеченный кубооктаэдр имеет две специальные ортогональные проекции A ₂ и B ₂ в плоскостях Кокстера с проективной симметрией [6] и [8], а многочисленные симметрии [2] могут быть построены из различных проекций плоскостей относительно элементов многогранника.

Ортогональные проекции

В центре	Вертекс	Край 4-6	Край 4-8	Край 6-8	Лицо нормальное 4-6
Изображение
Проективный симметрия	[2] +	[2]	[2]	[2]	[2]
В центре	Лицо нормальное Квадрат	Лицо нормальное Октагон	Лицо Квадрат	Лицо Шестиугольник	Лицо Октагон
Изображение
Проективный симметрия	[2]	[2]	[2]	[6]	[4]

Сферическая черепица

Усеченный кубооктаэдр также можно представить в виде сферической мозаики и спроецировать на плоскость с помощью стереографической проекции . Эта проекция является равноугольной , сохраняющей углы, но не площади или длины. Прямые линии на сфере проецируются на плоскость в виде дуг окружностей.

Ортогональная проекция	квадратно -центрированный	шестиугольник с центром	восьмиугольник с центром
	Стереографические проекции

Полная

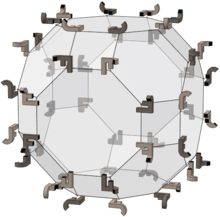
Как и многие другие твердые тела, усеченный октаэдр обладает полной октаэдрической симметрией , но его связь с полной октаэдрической группой более тесная: его 48 вершин соответствуют элементам группы, а каждая грань его двойника является фундаментальной областью группы.

Изображение справа показывает 48 перестановок в группе, примененных к примеру объекта (а именно к легкому соединению JF слева). 24 светлых элемента — это вращения, а темные — их отражения.

Края тела соответствуют 9 отражениям в группе:

• Те, что между восьмиугольниками и квадратами, соответствуют трем отражениям между противоположными восьмиугольниками.
• Ребра шестиугольника соответствуют 6 отражениям между противоположными квадратами.
• (Между противоположными шестиугольниками нет отражений.)

Подгруппы соответствуют телам, имеющим общие вершины усеченного октаэдра.
Например, 3 подгруппы с 24 элементами соответствуют неоднородному курносому кубу с киральной октаэдрической симметрией, неоднородному ромбокубооктаэдру с пиритоэдрической симметрией ( кантический курносый октаэдр ) и неоднородному усеченному октаэдру с полной тетраэдрической симметрией . Единственная подгруппа из 12 элементов — это знакопеременная группа A ₄ . Он соответствует неоднородному икосаэдру с киральной тетраэдрической симметрией .

скрывать Подгруппы и соответствующие им твердые тела
Усеченный кубооктаэдр тр{4,3}	Курносый куб ср{4,3}	Ромбокубооктаэдр с2 { 3,4}	Усеченный октаэдр ч 1,2 {4,3}	Икосаэдр
[4,3] Полный октаэдрический	[4,3] + Хиральный октаэдр	[4,3 + ] Пиритоэдрический	[1 + ,4,3] = [3,3] Полный тетраэдр	[1 + ,4,3 + ] = [3,3] + Хиральный тетраэдр
все 48 вершин	24 вершины			12 вершин

Связанные многогранники

Тетраэдр-бабочка и куб содержат две трапециевидные грани вместо каждого квадрата.

Усечённый кубооктаэдр — один из семейства однородных многогранников, родственных кубу и правильному октаэдру.

showОднородные октаэдрические многогранники
Symmetry: [4,3], (*432)							[4,3]+ (432)	[1+,4,3] = [3,3] (*332)		[3+,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{31,1}	t{3,4} t{31,1}	{3,4} {31,1}	rr{4,3} s2{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	s{3,4} s{31,1}
		=	=	=				= or	= or	=
Duals to uniform polyhedra
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

Этот многогранник можно считать членом последовательности однородных узоров с конфигурацией вершин (4.6.2 p ) и диаграммой Кокстера-Дынкина. . Для p < 6 членами последовательности являются всеусеченные многогранники ( зоноэдры ), показанные ниже в виде сферических мозаик. При p < 6 они представляют собой мозаику гиперболической плоскости, начиная с усеченной трехгептагональной мозаики .

show* n 32 мутация симметрии всеусеченных мозаик: 4.6.2n
Sym. *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paraco.	Noncompact hyperbolic
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Figures
Config.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duals
Config.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

show* n 42 мутация симметрии всеусеченных мозаик: 4.8.2n
Symmetry *n42 [n,4]	Spherical		Euclidean	Compact hyperbolic				Paracomp.
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Omnitruncated figure	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞
Omnitruncated duals	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞

show* n 32 мутация симметрии всеусеченных мозаик: 6.8.2n
Sym. *n43 [(n,4,3)]	Spherical	Compact hyperbolic						Paraco.
	*243 [4,3]	*343 [(3,4,3)]	*443 [(4,4,3)]	*543 [(5,4,3)]	*643 [(6,4,3)]	*743 [(7,4,3)]	*843 [(8,4,3)]	*∞43 [(∞,4,3)]
Figures
Config.	4.8.6	6.8.6	8.8.6	10.8.6	12.8.6	14.8.6	16.8.6	∞.8.6
Duals
Config.	V4.8.6	V6.8.6	V8.8.6	V10.8.6	V12.8.6	V14.8.6	V16.8.6	V6.8.∞

Это первый в серии усеченных гиперкубов:

полигонов Петри Проекции

Усеченный кубооктаэдр	Кантитусеченный тессеракт	Количественный усеченный 5-куб	Количественный усеченный 6-куб	Количественный усеченный 7-куб	Количественный усеченный 8-куб

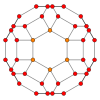
Усеченный кубооктаэдрический граф

Усеченный кубооктаэдрический граф
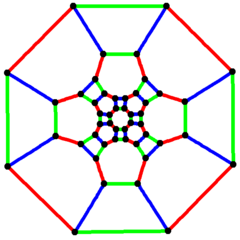4-кратная симметрия
Вершины	48
Края	72
Автоморфизмы	48
Хроматическое число	2
Характеристики	Кубический , гамильтонов , регулярный , нуль-симметричный
Таблица графиков и параметров

В математической области теории графов усеченный кубооктаэдрический граф (или большой ромбокубооктаэдрический граф ) — это график вершин и ребер усеченного кубооктаэдра, одного из архимедовых тел . Он имеет 48 вершин ребра и представляет собой нуль-симметричный кубический и 72 архимедов граф .

См. также

• Куб
• Кубооктаэдр
• Октаэдр
• Усеченный икосододекаэдр
• Усеченный октаэдр – усеченный тетраэдр.
• Курносый куб

Ссылки

• Кромвель, П. (1997). Многогранники . Великобритания: Кембридж. С. 79–86 Архимедовы тела . ISBN  0-521-55432-2 .

Внешние ссылки

• Вайсштейн, Эрик В. , « Большой ромбокубооктаэдр » (« Архимедово тело ») в MathWorld .
  • Вайсштейн, Эрик В. «Великий ромбокубооктаэдрический граф» . Математический мир .
• Клитцинг, Ричард. «3D выпуклые однородные многогранники x3x4x — гирко» .
• Редактируемая для печати сетка усеченного кубооктаэдра с интерактивным 3D-просмотром
• Однородные многогранники
• Многогранники виртуальной реальности Энциклопедия многогранников
• Большой ромбокубооктаэдр: бумажные полоски для плетения