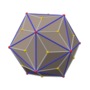
Ромбокубооктаэдр

«Расширенный октаэдр» перенаправляется сюда. О структуре тенсегрити см. Икосаэдр Джессена .

Ромбокубооктаэдр
Тип	Архимед Однородный многогранник
Лица	26
Края	48
Вершины	24
Конфигурация вершин	$24(3\cdot 4^{3})$
Группа симметрии	Октаэдрическая симметрия $\mathrm {O} _{\mathrm {h} }$
Двойной многогранник	Дельтоидный икоситетраэдр
Вершинная фигура
Сеть

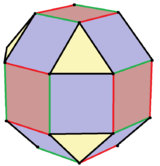
В геометрии ромбокубооктаэдр квадратными , или малый ромбокубооктаэдр , представляет собой многогранник с восемью треугольными , шестью и двенадцатью прямоугольными гранями. Имеется 24 одинаковых вершины, в каждой из которых встречаются по одному треугольнику, одному квадрату и двум прямоугольникам. треугольников Если все прямоугольники сами по себе квадратные (то есть все ребра имеют одинаковую длину, что гарантирует равносторонность ), это архимедово тело . Многогранник обладает октаэдрической симметрией , как куб и октаэдр . Его двойник называется дельтовидным икоситетраэдром или трапециевидным икоситетраэдром, хотя его грани на самом деле не являются настоящими трапециями .

Имена

Иоганн Кеплер в своей книге «Harmonices Mundi» 1618 года назвал этот многогранник ромбокубооктаэдром , что является сокращением от усеченного кубооктаэдрического ромба , причем кубооктаэдрический ромб был его именем для ромбического додекаэдра . Существуют различные варианты усечения ромбододекаэдра в топологический ромбокубооктаэдр: в первую очередь его выпрямление (слева), то, которое создает однородное твердое тело (в центре), и выпрямление двойного кубооктаэдра (справа), которое является ядром двойного соединения. .

Его также можно назвать расширенным или согнутым кубом или октаэдром , из-за операций усечения любого однородного многогранника .

Геометрические отношения

Ромбикубооктаэдр можно рассматривать либо как расширенный куб (синие грани), либо как расширенный октаэдр (красные грани).

Существуют искажения ромбокубооктаэдра, который, хотя некоторые грани не являются правильными многоугольниками, все же являются однородными по вершинам. Некоторые из них можно сделать, взяв куб или октаэдр и отрезав края, а затем обрезав углы, так что в результате получится многогранник с шестью квадратными и двенадцатью прямоугольными гранями. Они имеют октаэдрическую симметрию и образуют непрерывный ряд между кубом и октаэдром, аналогичный искажениям ромбокосододекаэдра или тетраэдрическим искажениям кубооктаэдра . Однако ромбокубооктаэдр также имеет второй набор искажений с шестью прямоугольными и шестнадцатью трапециевидными гранями, которые обладают не октаэдрической симметрией, а скорее _{симметрией Th} , поэтому они инвариантны при тех же вращениях, что и тетраэдр, но при других отражениях.

Линии, по которым кубик Рубика можно поворачивать , проецируются на сферу, подобную, топологически идентичную ребрам ромбокубооктаэдра. Фактически, были созданы варианты с использованием механизма кубика Рубика, которые очень напоминают ромбокубооктаэдр.

Ромбокубооктаэдр используется в трех однородных мозаиках, заполняющих пространство : зубчатые кубические соты , усеченные кубические соты и суженные чередующиеся кубические соты .

Рассечение

Ромбокубооктаэдр можно разделить на два квадратных купола и центральную восьмиугольную призму . Поворот одного купола на 45 градусов создает псевдоромбокубооктаэдр . Оба этих многогранника имеют одну и ту же фигуру вершины: 3.4.4.4.

Треугольники расположены в шахматном порядке в псевдоромбокубооктаэдре (вверху), но выровнены в ромбокубооктаэдре (внизу).

Есть три пары параллельных плоскостей, каждая из которых пересекает ромбокубооктаэдр в правильном восьмиугольнике. Ромбокубооктаэдр можно разделить по любому из них, чтобы получить восьмиугольную призму с правильными гранями и двумя дополнительными многогранниками, называемыми квадратными куполами , которые относятся к телам Джонсона ; Таким образом, это удлиненный квадратный орто- двуглавый купол . Эти части можно собрать заново, чтобы получить новое твердое тело, называемое удлиненным квадратным гиробикуполом или псевдоромбокубооктаэдром , с симметрией квадратной антипризмы. В этом случае все вершины локально такие же, как у ромбокубооктаэдра, в каждой из которых встречаются один треугольник и три квадрата, но не все они идентичны относительно всего многогранника, поскольку некоторые из них расположены ближе к оси симметрии, чем другие.

	Ромбокубооктаэдр
	Псевдоромбокубооктаэдр

Ортогональные проекции

Ромбикубооктаэдр . имеет шесть особых ортогональных проекций , центрированных на вершине, на двух типах ребер и трех типах граней: треугольниках и двух квадратах Последние два соответствуют _{B 2} и A ₂ плоскостям Кокстера .

Ортогональные проекции

В центре	Вертекс	Край 3-4	Край 4-4	Лицо Площадь-1	Лицо Площадь-2	Лицо Треугольник
Твердый
Каркас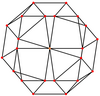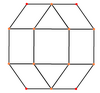
Проективный симметрия	[2]	[2]	[2]	[2]	[4]	[6]
Двойной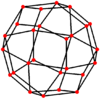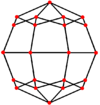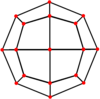

Сферическая черепица

Ромбикубооктаэдр также можно представить в виде сферической мозаики и спроецировать на плоскость с помощью стереографической проекции . Эта проекция является равноугольной , сохраняющей углы, но не площади или длины. Прямые линии на сфере проецируются на плоскость в виде дуг окружностей.

	(6) квадратно -центрированный	(6) квадратно -центрированный	(8) треугольник по центру
Ортогональная проекция	Стереографические проекции

Пиритоэдрическая симметрия

Полусимметричная форма ромбокубооктаэдра. , существует с пиритоэдрической симметрией , [4,3 ⁺ ], (3*2) как диаграмма Кокстера , символ Шлефли s ₂ {3,4}, и его можно назвать кантическим курносым октаэдром . Эту форму можно визуализировать, поочередно раскрашивая края шести квадратов . Эти квадраты затем можно превратить в прямоугольники , при этом 8 треугольников останутся равносторонними. 12 диагональных квадратных граней станут равнобедренными трапециями . В пределе прямоугольники можно свести к ребрам, а трапеции превратить в треугольники и икосаэдр образовать , за счет курносой конструкции октаэдра . , с{3,4}. ( Соединение двух икосаэдров построено из обоих чередующихся положений.)

showВариации пиритоэдрической симметрии
Uniform geometry	Nonuniform geometry	Nonuniform geometry	In the limit, an icosahedron snub octahedron, , from one of two positions.	Compound of two icosahedra from both alternated positions.

Алгебраические свойства

Декартовы координаты

Декартовы координаты вершин ромбокубооктаэдра с центром в начале координат и длиной ребра 2 единицы представляют собой все четные перестановки

(±1, ±1, ±(1 + √ 2 )).

Если исходный ромбокубооктаэдр имеет единичную длину ребра, его двойной стромбический икоситетраэдр имеет длины ребер.

${\frac {2}{7}}{\sqrt {10-{\sqrt {2}}}}\quad {\text{and}}\quad {\sqrt {4-2{\sqrt {2}}}}.$

Площадь и объём

Площадь A и объем V ромбокубооктаэдра с длиной ребра a равны:

${\begin{aligned}A&=\left(18+2{\sqrt {3}}\right)a^{2}&&\approx 21.464\,1016a^{2}\\V&={\frac {12+10{\sqrt {2}}}{3}}a^{3}&&\approx 8.714\,045\,21a^{3}.\end{aligned}}$

Плотность плотной упаковки

Оптимальная доля упаковки ромбокубооктаэдров определяется выражением

$\eta ={\tfrac {4}{3}}\left(4{\sqrt {2}}-5\right)$.

Было замечено, что это оптимальное значение получено в решетке Браве де Граафом ( 2011 ). Поскольку ромбокубооктаэдр содержится в ромбододекаэдре , которого вписанная сфера идентична его собственной вписанной сфере, значение оптимальной доли упаковки является следствием гипотезы Кеплера : этого можно достичь, поместив ромбокубооктаэдр в каждую ячейку ромбододекаэдра . сот , и превзойти ее невозможно, так как в противном случае оптимальную плотность упаковки сфер можно было бы превзойти, поместив сферу в каждый ромбокубооктаэдр превосходящей ее гипотетической упаковки.

В искусстве

Портрет Луки Пачоли (ок. 1495 г.)

Леонардо да Винчи Иллюстрация к «Божественной пропорции» (1509 г.)

1495 года Портрет Луки Пачоли , традиционно приписываемый Якопо де Барбари , включает в себя стеклянный ромбокубооктаэдр, наполовину наполненный водой, который, возможно, был написан Леонардо да Винчи . Первая печатная версия ромбокубооктаэдра была написана Леонардо и появилась в ( Пачоли «Божественной пропорции» 1509).

Сферическую панораму размером 180×360° можно спроецировать на любой многогранник; но ромбокубооктаэдр достаточно хорошо приближает сферу, но при этом его легко построить. Этот тип проекции, называемый «Филосфера» , возможен с помощью некоторых программ для сборки панорам. Он состоит из двух изображений, которые распечатываются отдельно и вырезаются ножницами, оставляя несколько лоскутов для сборки с помощью клея.

Объекты

Во время повального увлечения кубиком Рубика в 1980-х годах по крайней мере две проданные извилистые головоломки имели форму ромбокубооктаэдра (механизм был похож на механизм кубика Рубика ).

• 
  Солнечные часы (1596 г.)
• 
  Солнечные часы
• 
  Уличный фонарь в Майнце
• 
  Умрите с 18 помеченными гранями
• 
  Кабелы Мишень для стрельбы
• 
  Змея Рубика
• 
  Вариант кубика Рубика
• 
  пирита Кристалл

Связанные многогранники

Ромбикубооктаэдр — один из семейства однородных многогранников, родственных кубу и правильному октаэдру.

showОднородные октаэдрические многогранники
Symmetry: [4,3], (*432)							[4,3]+ (432)	[1+,4,3] = [3,3] (*332)		[3+,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{31,1}	t{3,4} t{31,1}	{3,4} {31,1}	rr{4,3} s2{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	s{3,4} s{31,1}
		=	=	=				= or	= or	=
Duals to uniform polyhedra
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

Мутации

Этот многогранник топологически связан как часть последовательности сочлененных многогранников с фигурой вершины (3.4.n.4 ) и продолжается как мозаика гиперболической плоскости . Эти вершинно-транзитивные фигуры обладают (* n 32) отражательной симметрией .

show* n 32 мутация симметрии развернутых мозаик: 3.4. № .4
Symmetry *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paracomp.
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Figure
Config.	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4	3.4.7.4	3.4.8.4	3.4.∞.4

show* n 42 мутация симметрии расширенных мозаик: n .4.4.4
Symmetry [n,4], (*n42)	Spherical	Euclidean	Compact hyperbolic				Paracomp.
	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]	*∞42 [∞,4]
Expanded figures
Config.	3.4.4.4	4.4.4.4	5.4.4.4	6.4.4.4	7.4.4.4	8.4.4.4	∞.4.4.4
Rhombic figures config.	V3.4.4.4	V4.4.4.4	V5.4.4.4	V6.4.4.4	V7.4.4.4	V8.4.4.4	V∞.4.4.4

Расположение вершин

Он разделяет расположение вершин с тремя невыпуклыми однородными многогранниками : звездчатым усеченным шестигранником , малым ромбошестигранником (имеющим общие треугольные грани и шесть квадратных граней) и маленьким кубооктаэдром (имеющим двенадцать общих квадратных граней).

Ромбокубооктаэдр

Малый кубический октаэдр

Малый ромбошестигранник

Звездчатый усеченный шестигранник

Ромбокубооктаэдрический граф
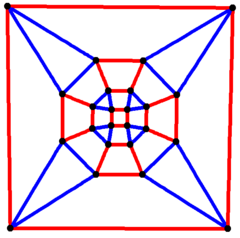4-кратная симметрия
Вершины	24
Края	48
Автоморфизмы	48
Характеристики	Граф четвертой степени , гамильтониан , регулярный
Таблица графиков и параметров

Ромбокубооктаэдрический граф

Ромбикубооктаэдрический граф — это граф вершин и ребер ромбокубооктаэдра. Он имеет 24 вершины и 48 ребер и является четвертой степени архимедовым графом .

См. также

• Соединение пяти ромбокубооктаэдров.
• Куб
• Кубооктаэдр
• Невыпуклый большой ромбокубооктаэдр
• Усеченный ромбокубооктаэдр
• Вытянутый квадратный гиробикупол.
• Моравская звезда
• Октаэдр
• Ромбикосидодекаэдр
• Змея Рубика - головоломка, из которой можно сформировать «шар» в виде ромбокубооктаэдра.
• Национальная библиотека Беларуси – ее основная архитектурная составляющая имеет форму ромбокубооктаэдра.
• Усеченный кубооктаэдр (большой ромбокубооктаэдр)

Дальнейшее чтение

• Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN  0-486-23729-Х . (Раздел 3–9)
• Кромвель, П. (1997). Многогранники . Великобритания: Кембридж. С. 79–86 Архимедовы тела . ISBN  0-521-55432-2 .
• Коксетер, HSM ; Лонге-Хиггинс, MS; Миллер, JCP (13 мая 1954 г.). «Равномерные многогранники». Философские труды Лондонского королевского общества. Серия А, Математические и физические науки . 246 (916): 401–450. Бибкод : 1954RSPTA.246..401C . дои : 10.1098/rsta.1954.0003 . S2CID   202575183 .
• де Грааф, Дж.; ван Рой, Р.; Дейкстра, М. (2011), «Плотные регулярные упаковки неправильных невыпуклых частиц», Physical Review Letters , 107 (15): 155501, arXiv : 1107.0603 , Bibcode : 2011PhRvL.107o5501D , doi : 10.1103/PhysRevLett.107 .155501 , PMID   22107298 , S2CID   14041658
• Бетке, У.; Хенк, М. (2000), «Самые плотные решетчатые упаковки 3-многогранников», Вычислительная геометрия , 16 (3): 157–186, arXiv : math/9909172 , doi : 10.1016/S0925-7721(00)00007-9
• Торквато, С.; Цзяо, Ю. (2009), «Плотные упаковки платоновых и архимедовых тел», Nature , 460 (7257): 876–879, arXiv : 0908.4107 , Bibcode : 2009Natur.460..876T , doi : 10.1038/nature08239 , PMID   19675649 , S2CID   52819935
• Хейлз, Томас К. (2005), «Доказательство гипотезы Кеплера», Annals of Mathematics , 162 (3): 1065–1185, arXiv : math/9811078v2 , doi : 10.4007/annals.2005.162.1065

Внешние ссылки

• Вайсштейн, Эрик В. , « Ромбокубооктаэдр » (« Архимедово тело ») в MathWorld .
  • Вайсштейн, Эрик В. «Маленький ромбокубооктаэдрический граф» . Математический мир .
• Клитцинг, Ричард. «3D выпуклые однородные многогранники x3o4x — сирко» .
• Однородные многогранники
• Многогранники виртуальной реальности Энциклопедия многогранников
• Редактируемая для печати сетка ромбокубооктаэдра с интерактивным 3D-просмотром
• Звезда ромбокубооктаэдра, автор Шандор Кабай, Демонстрационный проект Вольфрама .
• Ромбокубооктаэдр: бумажные полоски для плетения