Соты (геометрия)

В геометрии соты — это заполнение пространства или плотная упаковка ячеек многогранных более высокой размерности или ячеек , так что не остается пробелов. Это пример более общего математического разбиения или мозаики в любом количестве измерений. Его размерность можно уточнить как n -соту для соты n -мерного пространства.

Соты обычно строятся в обычном евклидовом («плоском») пространстве. Они также могут быть построены в неевклидовых пространствах , таких как гиперболические соты . Любой конечный однородный многогранник можно спроецировать на его описанную сферу, чтобы сформировать однородную соту в сферическом пространстве.

Классификация

Существует бесконечно много сот, которые классифицированы лишь частично. Наибольший интерес вызвали более регулярные, в то время как продолжает открываться богатый и разнообразный ассортимент других.

Простейшие соты формируются из сложенных друг на друга слоев или плит призм , основанных на некоторых мозаиках плоскости. В частности, для каждого параллелепипеда копии могут заполнять пространство, причем кубические соты являются особенными, поскольку это единственные правильные соты в обычном (евклидовом) пространстве. Еще одно интересное семейство — тетраэдры Хилла и их обобщения, которые также могут замостить пространство.

Равномерное 3-соты

Трехмерные однородные соты — это соты в трехмерном пространстве , состоящие из однородных многогранных ячеек и имеющие одинаковые вершины (т. е. группа [изометрий трехмерного пространства, сохраняющих мозаику] транзитивна на вершинах ). 28 выпуклых примеров. В евклидовом трехмерном пространстве ^[1] также называемые архимедовыми сотами .

Соты называются регулярными , если группа изометрий, сохраняющих замощение, действует транзитивно на флагах, где флагом является вершина, лежащая на ребре, лежащем на грани, лежащей на ячейке. Любые обычные соты автоматически становятся однородными. Однако в евклидовом трехмерном пространстве есть только одна правильная сота — кубическая сота . Два являются квазирегулярными (состоящими из двух типов правильных ячеек):

Тип	Обычные кубические соты	Квазирегулярные соты
Клетки	Кубический	Октаэдры и тетраэдры
Слой плиты

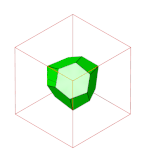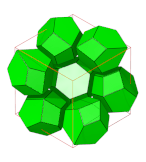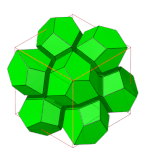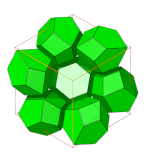
Тетраэдрально -октаэдрические соты и вращающиеся тетраэдрально-октаэдрические соты образуются из 3 или 2 положений пластинчатого слоя ячеек, в каждом из которых чередуются тетраэдры и октаэдры. Бесконечное количество уникальных сот может быть создано с помощью шаблонов более высокого порядка повторения этих слоев плиты.

Многогранники, заполняющие пространство

Соты, в которых все ячейки идентичны в пределах своей симметрии, называются клеточно-транзитивными или изохорными . В трехмерном евклидовом пространстве ячейка такой соты называется заполняющим пространство многогранником . ^[2] того Необходимым условием , чтобы многогранник был многогранником, заполняющим пространство, является то, что его инвариант Дена должен быть равен нулю: ^[3]^[4] исключение любых платоновых тел, кроме куба.

Пять выпуклых многогранников, заполняющих пространство, могут замощить трехмерное евклидово пространство, используя только сдвиги. Их называют параллелоэдрами :

Кубические соты (или варианты: кубоид , ромбический шестигранник или параллелепипед )
Шестиугольные призматические соты ^[5]
Ромбические додекаэдрические соты
Удлиненные додекаэдрические соты ^[6]
Двуусеченные кубические соты или усеченные октаэдры ^[7]

Куб (параллелепипед)	Шестиугольная призма	Ромбический додекаэдр	Вытянутый додекаэдр	Усеченный октаэдр
кубические соты	Шестиугольные призматические соты	Ромбические додекаэдры	Удлиненные додекаэдры	Усеченные октаэдры

3 длины кромки	3+1 длины кромки	4 длины кромки	4+1 длины кромки	6 длин кромок

Другие известные примеры многогранников, заполняющих пространство, включают:

Треугольные призматические соты
Вращающиеся треугольные призматические соты.
Триакис представляет собой усеченные четырехгранные соты . Такую форму имеют ячейки Вороного атомов углерода в алмазе. ^[8]
Трапецоромбические додекаэдрические соты. ^[9]
Изоэдральные мозаики ^[10]

Прочие соты с двумя и более многогранниками

Иногда два ^[11] или несколько разных многогранников могут быть объединены для заполнения пространства. Помимо множества однородных сот, еще одним хорошо известным примером является структура Вейра-Фелана , заимствованная из структуры кристаллов клатратных гидратов. ^[12]

Периодическая единица структуры Вейра–Фелана .

Мозаика P8 (с левыми и правыми ячейками)

Соты из левой и правой версий одного и того же многогранника.

Невыпуклые 3-сотовые соты

Документированные примеры редки. Можно выделить два класса:

Невыпуклые ячейки, которые упаковываются без перекрытия, аналогично мозаике вогнутых многоугольников. К ним относится упаковка небольшого звездчатого ромбического додекаэдра , как в кубе Ёсимото .
Перекрытие ячеек, положительная и отрицательная плотности которых «уравновешиваются», образуя равномерно плотный континуум, аналогично перекрывающимся мозаикам плоскости.

Гиперболические соты

В трехмерном гиперболическом пространстве двугранный угол многогранника зависит от его размера. Таким образом, правильные гиперболические соты включают две с четырьмя или пятью додекаэдрами, сходящимися на каждом ребре; их двугранные углы, таким образом, равны π/2 и 2π/5, оба из которых меньше, чем у евклидова додекаэдра. Помимо этого эффекта, гиперболические соты подчиняются тем же топологическим ограничениям, что и евклидовы соты и полихора.

4 компактных и 11 паракомпактных правильных гиперболических сот, а также множество компактных и паракомпактных Перечислены однородных гиперболических сот.

Четыре регулярных компактных сот в формате H ³
{5,3,4}	{4,3,5}	{3,5,3}	{5,3,5}

11 паракомпактных стандартных сот
{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{4,4,3}	{4,4,4}
{3,3,6}	{4,3,6}	{5,3,6}	{3,6,3}	{3,4,4}

Двойственность 3-сот

На каждую соту приходится двойная сота, которую можно получить путем обмена:

ячейки для вершин.

грани для ребер.

Это всего лишь правила дуализации четырехмерных 4-многогранников , за исключением того, что обычный конечный метод возвратно-поступательного движения вокруг концентрической гиперсферы может столкнуться с проблемами.

Более регулярные соты аккуратно дуализируются:

Кубические соты самодвойственны.
Структура октаэдров и тетраэдров двойственна структуре ромбических додекаэдров.
Плитные соты, полученные из однородных плоских мозаик, двойственны друг другу так же, как и мозаики.
Все двойники остальных архимедовых сот являются клеточно-транзитивными и были описаны Инчбальдом. ^[13]

Самодвойные соты

Соты также могут быть самодвойственными . Все n -мерные гиперкубические соты с символами Шлефли {4,3 ^{п -2},4} самодвойственны.

См. также

Ссылки

^ Грюнбаум (1994). «Равномерные замощения трехмерного пространства». Геомбинаторика 4(2)
^ Вайсштейн, Эрик В. «Многогранник, заполняющий пространство» . Математический мир .
^ Дебруннер, Ханс Э. (1980), «О равенстве разложения многогранников тротуара с кубами», Archives of Mathematics (на немецком языке), 35 (6): 583–587, doi : 10.1007/BF01235384 , MR 0604258 , S2CID 121301319 .
^ Лагариас, JC ; Моьюс, Д. (1995), «Многогранники, заполняющие $\mathbb {R} ^{n}$ и конгруэнтность ножниц», «Дискретная и вычислительная геометрия» , 13 (3–4): 573–583, doi : 10.1007/BF02574064 , MR 1318797 .
^ [1] Равномерное заполнение пространства с использованием треугольных, квадратных и шестиугольных призм.
^ [2] Равномерное заполнение пространства с использованием только ромбо-шестиугольных додекаэдров.
^ [3] Равномерное заполнение пространства с использованием только усеченных октаэдров.
^ Джон Конвей (22 декабря 2003 г.). "Многогранник Вороного. геометрия.пазлы" . Группа новостей : geometry.puzzles . Usenet: Pine.LNX.4.44.0312221226380.25139-100000@fine318a.math.Princeton.EDU .
^ X. Цянь, Д. Страс и Т. Шлик, J. Comput. хим. 22 (15) 1843–1850 (2001)
^ [4] О. Дельгадо-Фридрихс и М. О'Киф. Изоэдральные простые замощения: бинодали и плитки с <16 гранями. Акта Кристаллогр. (2005) А61, 358-362
^ [5] Архивировано 30 июня 2015 г. в Wayback Machine Gabbrielli, Руджеро. Тринадцатигранный многогранник, заполняющий пространство своей киральной копией.
^ Полинг, Лайнус. Природа химической связи. Издательство Корнелльского университета, 1960 г.
^ Инчбальд, Гай (июль 1997 г.), «Архимедовы сотовые двойственные числа» , The Mathematical Gazette , 81 (491): 213–219, doi : 10.2307/3619198 , JSTOR 3619198 .

Дальнейшее чтение

Коксетер, HSM : Правильные многогранники .
Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc., стр. 164–199. ISBN 0-486-23729-Х . Глава 5: Упаковка многогранников и заполнение пространства
Кричлоу, К.: Порядок в космосе .
Пирс П.: Структура в природе — это стратегия дизайна .
Гольдберг, Майкл Три бесконечных семейства тетраэдрических заполнителей пространства Журнал комбинаторной теории A, 16, стр. 348–354, 1974.
Гольдберг, Майкл (1972). «Пятигранники, заполняющие пространство». Журнал комбинаторной теории, серия А. 13 (3): 437–443. дои : 10.1016/0097-3165(72)90077-5 .
Гольдберг, Майкл Пентаэдры, заполняющие пространство II , Журнал комбинаторной теории 17 (1974), 375–378.
Гольдберг, Майкл (1977). «О заполняющих пространство шестигранниках». Геометрии посвященные . 6 . дои : 10.1007/BF00181585 . S2CID 189889869 .
Гольдберг, Майкл (1978). «О заполняющих пространство семигранниках». Геометрии посвященные . 7 (2): 175–184. дои : 10.1007/BF00181630 . S2CID 120562040 .
Гольдберг, Майкл Выпуклые многогранные заполнители пространства с более чем двенадцатью гранями. Геом. Посвящение 8, 491–500, 1979.
Гольдберг, Майкл (1981). «О заполняющих пространство октаэдрах» . Геометрии посвященные . 10 (1–4): 323–335. дои : 10.1007/BF01447431 . S2CID 189876836 .
Гольдберг, Майкл (1982). «О заполняющих пространство декаэдрах». Структурная топология (7): 39–44. HDL : 2099/990 .
Гольдберг, Майкл (1982). «Об эннеаэдрах, заполняющих пространство». Геометрии посвященные . 12 (3). дои : 10.1007/BF00147314 . S2CID 120914105 .

Внешние ссылки

Ольшевский, Георгий. «Соты» . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года.
Пять заполняющих пространство многогранников , Гай Инчбальд, The Mathematical Gazette 80 , ноябрь 1996 г., стр. 466-475.
Раумфуллерлер (Многогранники, заполняющие пространство) Т. Е. Дорозинского
Вайсштейн, Эрик В. «Многогранник, заполняющий пространство» . Математический мир .

v т и Основные выпуклые правильные и однородные соты размеров 2–9.
Космос	Семья	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
И ²	Равномерная укладка плитки	{3 ^[3]}	д ₃	HD ₃	квартал ₃	Шестиугольный
И ³	Равномерные выпуклые соты	{3 ^[4]}	д ₄	HD ₄	4 _{квартала}
И ⁴	Униформа 4-сотовая	{3 ^[5]}	д ₅	hδ ₅	qδ ₅	24-ячеистые соты
И ⁵	Униформа 5-сотовая	{3 ^[6]}	д ₆	HD ₆	qδ ₆
И ⁶	Униформа 6-сотовая	{3 ^[7]}	д ₇	hδ ₇	qδ ₇	2 ₂₂
И ⁷	Униформа 7-сотовая	{3 ^[8]}	д ₈	hδ ₈	8 _{кварталов}	1 ₃₃ • 3 ₃₁
И ⁸	Униформа 8-сотовая	{3 ^[9]}	д ₉	HD ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
И ⁹	Униформа 9-сотовая	{3 ^[10]}	д ₁₀	HD ₁₀	10 _{кварталов}
И ¹⁰	Униформа 10-сотовая	{3 ^[11]}	д ₁₁	HD ₁₁	qδ ₁₁
И ^{п -1}	Равномерный ( n -1)- сотовый	{3 ^[н]}	δ _н	hδ _н	qδ _н	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁

[1] Грюнбаум (1994). «Равномерные замощения трехмерного пространства». Геомбинаторика 4(2)

[2] Вайсштейн, Эрик В. «Многогранник, заполняющий пространство» . Математический мир .

[3] Дебруннер, Ханс Э. (1980), «О равенстве разложения многогранников тротуара с кубами», Archives of Mathematics (на немецком языке), 35 (6): 583–587, doi : 10.1007/BF01235384 , MR 0604258 , S2CID 121301319 .

[4] Лагариас, JC ; Моьюс, Д. (1995), «Многогранники, заполняющие $\mathbb {R} ^{n}$ и конгруэнтность ножниц», «Дискретная и вычислительная геометрия» , 13 (3–4): 573–583, doi : 10.1007/BF02574064 , MR 1318797 .

[5] [1] Равномерное заполнение пространства с использованием треугольных, квадратных и шестиугольных призм.

[6] [2] Равномерное заполнение пространства с использованием только ромбо-шестиугольных додекаэдров.

[7] [3] Равномерное заполнение пространства с использованием только усеченных октаэдров.

[8] Джон Конвей (22 декабря 2003 г.). "Многогранник Вороного. геометрия.пазлы" . Группа новостей : geometry.puzzles . Usenet: Pine.LNX.4.44.0312221226380.25139-100000@fine318a.math.Princeton.EDU .

[9] X. Цянь, Д. Страс и Т. Шлик, J. Comput. хим. 22 (15) 1843–1850 (2001)

[10] [4] О. Дельгадо-Фридрихс и М. О'Киф. Изоэдральные простые замощения: бинодали и плитки с <16 гранями. Акта Кристаллогр. (2005) А61, 358-362

[11] [5] Архивировано 30 июня 2015 г. в Wayback Machine Gabbrielli, Руджеро. Тринадцатигранный многогранник, заполняющий пространство своей киральной копией.

[12] Полинг, Лайнус. Природа химической связи. Издательство Корнелльского университета, 1960 г.

[13] Инчбальд, Гай (июль 1997 г.), «Архимедовы сотовые двойственные числа» , The Mathematical Gazette , 81 (491): 213–219, doi : 10.2307/3619198 , JSTOR 3619198 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]