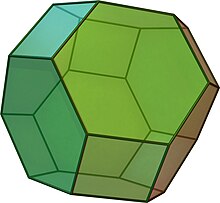
Усеченный октаэдр

Усеченный октаэдрический граф
Усеченный октаэдрический граф
	Трехкратная симметричная диаграмма Шлегеля
Вершины	24
Края	36
Автоморфизмы	48
Хроматическое число	2
Толщина книги	3
Номер очереди	2
Характеристики	Кубический , гамильтонов , регулярный , нуль-симметричный
	Таблица графиков и параметров

Усеченный октаэдр
Усеченный октаэдр
Тип	Архимедово тело , ; Параллелоэдр , ; Пермутоэдр , ; плесоэдр , ; Зоноэдр
Лица	14
Края	36
Вершины	24
Группа симметрии	октаэдрическая симметрия
Двойной многогранник	тетракис шестигранник
Вершинная фигура
Сеть

В геометрии — усеченный октаэдр это архимедово тело , которое получается из правильного октаэдра путем удаления шести пирамид, по одной в каждой вершине октаэдра. Усеченный октаэдр имеет 14 граней (8 правильных шестиугольников и 6 квадратов ), 36 ребер и 24 вершины. Поскольку каждая его грань имеет точечную симметрию, усечённый октаэдр является 6 - зоноэдром . Это также многогранник Гольдберга G _IV (1,1), содержащий квадратные и шестиугольные грани. Как и куб, он может замощить (или «упаковать») трехмерное пространство, как пермутоэдр .

назвал «меконом» Усеченный октаэдр Бакминстер Фуллер . ^[1]

Его двойственный многогранник — тетракис-шестигранник . Если исходный усеченный октаэдр имеет единичную длину ребра, его двойной тетракис-гексаэдр имеет длину ребра. ⁠ 9/8 ⁠ √ 2 и ⁠ 3 / 2 ⁠ √ 2 .

Классификации

Как архимедово тело

Усечённый октаэдр получается из правильного октаэдра путём отсечения всех вершин. В результате получается многогранник, состоящий из шести квадратов и восьми шестиугольников, исключая шесть квадратных пирамид . Учитывая, что каждая длина правильного октаэдра равна $3a$ , а длина ребра квадратной пирамиды равна $a$ (квадратная пирамида — равносторонняя , первое тело Джонсона ). Из свойства равносторонней квадратной пирамиды ее объем равен ${\textstyle {\tfrac {\sqrt {2}}{6}}a^{3}}$ . Поскольку шесть равносторонних квадратных пирамид удаляются путем усечения, объем усеченного октаэдра $V$ получается вычитанием объема правильного октаэдра из этих шести: ^[2] $V={\frac {\sqrt {2}}{3}}(3a)^{3}-6\cdot {\frac {\sqrt {2}}{6}}a^{3}=8a^{3}{\sqrt {2}}\approx 11.3137.$ Площадь поверхности усеченного октаэдра можно получить, суммируя площади всех многоугольников, шести квадратов и восьми шестиугольников. Учитывая длину ребра $a$ , Это: ^[2] $(6+12{\sqrt {3}})a^{2}\approx 26.7846a^{2}.$

Усечённый октаэдр — одно из тринадцати архимедовых тел . Другими словами, он имеет высокосимметричный и полуправильный многогранник с двумя или более разными правильными многоугольными гранями, сходящимися в вершине. ^[3] Двойной многогранник усеченного октаэдра — тетракис-гексаэдр . Оба они имеют ту же трехмерную группу симметрии, что и правильный октаэдр, — октаэдрическую симметрию. $\mathrm {O} _{\mathrm {h} }$ . ^[4] Каждую его вершину окружают квадрат и два шестиугольника, обозначая фигуру вершины как $4\cdot 6^{2}$ . ^[5]

Двугранный угол усеченного октаэдра между квадратом и шестиугольником равен ${\textstyle \arccos(-1/{\sqrt {3}})\approx 125.26^{\circ }}$ , а между соседними шестиугольными гранями ${\textstyle \arccos(-1/3)\approx 109.47^{\circ }}$ . ^[6]

Как обрабатываемый пространственный многогранник

Усеченный октаэдр как пермутаэдр четвертого порядка.

Усеченный октаэдр в обрабатываемом пространстве

Усеченный октаэдр можно описать как пермутоэдр 4-го порядка или 4-пермутоэдр , то есть его можно представить с еще более симметричными координатами в четырех измерениях: все перестановки $(1,2,3,4)$ образуют вершины усеченного октаэдра в трехмерном подпространстве $x+y+z+w=10$ . ^[7] Таким образом, каждая вершина соответствует перестановке $(1,2,3,4)$ и каждое ребро представляет собой одну попарную замену двух элементов. Имеет симметричную группу $S_{4}$ . ^[8]

Усеченный октаэдр можно использовать как пространство для обработки почвы. Он классифицируется как плезиоэдр , то есть его можно определить как ячейку Вороного симметричного множества Делоне . ^[9] В состав плезиоэдра входит параллелоэдр , многогранник можно перемещать, не вращая и обрабатывая пространство так, что он заполняет всю грань. Существует пять трехмерных первичных параллелоэдров, один из которых — усеченный октаэдр. ^[10] В более общем смысле, каждый пермутоэдр и параллелоэдр представляет собой зоноэдр многогранник , центрально-симметричный , который можно определить с помощью суммы Минковского . ^[11]

Как многогранник Гольдберга

Усеченный октаэдр — это многогранник Гольдберга , многогранник с шестиугольными или пятиугольными гранями. ^[12]

Приложения

Строение фожазитового каркаса

Первая зона Бриллюэна решетки FCC с метками симметрии для линий и точек высокой симметрии.

В химии усеченный октаэдр представляет собой каркасную структуру содалита в каркасе фожазита типа кристаллов цеолита . ^[13]

В физике твердого тела первая зона Бриллюэна гранецентрированной кубической решетки представляет собой усеченный октаэдр. ^[14]

Усеченный октаэдр (фактически обобщенный усеченный октаэдр) появляется при анализе ошибок модуляции индекса квантования (QIM) в сочетании с повторным кодированием. ^[15]

Диссекция

Усеченный октаэдр можно разрезать на центральный октаэдр , окруженный 8 треугольными куполами на каждой грани и 6 квадратными пирамидами над вершинами. ^[16]

Удаление центрального октаэдра и 2 или 4 треугольных куполов создает два тороида Стюарта с двугранной и тетраэдрической симметрией:

Род 2	Род 3
Д _3д , [2 ⁺,6], (2*3), порядок 12	T _d , [3,3], (*332), порядок 24

можно разрезать Тессеракт гиперплоскостью так, чтобы его поперечное сечение представляло собой усеченный октаэдр. ^[17]

Ячеисто -транзитивные побитовые кубические соты также можно рассматривать как мозаику Вороного объемноцентрированной кубической решетки . Усечённый октаэдр — один из пяти трёхмерных первичных параллелоэдров .

Объекты

Сетки для занятий джунглями часто включают в себя усеченные октаэдры.

древние китайцы умирают
скульптура в Бонне
кубика Рубика Вариант
Модель сделана с помощью конструктора Полидрон.
пирита Кристалл
болеита Кристалл

Усеченный октаэдрический граф

В математической области теории графов усеченный октаэдрический граф — это граф вершин и ребер усеченного октаэдра. Он имеет 24 вершины и 36 ребер и представляет собой кубический архимедовый граф . ^[18] Имеет толщину книги 3 и номер очереди 2. ^[19]

Как гамильтонов кубический граф , его можно представить в обозначениях LCF несколькими способами: [3, −7, 7, −3] ⁶, [5, −11, 11, 7, 5, −5, −7, −11, 11, −5, −7, 7] ², и [−11, 5, −3, −7, −9, 3, −5, 5, −3, 9, 7, 3, −5, 11, −3, 7, 5, −7, −9 , 9, 7, −5, −7, 3]. ^[20]

Ссылки

^ «Усечённый октаэдр» . Вольфрам Математический мир .
^ Перейти обратно: ^а ^б Берман, Мартин (1971). «Выпуклые многогранники с правильными гранями». Журнал Института Франклина . 291 (5): 329–352. дои : 10.1016/0016-0032(71)90071-8 . МР 0290245 .
^ Дюдя, МВ (2018). Многооболочечные многогранные кластеры . Спрингер . п. 39. дои : 10.1007/978-3-319-64123-2 . ISBN 978-3-319-64123-2 .
^ Коджа, М.; Коджа, НЕТ (2013). «Группы Кокстера, кватернионы, симметрии многогранников и 4D-многогранники» . Математическая физика: материалы 13-й региональной конференции, Анталья, Турция, 27–31 октября 2010 г. Всемирная научная. п. 48.
^ Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. с. 78.
^ Джонсон, Норман В. (1966). «Выпуклые многогранники с правильными гранями» . Канадский математический журнал . 18 : 169–200. дои : 10.4153/cjm-1966-021-8 . МР 0185507 . S2CID 122006114 . Збл 0132.14603 .
^ Джонсон, Том; Енджеевский, Франк (2014). Глядя на цифры . Спрингер. п. 15. дои : 10.1007/978-3-0348-0554-4 . ISBN 978-3-0348-0554-4 .
^ Крисман, Карл-Дитер (2011). «Группа симметрии пермутаэдра». Математический журнал колледжа . 42 (2): 135–139. дои : 10.4169/college.math.j.42.2.135 . JSTOR College.math.j.42.2.135 .
^ Эрдал, РМ (1999). «Зонотопы, игральные кости и гипотеза Вороного о параллелоэдрах» . Европейский журнал комбинаторики . 20 (6): 527–549. дои : 10.1006/eujc.1999.0294 . МР 1703597 . . Вороной предположил, что все разбиения пространств более высоких размерностей сдвигами одного выпуклого многогранника комбинаторно эквивалентны разбиениям Вороного, и Эрдал доказывает это в частном случае зонотопов . Но, как он пишет (стр. 429), гипотеза Вороного для размерностей не более четырех была доказана уже Делоне. О классификации трехмерных параллелоэдров на эти пять типов см. Грюнбаум, Бранко ; Шепард, GC (1980). «Плитки с одинаковыми плитками» . Бюллетень Американского математического общества . Новая серия. 3 (3): 951–973. дои : 10.1090/S0273-0979-1980-14827-2 . МР 0585178 .
^ Александров, А.Д. (2005). «8.1 Параллелоэдры» . Выпуклые многогранники . Спрингер. стр. 349–359.
^ Дженсен, Патрик М.; Триндерап, Камилия Х.; Даль, Андерс Б.; Даль, Ведрана А. (2019). «Зоноэдральная аппроксимация сферического структурирующего элемента для объемной морфологии» . В Фельсберге, Майкл; Форссен, Пер-Эрик; Синторн, Ида-Мария; Унгер, Йонас (ред.). Анализ изображений: 21-я Скандинавская конференция, SCIA 2019, Норчёпинг, Швеция, 11–13 июня 2019 г., Материалы . Спрингер. п. 131–132. дои : 10.1007/978-3-030-20205-7 . ISBN 978-3-030-20205-7 .
^ Шейн, С.; Гайед, Дж. М. (2014). «Четвертый класс выпуклых равносторонних многогранников с полиэдрической симметрией, родственный фуллеренам и вирусам» . Труды Национальной академии наук . 111 (8): 2920–2925. Бибкод : 2014PNAS..111.2920S . дои : 10.1073/pnas.1310939111 . ISSN 0027-8424 . ПМЦ 3939887 . ПМИД 24516137 .
^ Йен, Тех Ф. (2007). Химические процессы в экологической инженерии . Издательство Имперского колледжа. п. 338. ИСБН 978-1-86094-759-9 .
^ Мизутани, Уитиро (2001). Введение в электронную теорию металлов . Издательство Кембриджского университета . п. 112.
^ Перес-Гонсалес, Ф.; Баладо, Ф.; Мартин, JRH (2003). «Анализ производительности существующих и новых методов сокрытия данных с информацией об известном хосте в аддитивных каналах». Транзакции IEEE по обработке сигналов . 51 (4): 960–980. Бибкод : 2003ИТСП...51..960П . дои : 10.1109/TSP.2003.809368 .
^ Доски, Алекс. «Приключения среди тороидов - Глава 5 - Простейшие (R) (A) (Q) (T) тороиды рода p = 1» . www.doskey.com .
^ Боровик, Александр Владимирович; Боровик, Анна (2010), «Упражнение 14.4» , Зеркала и отражения , Universitext, Нью-Йорк: Springer, с. 109, номер домена : 10.1007/978-0-387-79066-4 , ISBN 978-0-387-79065-7 , МР 2561378
^ Читай, RC; Уилсон, Р.Дж. (1998), Атлас графиков , Oxford University Press , стр. 269
^ Вольц, Джессика; Проектирование линейных макетов с помощью SAT. Магистерская диссертация, Тюбингенский университет, 2018 г.
^ Вайсштейн, Эрик В. «Усеченный октаэдрический граф» . Математический мир .

Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN 0-486-23729-Х . (Раздел 3–9)
Фрейтас, Роберт А. младший (1999). «Рисунок 5.5: Равномерное заполнение пространства с использованием только усеченных октаэдров» . Наномедицина, Том I: Основные возможности . Джорджтаун, Техас: Landes Bioscience . Проверено 8 сентября 2006 г.
Гаиха П. и Гуха С.К. (1977). «Смежные вершины пермутоэдра». SIAM Journal по прикладной математике . 32 (2): 323–327. дои : 10.1137/0132025 .
Харт, Джордж В. «VRML-модель усеченного октаэдра» . Виртуальные многогранники: Энциклопедия многогранников . Проверено 8 сентября 2006 г.
Мэдер, Роман. «Однородные многогранники: усечённый октаэдр» . Проверено 8 сентября 2006 г.
Александров, А.Д. (1958). Выпуклый многогранник . Берлин: Шпрингер. стр. 539. ИСБН 3-540-23158-7 .
Кромвель, П. (1997). Многогранники . Великобритания: Кембридж. С. 79–86 Архимедовы тела . ISBN 0-521-55432-2 .

Внешние ссылки

[1] «Усечённый октаэдр» . Вольфрам Математический мир .

[berman-2] Перейти обратно: ^а ^б Берман, Мартин (1971). «Выпуклые многогранники с правильными гранями». Журнал Института Франклина . 291 (5): 329–352. дои : 10.1016/0016-0032(71)90071-8 . МР 0290245 .

[diudea-3] Дюдя, МВ (2018). Многооболочечные многогранные кластеры . Спрингер . п. 39. дои : 10.1007/978-3-319-64123-2 . ISBN 978-3-319-64123-2 .

[kocakoca-4] Коджа, М.; Коджа, НЕТ (2013). «Группы Кокстера, кватернионы, симметрии многогранников и 4D-многогранники» . Математическая физика: материалы 13-й региональной конференции, Анталья, Турция, 27–31 октября 2010 г. Всемирная научная. п. 48.

[williams-5] Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. с. 78.

[johnson-6] Джонсон, Норман В. (1966). «Выпуклые многогранники с правильными гранями» . Канадский математический журнал . 18 : 169–200. дои : 10.4153/cjm-1966-021-8 . МР 0185507 . S2CID 122006114 . Збл 0132.14603 .

[jj-7] Джонсон, Том; Енджеевский, Франк (2014). Глядя на цифры . Спрингер. п. 15. дои : 10.1007/978-3-0348-0554-4 . ISBN 978-3-0348-0554-4 .

[crisman-8] Крисман, Карл-Дитер (2011). «Группа симметрии пермутаэдра». Математический журнал колледжа . 42 (2): 135–139. дои : 10.4169/college.math.j.42.2.135 . JSTOR College.math.j.42.2.135 .

[erdahl-9] Эрдал, РМ (1999). «Зонотопы, игральные кости и гипотеза Вороного о параллелоэдрах» . Европейский журнал комбинаторики . 20 (6): 527–549. дои : 10.1006/eujc.1999.0294 . МР 1703597 . . Вороной предположил, что все разбиения пространств более высоких размерностей сдвигами одного выпуклого многогранника комбинаторно эквивалентны разбиениям Вороного, и Эрдал доказывает это в частном случае зонотопов . Но, как он пишет (стр. 429), гипотеза Вороного для размерностей не более четырех была доказана уже Делоне. О классификации трехмерных параллелоэдров на эти пять типов см. Грюнбаум, Бранко ; Шепард, GC (1980). «Плитки с одинаковыми плитками» . Бюллетень Американского математического общества . Новая серия. 3 (3): 951–973. дои : 10.1090/S0273-0979-1980-14827-2 . МР 0585178 .

[alexandrov-10] Александров, А.Д. (2005). «8.1 Параллелоэдры» . Выпуклые многогранники . Спрингер. стр. 349–359.

[jtdd-11] Дженсен, Патрик М.; Триндерап, Камилия Х.; Даль, Андерс Б.; Даль, Ведрана А. (2019). «Зоноэдральная аппроксимация сферического структурирующего элемента для объемной морфологии» . В Фельсберге, Майкл; Форссен, Пер-Эрик; Синторн, Ида-Мария; Унгер, Йонас (ред.). Анализ изображений: 21-я Скандинавская конференция, SCIA 2019, Норчёпинг, Швеция, 11–13 июня 2019 г., Материалы . Спрингер. п. 131–132. дои : 10.1007/978-3-030-20205-7 . ISBN 978-3-030-20205-7 .

[sg-12] Шейн, С.; Гайед, Дж. М. (2014). «Четвертый класс выпуклых равносторонних многогранников с полиэдрической симметрией, родственный фуллеренам и вирусам» . Труды Национальной академии наук . 111 (8): 2920–2925. Бибкод : 2014PNAS..111.2920S . дои : 10.1073/pnas.1310939111 . ISSN 0027-8424 . ПМЦ 3939887 . ПМИД 24516137 .

[yen-13] Йен, Тех Ф. (2007). Химические процессы в экологической инженерии . Издательство Имперского колледжа. п. 338. ИСБН 978-1-86094-759-9 .

[mizutani-14] Мизутани, Уитиро (2001). Введение в электронную теорию металлов . Издательство Кембриджского университета . п. 112.

[15] Перес-Гонсалес, Ф.; Баладо, Ф.; Мартин, JRH (2003). «Анализ производительности существующих и новых методов сокрытия данных с информацией об известном хосте в аддитивных каналах». Транзакции IEEE по обработке сигналов . 51 (4): 960–980. Бибкод : 2003ИТСП...51..960П . дои : 10.1109/TSP.2003.809368 .

[16] Доски, Алекс. «Приключения среди тороидов - Глава 5 - Простейшие (R) (A) (Q) (T) тороиды рода p = 1» . www.doskey.com .

[17] Боровик, Александр Владимирович; Боровик, Анна (2010), «Упражнение 14.4» , Зеркала и отражения , Universitext, Нью-Йорк: Springer, с. 109, номер домена : 10.1007/978-0-387-79066-4 , ISBN 978-0-387-79065-7 , МР 2561378

[18] Читай, RC; Уилсон, Р.Дж. (1998), Атлас графиков , Oxford University Press , стр. 269

[19] Вольц, Джессика; Проектирование линейных макетов с помощью SAT. Магистерская диссертация, Тюбингенский университет, 2018 г.

[20] Вайсштейн, Эрик В. «Усеченный октаэдрический граф» . Математический мир .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]