Разрезанные кубические соты

Разрезанные кубические соты

Тип	Равномерные соты
Символ Шлефли	2т{4,3,4} т _1,2 {4,3,4}
Диаграмма Кокстера-Динкина
Тип ячейки	( 4.6.6 )
Типы лица	квадрат {4} шестигранник {6}
Краевая фигура	равнобедренный треугольник {3}
Вершинная фигура	( тетрагональный дисфеноид )
Космическая группа Обозначение фиброфолда Обозначение Кокстера	Мне 3 метра (229) 8 ^тот:2 [[4,3,4]]
Группа Коксетера	${\tilde {C}}_{3}$ , [4,3,4]
Двойной	Сплюснутый тетраэдрилл Дисфеноидные тетраэдрические соты Клетка:
Характеристики	изогональный , изотоксальный , изохорный

Битусеченные кубические соты — это заполняющая пространство мозаика (или соты ) в евклидовом трехмерном пространстве, состоящая из усеченных октаэдров (или, что то же самое, усеченных кубов). Вокруг каждой вершины имеется 4 усеченных октаэдра. Будучи полностью состоящим из усеченных октаэдров , он является клеточно-транзитивным . Он также транзитивен по ребрам , с двумя шестиугольниками и одним квадратом на каждом ребре, и транзитивен по вершинам . Это одна из 28 единых сот .

Джон Хортон Конвей называет эту соту усеченным октаэдрилом в своем списке архитектонической и катоптрической мозаики , а ее двойник называется сплюснутым тетраэдрилом , также называемым дисфеноидным тетраэдрическим сотом . Хотя правильный тетраэдр не может сам по себе мозаику, этот двойственный тетраэдр имеет идентичные ячейки дисфеноидного тетраэдра с гранями равнобедренного треугольника .

Геометрия

Ее можно реализовать как мозаику Вороного объемноцентрированной кубической решетки. Лорд Кельвин предположил, что вариант усеченных кубических сот (с изогнутыми гранями и краями, но с той же комбинаторной структурой) является оптимальной пеной для мыльных пузырей. Однако позже было обнаружено, что ряд менее симметричных структур представляют собой более эффективные пены из мыльных пузырей, среди которых структура Вейра-Фелана оказалась лучшей.

Соты представляют собой мозаику пермутоэдров для трехмерного пространства. Координаты вершин одного октаэдра представляют собой гиперплоскость целых чисел в 4-мерном пространстве, а именно перестановки (1,2,3,4). Тесселяция формируется транслируемыми копиями внутри гиперплоскости.

Тесселяция — это высшая мозаика параллелоэдров в трехмерном пространстве.

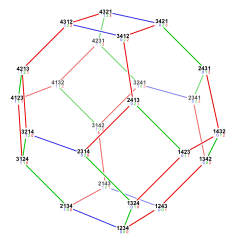
Прогнозы

Кубические соты с усеченными кусочками можно ортогонально спроецировать на евклидову плоскость с различными вариантами симметрии. Форма высшей (шестиугольной) симметрии образует неоднородную ромботригексагональную мозаику . Проекция квадратной симметрии образует две перекрывающиеся усеченные квадратные мозаики , которые объединяются вместе в квадратную мозаику со скошенными краями .

Ортогональные проекции
Симметрия	п6м (*632)	п4м (*442)	пмм (*2222)
Твердый
Рамка

Симметрия

Вершинной фигурой этой соты является дисфеноидный тетраэдр , а также тетраэдр Гурса ( фундаментальная область ) для ${\tilde {A}}_{3}$ Группа Кокстера . Эти соты имеют четыре однородные конструкции, причем усеченные октаэдрические ячейки имеют разные группы Кокстера и конструкции Витхоффа . Эти однородные симметрии можно представить, раскрасив по-разному ячейки в каждой конструкции.

Пять однородных раскрасок по клеточкам
Космическая группа	Мне 3 метра (229)	ПМ 3 м (221)	Фм 3 м (225)	Ф 4 3м (216)	Фд 3м (227)
Фибрифолд	8 ^тот:2	4 ⁻:2	2 ⁻:2	1 ^тот:2	2 ⁺:2
Группа Коксетера	${\tilde {C}}_{3}$ ×2 [[4,3,4]] =[4[3 ^[4]]] =	${\tilde {C}}_{3}$ [4,3,4] =[2[3 ^[4]]] =	${\tilde {B}}_{3}$ [4,3 ^1,1] =<[3 ^[4]]> =	${\tilde {A}}_{3}$ [3 ^[4]]	${\tilde {A}}_{3}$ ×2 [[3 ^[4]]] =[[3 ^[4]]]
Диаграмма Кокстера
усеченные октаэдры	1	1:1 :	2:1:1 : :	1:1:1:1 : : :	1:1 :
Вершинная фигура
Вертекс фигура симметрия	[2 ⁺,4] (заказ 8)	[2] (заказ 4)	[ ] (заказ 2)	[ ] ⁺ (заказ 1)	[2] ⁺ (заказ 2)
Изображение Раскрашено клетка

Связанные многогранники и соты

Правильный косой апейроэдр {6,4|4} содержит шестиугольники этих сот.

[4,3,4], генерирует Группа Коксетера 15 перестановок однородных мозаик, 9 из которых имеют четкую геометрию, включая чередующиеся кубические соты. Расширенные кубические соты (также известные как сморщенные тессерактические соты) геометрически идентичны кубическим сотам.

Соты C3
Space group	Fibrifold	Extended symmetry	Extended diagram	Order	Honeycombs
Pm3m (221)	4⁻:2	[4,3,4]		×1	₁, ₂, ₃, ₄, ₅, ₆
Fm3m (225)	2⁻:2	[1⁺,4,3,4] ↔ [4,3^1,1]	↔	Half	₇, ₁₁, ₁₂, ₁₃
I43m (217)	4^o:2	[[(4,3,4,2⁺)]]		Half × 2	₍₇₎,
Fd3m (227)	2⁺:2	[[1⁺,4,3,4,1⁺]] ↔ [[3^[4]]]	↔	Quarter × 2	₁₀,
Im3m (229)	8^o:2	[[4,3,4]]		×2	₍₁₎, ₈, ₉

[4,3 ^1,1], генерирует Группа Коксетера 9 перестановок однородных мозаик, 4 из которых имеют четкую геометрию, включая чередующиеся кубические соты.

Соты B3
Space group	Fibrifold	Extended symmetry	Extended diagram	Order	Honeycombs
Fm3m (225)	2⁻:2	[4,3^1,1] ↔ [4,3,4,1⁺]	↔	×1	₁, ₂, ₃, ₄
Fm3m (225)	2⁻:2	<[1⁺,4,3^1,1]> ↔ <[3^[4]]>	↔	×2	₍₁₎, ₍₃₎
Pm3m (221)	4⁻:2	<[4,3^1,1]>		×2	₅, ₆, ₇, ₍₆₎, ₉, ₁₀, ₁₁

Эти соты являются одними из пяти различных однородных сот. ^[1] построенный ${\tilde {A}}_{3}$ Группа Кокстера . Симметрию можно помножить на симметрию колец в диаграммах Кокстера – Дынкина :

Соты А3
Space group	Fibrifold	Square symmetry	Extended symmetry	Extended diagram	Extended group	Honeycomb diagrams
F43m (216)	1^o:2	a1	[3^[4]]		${\tilde {A}}_{3}$	(None)
Fm3m (225)	2⁻:2	d2	<[3^[4]]> ↔ [4,3^1,1]	↔	${\tilde {A}}_{3}$ ×2₁ ↔ ${\tilde {B}}_{3}$	₁, ₂
Fd3m (227)	2⁺:2	g2	[[3^[4]]] or [2⁺[3^[4]]]	↔	${\tilde {A}}_{3}$ ×2₂	₃
Pm3m (221)	4⁻:2	d4	<2[3^[4]]> ↔ [4,3,4]	↔	${\tilde {A}}_{3}$ ×4₁ ↔ ${\tilde {C}}_{3}$	₄
I3 (204)	8^−o	r8	[4[3^[4]]]⁺ ↔ [[4,3⁺,4]]	↔	½ ${\tilde {A}}_{3}$ ×8 ↔ ½ ${\tilde {C}}_{3}$ ×2	_(*)
Im3m (229)	8^o:2	r8	[4[3^[4]]] ↔ [[4,3,4]]	↔	${\tilde {A}}_{3}$ ×8 ↔ ${\tilde {C}}_{3}$ ×2	₅

Альтернативная форма

Чередованные битусеченные кубические соты
Тип	Выпуклые соты
Символ Шлефли	2с{4,3,4} 2с{4,3 ^1,1} ср{3 ^[4]}
Диаграммы Кокстера	= = =
Клетки	тетраэдр икосаэдр
Вершинная фигура
Группа Коксетера	[[4,3 ⁺,4]], ${\tilde {C}}_{3}$
Двойной	Соты из десяти бубнов Клетка:
Характеристики	вершинно-транзитивный

Эти соты можно чередовать , создавая из усеченных октаэдров пиритоэдрические икосаэдры с созданными в промежутках дисфеноидными тетраэдрическими ячейками. Есть три конструкции из трех связанных диаграмм Кокстера-Динкина : , , и . Они обладают симметрией [4,3 ⁺,4], [4,(3 ^1,1) ⁺] и [3 ^[4]] ⁺ соответственно. Первую и последнюю симметрию можно удвоить как [[4,3 ⁺,4]] и [[3 ^[4]]] ⁺.

Двойные соты состоят из ячеек, называемых десятигранниками .

Пять однородных раскрасок
Космическая группа	Я 3 (204)	Вечер 3 (200)	Фм 3 (202)	Фд 3 (203)	Ф23 (196)
Фибрифолд	8 ^−о	4 ⁻	2 ⁻	2 ^о+	1 ^тот
Группа Коксетера	[[4,3 ⁺,4]]	[4,3 ⁺,4]	[4,(3 ^1,1) ⁺]	[[3 ^[4]]] ⁺	[3 ^[4]] ⁺
Диаграмма Кокстера
Заказ	двойной	полный	половина	четверть двойной	четверть
Изображение окрашенный по клеткам

Эти соты представлены атомами бора α-ромбоэдрического кристалла . Центры икосаэдров расположены в ГЦК-положениях решетки. ^[2]

Связанные многогранники

Неоднородные варианты с симметрией [4,3,4] и двумя типами усеченных октаэдров можно удвоить, поместив два типа усеченных октаэдров для получения неоднородной соты с усеченными октаэдрами и шестиугольными призмами (как дитригональные трапезопризмы). Ее вершинной фигурой является C _2v -симметричная треугольная бипирамида .

Затем эти соты можно чередовать, чтобы получить еще одну неоднородную соту с пиритоэдрическими икосаэдрами , октаэдрами (как треугольные антипризмы) и тетраэдрами (как клиновидные). Его вершинная фигура имеет симметрию C _2v и состоит из 2 пятиугольников , 4 прямоугольников , 4 равнобедренных треугольников (разделенных на два набора по 2) и 4 разносторонних треугольников .

См. также

Примечания

^ [1] , A000029 6-1 случаев, пропуск одного с нулевыми оценками
^ Уильямс, 1979, стр. 199, рисунок 5-38.

Ссылки

Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус , (2008) Симметрии вещей , ISBN 978-1-56881-220-5 (Глава 21, Наименование архимедовых и каталонских многогранников и мозаик, Архитектурные и катоптрические мозаики, стр. 292-298, включает все непризматические формы)
Георгий Ольшевский, Равномерные паноплоидные тетракомбы , Рукопись (2006) (Полный список из 11 выпуклых однородных мозаик, 28 выпуклых однородных сот и 143 выпуклых однородных тетракомб)
Бранко Грюнбаум , Равномерные разбиения трехмерного пространства. Геомбинаторика 4 (1994), 49–56.
Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10] (1.9 Равномерные пространственные заполнения)
А. Андреини , О правильных и полуправильных сетях многогранников и о соответствующих корреляционных сетях , Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
Клитцинг, Ричард. «3D Евклидовы соты o4x3x4o — пакет — O16» .
Однородные соты в 3-пространстве: 05-Batch
Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN 0-486-23729-Х .

Внешние ссылки

Вайсштейн, Эрик В. «Многогранник, заполняющий пространство» . Математический мир .

[1] [1] , A000029 6-1 случаев, пропуск одного с нулевыми оценками

[2] Уильямс, 1979, стр. 199, рисунок 5-38.

[1]

[2]