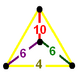
Тетраэдр Гурса
В геометрии — тетраэдр Гурса это тетраэдрическая фундаментальная область конструкции Витгофа . Каждая тетраэдрическая грань представляет собой гиперплоскость отражения на трехмерных поверхностях: трехмерной сфере , евклидовом трехмерном пространстве и гиперболическом трехмерном пространстве. Коксетер назвал их в честь Эдуарда Гурса , который первым изучил эти области. Это расширение теории треугольников Шварца для конструкций Витгофа на сфере.
Графическое представление
[ редактировать ]Тетраэдр Гурса можно графически представить в виде тетраэдрического графа, который находится в двойной конфигурации тетраэдра фундаментальной области. В графе каждый узел представляет собой грань (зеркало) тетраэдра Гурса. Каждое ребро помечено рациональным значением, соответствующим порядку отражения, которое равно π/ двугранному углу .
с 4 узлами Диаграмма Коксетера-Динкина представляет этот тетраэдрический граф со скрытыми ребрами второго порядка. Если многие ребра имеют порядок 2, группу Кокстера можно представить с помощью скобок .
Для существования требуется, чтобы каждый из 3-узловых подграфов этого графа (pqr), (pus), (qtu) и (rst) соответствовал треугольнику Шварца .
Расширенная симметрия
[ редактировать ] |  |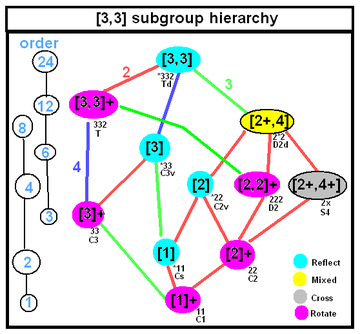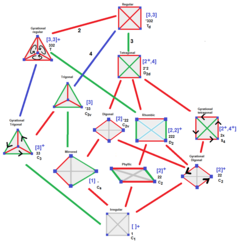
| Симметрия тетраэдра Гурса может быть тетраэдрической симметрией любой симметрии подгруппы, показанной в этом дереве, с подгруппами ниже с индексами подгрупп, отмеченными на цветных краях. | |
Расширенная симметрия тетраэдра Гурса является полупрямым произведением симметрии группы Коксетера и симметрии фундаментальной области (в этих случаях тетраэдра Гурса). Обозначение Кокстера поддерживает эту симметрию, поскольку двойные скобки, такие как [Y[X]] означают полную симметрию группы Кокстера [X], где Y является симметрией тетраэдра Гурса. Если Y представляет собой чистую отражательную симметрию, группа будет представлять собой другую группу зеркал Кокстера. Если существует только одна простая удвоенная симметрия, Y может быть неявным, как [[X]] с отражательной или вращательной симметрией в зависимости от контекста.
Расширенная симметрия каждого тетраэдра Гурса также приведена ниже. Наивысшая возможная симметрия - это симметрия правильного тетраэдра , как [3,3], и это происходит в призматической точечной группе [2,2,2] или [2 [3,3] ] и паракомпактная гиперболическая группа [3 [3,3] ].
См . Тетраэдр # Изометрии неправильных тетраэдров, чтобы узнать о семи изометриях нижней симметрии тетраэдра.
Целочисленные решения
[ редактировать ]В следующих разделах показаны все целочисленные тетраэдрические решения Гурса в трехмерной сфере, евклидовом трехмерном пространстве и гиперболическом трехмерном пространстве. Также дана расширенная симметрия каждого тетраэдра.
Цветные тетраэдрические диаграммы ниже представляют собой фигуры вершин всеусеченных многогранников и сот из каждого семейства симметрии. Метки ребер представляют порядок полигональных граней, что вдвое превышает порядок ветвей графа Коксетера. Двугранный угол ребра, обозначенного 2n, равен π/ n . Желтые ребра, помеченные цифрой 4, исходят из прямоугольных (несвязанных) зеркальных узлов на диаграмме Коксетера.
3-сферные (конечные) решения
[ редактировать ]
Решения для 3-сферы с плотностью 1: ( Равномерная полихора )
| Группа Коксетера и диаграмма | [2,2,2]   | [п,2,2]  | [п,2,д]  | [п,2,п] | [3,3,2]  | [4,3,2]  | [5,3,2]  |
|---|---|---|---|---|---|---|---|
| Порядок симметрии группы | 16 | 8 р. | 4 шт. | 4 р. 2 | 48 | 96 | 240 |
| Тетраэдр симметрия | [3,3] (заказ 24)  | [2] (заказ 4)  | [2] (заказ 4) | [2 + ,4] (заказ 8)  | [ ] (заказ 2)  | [ ] + (заказ 1)  | [ ] + (заказ 1) |
| Расширенная симметрия | [(3,3)[2,2,2]]  =[4,3,3] | [2[п,2,2]]  =[2p,2,4]  | [2[p,2,q]] =[2p,2,2q] | [(2 + ,4)[п,2,р]] =[2 + [2п,2,2п]] | [1[3,3,2]]  =[4,3,2] | [4,3,2]  | [5,3,2] |
| Расширенный порядок симметрии | 384 | 32 р. | 16 кв.м. | 32 р. 2 | 96 | 96 | 240 |
| Тип графика | Линейный | Трезубый | |||
|---|---|---|---|---|---|
| Группа Коксетера и диаграмма | Пентахорический [3,3,3] | гексадекахорный [4,3,3] | Икозитетрахорический [3,4,3] | гексакосихорий [5,3,3] | Демитэссерактический [3 1,1,1 ]   |
| Вершинная фигура всеусеченной однородной полихоры | |||||
| Тетраэдр |  |  |  |  |  |
| Порядок симметрии группы | 120 | 384 | 1152 | 14400 | 192 |
| Тетраэдр симметрия | [2] + (заказ 2)  | [ ] + (заказ 1) | [2] + (заказ 2) | [ ] + (заказ 1) | [3] (заказ 6)  |
| Расширенная симметрия | [2 + [3,3,3]]    | [4,3,3] | [2 + [3,4,3]]  | [5,3,3] | [3[3 1,1,1 ]]  =[3,4,3] |
| Расширенный порядок симметрии | 240 | 384 | 2304 | 14400 | 1152 |
Евклидовы (аффинные) трехмерные решения
[ редактировать ]
Решения с плотностью 1: Выпуклые однородные соты :
| Тип графика | Линейный Ортосхема | Трезубый Плагиосхема | Петля Циклосхема | Призматический | Выродиться | ||
|---|---|---|---|---|---|---|---|
| Группа Коксетера Диаграмма Кокстера | [4,3,4] | [4,3 1,1 ] | [3 [4] ]  | [4,4,2] | [6,3,2]  | [3 [3] ,2] | [∞,2,∞]  |
| Вершинная фигура всеусеченных сот | |||||||
| Тетраэдр |  |  |  | ||||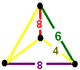
| Тетраэдр Симметрия | [2] + (заказ 2) | [ ] (заказ 2) | [2 + ,4] (заказ 8) | [ ] (заказ 2) | [ ] + (заказ 1) | [3] (заказ 6) | [2 + ,4] (заказ 8) |
| Расширенная симметрия | [(2 + )[4,3,4]]   | [1[4,3 1,1 ]] =[4,3,4] | [(2 + ,4)[3 [4] ]] =[2 + [4,3,4]] | [1[4,4,2]] =[4,4,2] | [6,3,2] | [3[3 [3] ,2]] =[3,6,2] | [(2 + ,4)[∞,2,∞]] =[1[4,4]] |
Компактные гиперболические трехмерные решения
[ редактировать ]Решения с плотностью 1: ( Выпуклые однородные соты в гиперболическом пространстве ) ( Диаграмма Коксетера#Компакт (симплексные группы Ланнера) )
| Тип графика | Линейный | Трезубый | |||||
|---|---|---|---|---|---|---|---|
| Группа Коксетера Диаграмма Кокстера | [3,5,3] | [5,3,4] | [5,3,5] | [5,3 1,1 ]  | |||
| Вершинные фигуры из всеусеченных сот | |||||||
| Тетраэдр |  |  |  |  | |||
| Тетраэдр Симметрия | [2] + (заказ 2) | [ ] + (заказ 1) | [2] + (заказ 2) | [ ] (заказ 2) | |||
| Расширенная симметрия | [2 + [3,5,3]]  | [5,3,4] | [2 + [5,3,5]]  | [1[5,3 1,1 ]]  =[5,3,4] | |||
| Тип графика | Петля | ||||||
| Группа Коксетера Диаграмма Кокстера | [(4,3,3,3)] | [(4,3) 2 ] | [(5,3,3,3)] | [(5,3,4,3)] | [(5,3) 2 ] | ||
| Вершинные фигуры из всеусеченных сот | |||||||
| Тетраэдр |  |  |  |  |  | ||
| Тетраэдр Симметрия | [2] + (заказ 2) | [2,2] + (заказ 4)  | [2] + (заказ 2) | [2] + (заказ 2) | [2,2] + (заказ 4) | ||
| Расширенная симметрия | [2 + [(4,3,3,3)]] | [(2,2) + [(4,3) 2 ]] | [2 + [(5,3,3,3)]] | [2 + [(5,3,4,3)]] | [(2,2) + [(5,3) 2 ]] | ||
Паракомпактные гиперболические трехмерные решения
[ редактировать ]
Решения плотности 1: (См. диаграмму Коксетера # Паракомпакт (симплексные группы Кошуля) )
| Тип графика | Линейные графики | |||||||
|---|---|---|---|---|---|---|---|---|
| Группа Коксетера и диаграмма | [6,3,3] | [3,6,3] | [6,3,4] | [6,3,5] | [6,3,6] | [4,4,3] | [4,4,4] | |
| Тетраэдр симметрия | [ ] + (заказ 1) | [2] + (заказ 2) | [ ] + (заказ 1) | [ ] + (заказ 1) | [2] + (заказ 2) | [ ] + (заказ 1) | [2] + (заказ 2) | |
| Расширенная симметрия | [6,3,3] | [2 + [3,6,3]]  | [6,3,4] | [6,3,5] | [2 + [6,3,6]]  | [4,4,3] | [2 + [4,4,4]] | |
| Тип графика | Циклические графики | |||||||
| Группа Коксетера и диаграмма | [3 [ ]×[ ] ] | [(4,4,3,3)]  | [(4 3 ,3)] | [4 [4] ] | [(6,3 3 )] | [(6,3,4,3)] | [(6,3,5,3)] | [(6,3) [2] ] |
| Тетраэдр симметрия | [2] (заказ 4) | [ ] (заказ 2) | [2] + (заказ 2) | [2 + ,4] (заказ 8) | [2] + (заказ 2) | [2] + (заказ 2) | [2] + (заказ 2) | [2,2] + (заказ 4) |
| Расширенная симметрия | [2[3 [ ]×[ ] ]] =[6,3,4] | [1[(4,4,3,3)]] =[3,4 1,1 ]   | [2 + [(4 3 ,3)]] | [(2 + ,4)[4 [4] ]] =[2 + [4,4,4]] | [2 + [(6,3 3 )]] | [2 + [(6,3,4,3)]] | [2 + [(6,3,5,3)]] | [(2,2) + [(6,3) [2] ]] |
| Тип графика | Трезубый | Петля и хвост | Симплекс | |||||
| Группа Коксетера и диаграмма | [6,3 1,1 ] | [3,4 1,1 ] | [4 1,1,1 ] | [3,3 [3] ] | [4,3 [3] ] | [5,3 [3] ] | [6,3 [3] ] | [3 [3,3] ]  |
| Тетраэдр симметрия | [ ] (заказ 2) | [ ] (заказ 2) | [3] (заказ 6) | [ ] (заказ 2) | [ ] (заказ 2) | [ ] (заказ 2) | [ ] (заказ 2) | [3,3] (заказ 24) |
| Расширенная симметрия | [1[6,3 1,1 ]] =[6,3,4] | [1[3,4 1,1 ]] =[3,4,4] | [3[4 1,1,1 ]] =[4,4,3] | [1[3,3 [3] ]]  =[3,3,6] | [1[4,3 [3] ]] =[4,3,6] | [1[5,3 [3] ]] =[5,3,6] | [1[6,3 [3] ]] =[6,3,6] | [(3,3)[3 [3,3] ]] =[6,3,3] |
Рациональные решения
[ редактировать ]Существуют сотни рациональных решений для 3-сферы , включая эти 6 линейных графов, порождающих полихору Шлефли-Гесса , и 11 нелинейных графов Коксетера:
Линейные графики
| Петлевые графики:
|
Всего существует 59 спорадических тетраэдров с рациональными углами и 2 бесконечных семейства. [1]
См. также
[ редактировать ]- Группа точек для n -симплексных решений на ( n -1)-сфере.
Ссылки
[ редактировать ]- ^ https://arxiv.org/abs/2011.14232 Пространственные векторы, образующие рациональные углы, Киран С. Кедлая, Александр Колпаков, Бьорн Пунен, Майкл Рубинштейн, 2020
- Правильные многогранники (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8 (стр. 280, тетраэдры Гурса) [1]
- Норман Джонсон. Теория однородных многогранников и сот , доктор философии. (1966) Он доказал, что перечисление тетраэдров Гурса Коксетером является полным.
- Гурса, Эдуард, Об ортогональных заменах и регулярном разделении пространства , Annales Scientifiques de l'École Normale Supérieure, Ser. 3, 6 (1889), (с. 9–102, стр. 80–81 тетраэдры)
- Клитцинг, Ричард. «Диаграммы Дынкина, тетраэдры Гурса» .
- Норман Джонсон , Геометрии и трансформации (2018), главы 11,12,13
- Н. В. Джонсон , Р. Келлерхалс , Дж. Г. Рэтклифф, С. Т. Чанц, Размер гиперболического симплекса Кокстера , Группы преобразований 1999, Том 4, Выпуск 4, стр. 329–353 [2]