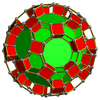
Шестиугольная призма

Однородная шестиугольная призма

Тип	Призматический однородный многогранник
Элементы	F = 8, E = 18, V = 12 (χ = 2)
Лица по сторонам	6{4}+2{6}
Символ Шлефли	t{2,6} или {6}×{}
Символ Витхоффа	2 6 \| 2 2 2 3 \|
Диаграммы Кокстера
Симметрия	D _6h , [6,2], (*622), порядок 24
Группа ротации	Д ₆ , [6,2] ⁺, (622), порядок 12
Ссылки	У _76(д)
Двойной	Шестиугольная дипирамида
Характеристики	выпуклый , зоноэдр
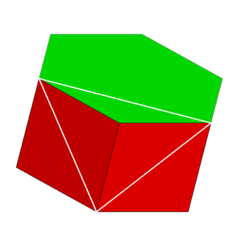Вершинная фигура 4.4.6

В геометрии шестиугольная призма — это призма с шестиугольным основанием. Призмы — это многогранники ; у этого многогранника 8 граней , 18 ребер и 12 вершин . ^[1]

Поскольку у него 8 граней, это октаэдр . Однако термин октаэдр в основном используется для обозначения правильного октаэдра , который имеет восемь треугольных граней. Из-за неоднозначности термина «октаэдр» и многогранности различных восьмигранных фигур этот термин редко используется без разъяснений.

перед заточкой Многие карандаши принимают форму длинной шестиугольной призмы. ^[2]

Как полуправильный (или однородный) многогранник

Если все грани правильные, шестиугольная призма представляет собой полуправильный многогранник , в более общем смысле, однородный многогранник и четвертую в бесконечном наборе призм, образованных квадратными сторонами и двумя правильными многоугольными вершинами. Его можно рассматривать как усеченный шестиугольный осоэдр , представленный символом Шлефли t{2,6}. Альтернативно его можно рассматривать как декартово произведение правильного шестиугольника и отрезка прямой и представить произведением {6}×{}. Двойственной шестиугольной призме является шестиугольная бипирамида .

Группа симметрии правой шестиугольной призмы — D _6h порядка 24. Группа вращения — D ₆ порядка 12.

Объем

Как и в большинстве призм, объем находится путем определения площади основания с длиной стороны $a$ и умножив его на высоту $h$ , давая формулу: ^[3]

$V={\frac {3{\sqrt {3}}}{2}}a^{2}\times h$ и площадь его поверхности может быть $S=3a({\sqrt {3}}a+2h)$ .

Симметрия

Топология однородной шестиугольной призмы может иметь геометрические варианты более низкой симметрии, в том числе:

Симметрия	Д _6h , [2,6], (*622)	С _6в , [6], (*66)	Д _3ч , [2,3], (*322)		Д _3д , [2 ⁺,6], (2*3)
Имя	Правильная шестиугольная призма	Шестиугольная деталь	Дитригональная призма	Триамбическая призма	Дитригональная трапезопризма
Строительство	{6}×{},		т{3}×{},		с2 _{ 2,6},
Изображение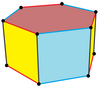
Искажение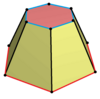

Как часть пространственной мозаики

Он существует в виде ячеек четырех призматических однородных выпуклых сот в трех измерениях:

Шестиугольные призматические соты ^[1]	Треугольно-шестиугольные призматические соты	Курносые треугольно-шестиугольные призматические соты	Ромботреугольно-шестиугольные призматические соты

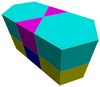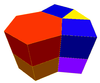Он также существует в виде ячеек ряда четырехмерных однородных 4-многогранников , в том числе:

Связанные многогранники и мозаики

Однородные шестиугольные двугранные сферические многогранники
Symmetry: [6,2], (*622)							[6,2]⁺, (622)	[6,2⁺], (2*3)


{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{6,2}	tr{6,2}	sr{6,2}	s{2,6}
Duals to uniforms

V6²	V12²	V6²	V4.4.6	V2⁶	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Этот многогранник можно считать членом последовательности однородных узоров с фигурой вершины (4.6.2p) и диаграммой Кокстера-Дынкина. . Для p < 6 членами последовательности являются всеусеченные многогранники ( зоноэдры ), показанные ниже в виде сферических мозаик. При p > 6 они представляют собой мозаику гиперболической плоскости, начиная с усеченной тригептагональной мозаики .

* n 32 мутация симметрии всеусеченных мозаик: 4.6.2n v т и
Sym. *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paraco.	Noncompact hyperbolic
Sym. *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Figures
Config.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duals
Config.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

См. также

Семейство однородных n -угольных призм v т и
Prism name	Digonal prism	(Trigonal) Triangular prism	(Tetragonal) Square prism	Pentagonal prism	Hexagonal prism	Heptagonal prism	Octagonal prism	Enneagonal prism	Decagonal prism	Hendecagonal prism	Dodecagonal prism	...	Apeirogonal prism
Polyhedron image												...
Spherical tiling image												Plane tiling image
Vertex config.	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	...	∞.4.4
Coxeter diagram												...

Ссылки

↑ Перейти обратно: Перейти обратно: ^а ^б Пью, Энтони (1976), Многогранники: визуальный подход , University of California Press, стр. 21, 27, 62, ISBN 9780520030565 .
^ Симпсон, Одри (2011), Основная математика для Кембриджа IGCSE , Cambridge University Press, стр. 266–267, ISBN 9780521727921 .
^ Уитер, Кэролайн К. (2007), Геометрия , Career Press, стр. 236–237, ISBN 9781564149367 .

Внешние ссылки

Однородные соты в трехмерных моделях VRML
Однородные многогранники
Многогранники виртуальной реальности Энциклопедия многогранников Призмы и антипризмы
Вайсштейн, Эрик В. «Шестиугольная призма» . Математический мир .
Интерактивная модель шестиугольной призмы — работает в вашем веб-браузере.

Эта многогранникам, статья, посвященная незавершена . Вы можете помочь Википедии, расширив ее .

[pugh-1] Перейти обратно: Перейти обратно: ^а ^б Пью, Энтони (1976), Многогранники: визуальный подход , University of California Press, стр. 21, 27, 62, ISBN 9780520030565 .

[2] Симпсон, Одри (2011), Основная математика для Кембриджа IGCSE , Cambridge University Press, стр. 266–267, ISBN 9780521727921 .

[3] Уитер, Кэролайн К. (2007), Геометрия , Career Press, стр. 236–237, ISBN 9781564149367 .

[1]

[2]

[3]

усеченная тетраэдрическая призма	усеченная октаэдрическая призма	Усеченная кубооктаэдрическая призма	Усеченная икосаэдрическая призма	Усеченная икосододекаэдральная призма

укороченный 5-клеточный	всеусеченный 5-клеточный	усеченный, 16-клеточный	всеусеченный тессеракт

усеченный, 24-клеточный	всеусеченный 24-клеточный	укороченный, 600 ячеек	всеусеченный, 120-ячеечный