Шестиугольный трапецоэдр
| Шестиугольный трапецоэдр | |
|---|---|
 | |
| Тип | трапецоэдр |
| Лица | 12 воздушных змеев |
| Края | 24 |
| Вершины | 14 |
| Конфигурация вершин | Версия 6.3.3.3 |
| Диаграмма Кокстера |      |
| Группа симметрии | Д 6д , [2 + ,12], (2*6), порядок 24 |
| Группа вращения | Д 6 , [2,6] + , (66), порядок 12 |
| Двойной многогранник | шестиугольная антипризма |
| Характеристики | выпуклый , гране-транзитивный |
В геометрии шестиугольный трапецоэдр или дельтоэдр является четвертым в бесконечной серии трапецоэдров, являются двойственными антипризмам которые многогранниками . У него двенадцать граней, которые представляют собой одинаковые воздушные змеи . Его можно описать обозначением Конвея dA6 .
Это изоэдральная (транзитивная по граням) фигура, то есть все ее грани одинаковы. Точнее, все грани не просто конгруэнтны, но и транзитивны , т.е. лежат на одной и той же орбите симметрии . Выпуклые равногранные многогранники — это формы, из которых можно составить игральные кости . [1]
Симметрия
[ редактировать ]Симметрия 6d шестиугольного трапецоэдра — D порядка 24. Группа вращения — D 6 порядка 12.
Вариации
[ редактировать ]Одна степень свободы в пределах симметрии D 6 превращает воздушные змеи в конгруэнтные четырехугольники с тремя длинами ребер. В пределе одно ребро каждого четырехугольника достигает нулевой длины, и они становятся бипирамидами .
Кристаллические расположения атомов могут повторяться в пространстве с гексагональной трапецоэдрической конфигурацией вокруг одного атома, которая всегда энантиоморфна . [2] и включает пространственные группы 177–182. [3] Бета-кварц — единственный распространенный минерал этой кристаллической системы. [4]
Если воздушные змеи, окружающие две вершины, имеют разную форму, они могут иметь только симметрию C 6v , порядка 12. Их можно назвать неравными трапецоэдрами . Дуал — это неравная антипризма с верхним и нижним многоугольниками разных радиусов. Если он искривлен и неравномерен, его симметрия снижается до циклической симметрии, . симметрии С6, порядка 6
| Тип | Скрученные трапецииэдры ( изоэдральные ) | Неравные трапецииэдры | Неравный и искривленный | |
|---|---|---|---|---|
| Симметрия | Д 6 , (662), [6,2] + , заказать 12 | С 6в , (*66), [6], порядок 12 | С 6 , (66), [6] + , заказ 6 | |
| Изображение ( п =6) |  |  |  |  |
| Сеть |  |  |  |  |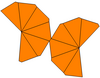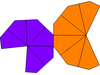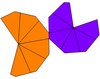
Сферическая черепица
[ редактировать ]Шестиугольный трапецоэдр также существует в виде сферической мозаики с двумя вершинами на полюсах и чередующимися вершинами, расположенными на равном расстоянии друг от друга над и под экватором.
Связанные многогранники
[ редактировать ]| Однородные шестиугольные двугранные сферические многогранники |
|---|
| трапецоэдра Название | Диагональный трапецоэдр ( Тетраэдр ) | Трехугольный трапецоэдр | Тетрагональный трапецоэдр | Пятиугольный трапецоэдр | Шестиугольный трапецоэдр | ... | Апейрогональный трапецоэдр |
|---|---|---|---|---|---|---|---|
| многогранника Изображение |  |  |  |  |  | ... | |
| Сферическое мозаичное изображение |  |  |  |  |  | Плоское мозаичное изображение |  |
| Конфигурация лица | В2.3.3.3 | В3.3.3.3 | Версия 4.3.3.3 | Версия 5.3.3.3 | Версия 6.3.3.3 | ... | V∞.3.3.3 |
Ссылки
[ редактировать ]- ^ Маклин, К. Робин (1990), «Подземелья, драконы и кости», The Mathematical Gazette , 74 (469): 243–256, doi : 10.2307/3619822 , JSTOR 3619822 .
- ^ 3 2 и Шестиугольно-трапецоэдрический класс, 6 2 2
- ^ Хан, Тео, изд. (2005). Международные таблицы для кристаллографии (5-е изд.). Дордрехт, Нидерланды: Опубликовано Springer для Международного союза кристаллографии. ISBN 978-0-7923-6590-7 .
- ^ «Кристаллография: гексагональная система» . www.mindat.org . Проверено 6 января 2023 г.
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. «Трапецоэдр» . Математический мир .
- Многогранники виртуальной реальности Энциклопедия многогранников
 | Эта многогранникам, статья, посвященная незавершена . Вы можете помочь Википедии, расширив ее . |