Трапецоэдр
| Набор двойственно-однородных n -угольных трапеций | |
|---|---|
 Пример: двойственно-однородный пятиугольный трапецоэдр ( n = 5 ). | |
| Тип | двойственно- однородный в смысле двойственно- полуправильный многогранник |
| Лица | 2 n одинаковых воздушных змеев |
| Края | 4 n |
| Вершины | 2н 2 + |
| Конфигурация вершин | В3.3.3. н |
| Символ Шлефли | { } ⨁ { п } [1] |
| Обозначение Конвея | дА н |
| Диаграмма Кокстера | |
| Группа симметрии | Д н д , [2 + ,2 n ], (2* n ), порядка 4 n |
| Группа ротации | Д н , [2, н ] + , (22 n ), порядок 2 n |
| Двойной многогранник | (выпуклая) равномерная n -угольная антипризма |
| Характеристики | выпуклые , грани-транзитивные , правильные вершины [2] |
В геометрии это n -угольный трапецоэдр , n -трапецоэдр , n -антидипирамида , n -антибипирамида или n -дельтоэдр. [3] , [4] — многогранник антипризмы n -угольной . двойственный граней 2 n -трапецоэдра n ; конгруэнтны порядке и расположены симметрично в шахматном их называют скрученными воздушными змеями . При более высокой симметрии его 2 n граней представляют собой воздушные змеи (иногда называемые также трапециями или дельтоидами ). [5]
« n -угольная » часть имени здесь относится не к граням, а к двум расположениям каждых n вершин вокруг оси n -кратной симметрии. Двойная n -угольная антипризма имеет две действительные n- угольные грани.
n - угольный трапецоэдр можно разрезать на две равные n -угольные пирамиды и n -угольную антипризму .
Терминология
[ редактировать ]Эти фигуры, иногда называемые дельто - эдрами, [3] не следует путать дельтой хедрой с , [4] грани которых представляют собой равносторонние треугольники.
Скрученные тригональные , тетрагональные и шестиугольные трапецоэдры (с шестью, восемью и двенадцатью скрученными конгруэнтными гранями) существуют в виде кристаллов; в кристаллографии (описывающей кристаллические особенности минералов трапецоэдрами ) их называют просто тригональными , тетрагональными и шестиугольными . У них нет ни плоскости симметрии, ни центра инверсионной симметрии; [6] , [7] но у них есть центр симметрии : точка пересечения их осей симметрии. Тригональный трапецоэдр имеет одну ось симметрии 3-го порядка, перпендикулярную трем осям симметрии 2-го порядка. [6] Тетрагональный трапецоэдр имеет одну ось симметрии 4-го порядка, перпендикулярную четырем осям симметрии 2-го порядка двух видов. Шестиугольный трапецоэдр имеет одну ось симметрии 6-го порядка, перпендикулярную шести осям симметрии 2-го порядка двух видов. [8]
Кристаллические расположения атомов могут повторяться в пространстве с ячейками тригональной и шестиугольной трапеции. [9]
Также в кристаллографии слово «трапецоэдр» часто используется для обозначения многогранника с 24 конгруэнтными нескрученными гранями, известного как дельтовидный икоситетраэдр . [10] который имеет восемнадцать вершин четвертого порядка и восемь вершин третьего порядка. Его не следует путать с додекагональным трапецоэдром , который также имеет 24 конгруэнтных грани, но две вершины порядка 12 (то есть полюса) и два кольца по двенадцать вершин порядка 3 каждое.
До сих пор в кристаллографии дельтоидный додекаэдр [11] имеет 12 конгруэнтных нескрученных граней, шесть вершин четвертого порядка и восемь вершин третьего порядка (ромбдодекаэдр является частным случаем). Его не следует путать с шестиугольным трапецоэдром , у которого также есть 12 конгруэнтных граней. [8] но две вершины порядка 6 (т.е. полюса) и два кольца по шесть вершин порядка 3 каждое.
Формы
[ редактировать ]n гранями , -трапецоэдр определяется правильным зигзагообразным косым 2 n -угольным основанием, двумя симметричными вершинами без степени свободы прямо над и прямо под основанием, а также четырехугольными соединяющими каждую пару соседних базальных ребер с одной вершиной.
n n -трапецоэдр имеет две вершины на полярной оси и 2 n базальных вершин в двух правильных -угольных кольцах. Он имеет 2 n конгруэнтных граней змея и является изоэдральным .
| трапецоэдра Название | Диагональный трапецоэдр ( Тетраэдр ) | Трехугольный трапецоэдр | Тетрагональный трапецоэдр | Пятиугольный трапецоэдр | Шестиугольный трапецоэдр | ... | Апейрогональный трапецоэдр |
|---|---|---|---|---|---|---|---|
| многогранника Изображение |  |  |  |  | ... | ||
| Сферическое мозаичное изображение |  |  |  |  |  | Плоское мозаичное изображение | |
| Конфигурация лица | В2.3.3.3 | В3.3.3.3 | Версия 4.3.3.3 | Версия 5.3.3.3 | Версия 6.3.3.3 | ... | V∞.3.3.3 |
Особые случаи:
- п = 2 . Вырожденная форма трапецоэдра: геометрический тетраэдр с 6 вершинами, 8 ребрами и 4 вырожденными гранями воздушного змея , которые вырождаются в треугольники. Его двойник — вырожденная форма антипризмы : тоже тетраэдр.
- п = 3 . Двойник треугольной антипризмы : коршуны ромбы (или квадраты); следовательно, эти трапецоэдры также являются зоноэдрами . Их называют ромбоэдрами . Это кубы , масштабированные по диагонали тела. Это также параллелепипеды с равными ромбическими гранями.

Ромбоэдр 60° , расчлененный на центральный правильный октаэдр и два правильных тетраэдра. - Особым случаем ромбоэдра является тот, в котором ромбы, образующие грани, имеют углы 60° и 120° . Его можно разложить на два равных правильных тетраэдра и правильный октаэдр . Поскольку параллелепипеды могут заполнять пространство , то же самое может сделать и комбинация правильных тетраэдров и правильных октаэдров .
- п = 5 . Пятиугольный трапецоэдр — единственный многогранник, кроме платоновых тел, обычно используемый в качестве кубика в ролевых играх, таких как Dungeons & Dragons . Будучи выпуклым и транзитивным по граням , он делает хорошие игральные кости . Имея 10 сторон, его можно использовать при повторении для генерации любой требуемой равномерной вероятности в десятичном формате . используются два кубика разного цвета, Обычно для двух цифр обозначающие числа от 00 до 99 .
Симметрия
[ редактировать ]Группа симметрии n : -угольного трапецоэдра равна D n d = D n v порядка 4 n , за исключением случая n = 3 куб имеет большую группу симметрии O d порядка 48 = 4×(4× 3) , который имеет четыре версии D 3d в качестве подгрупп.
Группа вращения n O -трапецоэдра равна D n порядка 2 n , за исключением случая n = 3 : куб имеет большую группу вращения порядка 24 = 4×(2×3) , которая имеет четыре версии. группы D3 . как подгруппы
Примечание. Каждый n -трапецоэдр с правильным зигзагообразным скошенным основанием из 2 n -угольников и 2 n конгруэнтными нескрученными гранями змея имеет ту же (диэдральную) группу симметрии, что и двойственно-однородный n -трапецоэдр, для n ≥ 4 .
Одна степень свободы в пределах симметрии от D n d (порядок 4 n ) до D n (порядок 2 n ) превращает конгруэнтные змеи в конгруэнтные четырехугольники с тремя длинами ребер, называемые скрученными кайтами , а n -трапецоэдр называется скрученным трапецоэдром . (В пределе одно ребро каждого четырёхугольника достигает нулевой длины, и n -трапецоэдр становится n - бипирамидой .)
Если змеи, окружающие две вершины, не скручены, а имеют две разные формы, n -трапецоэдр может иметь только симметрию C n v (циклическая с вертикальными зеркалами), порядка 2 n , и называется неравным или асимметричным трапецоэдром . Ее двойник представляет собой неравную n - антипризму , у которой верхний и нижний n -угольники разных радиусов.
Если змеи скручены и имеют две разные формы, n -трапецоэдр может иметь только C n (циклическую) симметрию, порядок n , и называется неравным скрученным трапецоэдром .
| Тип трапецоэдра | Витой трапецоэдр | Неравный трапецоэдр | Неравный скрученный трапецоэдр | |
|---|---|---|---|---|
| Группа симметрии | Д 6 , (662), [6,2] + | С 6в , (*66), [6] | С 6 , (66), [6] + | |
| Изображение многогранника | 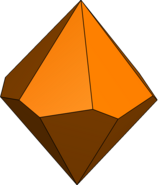 |  |  |  |
| Сеть |  | 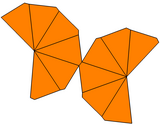 | 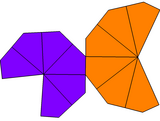 |  |
Звездчатый трапецоэдр
[ редактировать ]Звездчатый с p / q -трапецоэдр (где 2 ≤ q < 1 p ) определяется правильной зигзагообразной косой звездой 2 p / q -угольным основанием, двумя симметричными вершинами без степени свободы прямо над и прямо под основанием, и четырехсторонние грани, соединяющие каждую пару соседних базальных ребер с одной вершиной.
Звездчатый p / q -трапецоэдр имеет на своей полярной оси две вершинные вершины и 2 p- базальные вершины в двух правильных p -угольных кольцах. У него 2 p конгруэнтных граней змея , и он изоэдральный .
Такой звездчатый p / q -трапецоэдр представляет собой самопересекающуюся , скрещенную или невыпуклую форму. Он существует для любой правильной зигзагообразной косой звезды с основанием 2 p / q -угольника (где 2 ≤ q < 1 p ).
Но если п / q < 3 / 2 , тогда ( п - q ) 360° / п < q / 2 360° / p , поэтому двойная звездная антипризма (звездного трапецоэдра) не может быть однородной (т. е. не может иметь равные длины ребер); и если p / q = 3 / 2 , тогда ( п - q ) 360° / p = q / 2 360° / p , поэтому двойная звездная антипризма должна быть плоской, а значит, вырожденной, чтобы быть однородной.
Двойственно -однородный звездчатый p / q -трапецоэдр имеет диаграмму Кокстера-Дынкина. ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
| 5/2 | 5/3 | 7/2 | 7/3 | 7/4 | 8/3 | 8/5 | 9/2 | 9/4 | 9/5 |
|---|---|---|---|---|---|---|---|---|---|
 |  | ||||||||
| 10/3 | 11/2 | 11/3 | 11/4 | 11/5 | 11/6 | 11/7 | 12/5 | 12/7 |
|---|---|---|---|---|---|---|---|---|
См. также
[ редактировать ]- Уменьшенный трапецоэдр
- Ромбический додекаэдр
- Ромбический триаконтаэдр
- Бипирамида
- Усеченный трапецоэдр
- Обозначение многогранника Конвея
- «Призрак тьмы » — рассказ Лавкрафта , в котором решающую роль играет вымышленный древний артефакт, известный как «Сияющий трапецоэдр».
Ссылки
[ редактировать ]- ^ Н. В. Джонсон : Геометрии и трансформации , (2018) ISBN 978-1-107-10340-5 Глава 11: Конечные группы симметрии , 11.3 Пирамиды, призмы и антипризмы, рисунок 11.3c
- ^ «двойственность» . maths.ac-noumea.nc . Проверено 19 октября 2020 г.
- ^ Jump up to: Перейти обратно: а б Вайсштейн, Эрик В. «Трапецоэдр» . Математический мир . Проверено 24 апреля 2024 г. Примечания: грани дельтоэдра являются дельтовидами ; (не перекрученный) воздушный змей или дельтовидная мышца может быть разделена на два равнобедренных треугольника или «дельты» (Δ), от основания к основанию.
- ^ Jump up to: Перейти обратно: а б Вайсштейн, Эрик В. «Дельтаэдр» . Математический мир . Проверено 28 апреля 2024 г.
- ^ Спенсер 1911 , с. 575 или с. 597 в Wikisource, КРИСТАЛЛОГРАФИЯ, 1. КУБИЧЕСКАЯ СИСТЕМА, ТЕТРАЭДРИЧЕСКИЙ КЛАСС, сноска: «[Дельтоид]: от греческой буквы δ, Δ; вообще предмет треугольной формы; также альтернативное название трапеции». Примечание: скрученный воздушный змей может выглядеть как трапеция и даже быть ей.
- ^ Jump up to: Перейти обратно: а б Спенсер 1911 , с. 581 или с. 603 в Wikisource, КРИСТАЛЛОГРАФИЯ, 6. ГЕКСАГОНАЛЬНАЯ СИСТЕМА, Ромбоэдрическое деление , ТРАПЕЗОЭДРИЧЕСКИЙ КЛАСС, ФИГ. 74.
- ^ Спенсер 1911 , с. 577 или с. 599 в Wikisource, КРИСТАЛЛОГРАФИЯ, 2. ТЕТРАГОНАЛЬНАЯ СИСТЕМА, ТРАПЕЦОЭДРАЛЬНЫЙ КЛАСС.
- ^ Jump up to: Перейти обратно: а б Спенсер 1911 , с. 582 или с. 604 в Wikisource, КРИСТАЛЛОГРАФИЯ, 6. ГЕКСАГОНАЛЬНАЯ СИСТЕМА, Шестиугольное деление , ТРАПЕЦОЭДРАЛЬНЫЙ КЛАСС.
- ^ Класс тригонально-трапецоэдра, 3 2 и класс гексагонально-трапецоэдра, 6 2 2
- ^ Спенсер 1911 , с. 574 или с. 596 в Wikisource, КРИСТАЛЛОГРАФИЯ, 1. КУБИЧЕСКАЯ СИСТЕМА, ГОЛОСИММЕТРИЧЕСКИЙ КЛАСС, РИС. 17.
- ^ Спенсер 1911 , с. 575 или с. 597 в Wikisource, КРИСТАЛЛОГРАФИЯ, 1. КУБИЧЕСКАЯ СИСТЕМА, ТЕТРАЭДРИЧЕСКИЙ КЛАСС, РИС. 27.
- Энтони Пью (1976). Многогранники: визуальный подход . Калифорния: Издательство Калифорнийского университета в Беркли. ISBN 0-520-03056-7 . Глава 4: Двойники архимедовых многогранников, призмы и антипризмы
- Спенсер, Леонард Джеймс (1911). . В Чисхолме, Хью (ред.). Британская энциклопедия . Том. 07 (11-е изд.). Издательство Кембриджского университета. стр. 569–591.
