Наклон многоугольника

Красные края этого четырехугольного дисфеноида представляют собой правильный зигзагообразный скошенный четырехугольник.

В геометрии — перекошенный многоугольник это многоугольник , вершины которого не все лежат в одной плоскости . Косые многоугольники должны иметь не менее четырех вершин . поверхность Внутренняя (или площадь) такого многоугольника не определена однозначно.

Косые бесконечные многоугольники (апейрогоны) имеют вершины, которые не все коллинеарны.

Зигзагообразный косой многоугольник или антипризматический многоугольник. имеет вершины, которые чередуются в двух параллельных плоскостях и, следовательно, должны быть четными.

Правильные косые многоугольники в трех измерениях (и правильные косые апейрогоны в двух измерениях) всегда являются зигзагообразными.

Наклон многоугольников в трех измерениях

Однородная n -угольная антипризма имеет 2 n -сторонний правильный косой многоугольник, определенный вдоль ее боковых ребер.

Правильный косой многоугольник — это точная симметричная реализация многоугольника в размерности больше 2. В трехмерном правильном косом многоугольнике вершины чередуются между двумя параллельными плоскостями.

Правильный косой n -угольник может быть задан символом Шлефли { p }#{} как смесь правильного многоугольника p и ортогонального отрезка { }. Операция симметрии между последовательными вершинами — это скользящее отражение .

Примеры показаны на однородных квадратных и пятиугольных антипризмах. Звездчатые антипризмы также генерируют правильные косые многоугольники с разным порядком соединения верхних и нижних многоугольников. Закрашенные верхний и нижний многоугольники нарисованы для структурной ясности и не являются частью наклонных многоугольников.

Правильные зигзагообразные косые многоугольники

Косой квадрат	Косой шестиугольник	Косой восьмиугольник	Наклон десятиугольника			Наклон додекагона
{4}#{ }	{6}#{ }	{8}#{ }	{10}#{ }	{5}#{ }	{5/2}#{ }	{12}#{ }
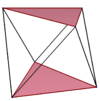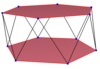с{2,4}	с{2,6}	с{2,8}	с{2,10}	ср{2,5/2}	с{2,10/3}	с{2,12}

Многоугольники Петри — это правильные косые многоугольники, определенные внутри правильных многогранников и многогранников. Например, пять Платоновых тел имеют 4-, 6- и 10-сторонние правильные косые многоугольники, как видно на этих ортогональных проекциях с красными краями вокруг соответствующих проективных оболочек . Тетраэдр и октаэдр включают в себя все вершины соответствующих зигзагообразных косых многоугольников и могут рассматриваться как двуугольная антипризма и треугольная антипризма соответственно.

Многоугольники Петри Платоновых тел

Правильный косой многоугольник как вершина правильного косого многогранника

Правильный косой многогранник имеет правильные грани многоугольника и фигуру вершины правильного косого многоугольника .

Три бесконечных правильных косых многогранника заполняют пространство в трехмерном пространстве; другие существуют в 4-мерном пространстве , некоторые — в однородных 4-многогранниках .

Косые вершинные фигуры трех бесконечных правильных косых многогранников

{4,6|4}	{6,4|4}	{6,6|3}
Правильный косой шестиугольник {3}#{ }	Обычный косой квадрат {2}#{ }	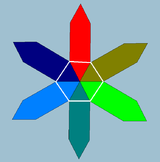Правильный косой шестиугольник {3}#{ }

Правильные косые многоугольники в четырех измерениях

В 4-х измерениях правильный косой многоугольник может иметь вершины на торе Клиффорда и быть связанным смещением Клиффорда . В отличие от зигзагообразных скошенных многоугольников, скошенные многоугольники при двойном вращении могут включать нечетное количество сторон.

Многоугольники Петри правильных 4-многогранников определяют правильные зигзагообразные косые многоугольники. Число Кокстера для каждой группы симметрии Кокстера показывает, сколько сторон имеет многоугольник Петри. Это 5 сторон для 5-ячеечного , 8 сторон для тессеракта и 16-ячеечного , 12 сторон для 24-ячеечного и 30 сторон для 120- и 600-ячеечного .

При ортогональном проецировании на плоскость Коксетера эти правильные косые многоугольники выглядят как оболочки правильных многоугольников на плоскости.

A 4 , [3,3,3]	Б 4 , [4,3,3]		Ф 4 , [3,4,3]	Ч 4 , [5,3,3]
Пентагон	Октагон		Додекагон	Триаконтагон
5-клеточный {3,3,3}	тессеракт {4,3,3}	16-ячеечный {3,3,4}	24-ячеечный {3,4,3}	120-ячеечный {5,3,3}	600-ячеечный {3,3,5}

дуопризмы n - n также и двойные дуопирамиды имеют 2 n -угольных многоугольника Петри. ( Тессеракт представляет собой дуопризму 4–4, а 16-клеточный — дуопирамиду 4–4.)

Шестиугольник		Декагон		Додекагон
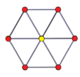3-3 дуопризма	3-3 дуопирамиды	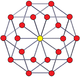5-5 дуопризма	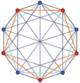5-5 дуопирамида	6-6 дуопризма	6-6 дуопирамиды

См. также

• Полигон Петри
• Четырехугольник § Перекос четырехугольников
• Правильный косой многогранник
• Косой апейроэдр (бесконечный косой многогранник)
• Наклонить линии

Ссылки

• МакМаллен, Питер ; Шульте, Эгон (декабрь 2002 г.), Абстрактные правильные многогранники (1-е изд.), Cambridge University Press , ISBN  0-521-81496-0 п. 25
• Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN  0-486-23729-Х . «Наклонные многоугольники (седловые многоугольники)» §2.2
• Коксетер, HSM (1973) [1948]. Правильные многогранники (3-е изд.). Нью-Йорк: Дувр.
• Коксетер , HSM; Правильные комплексные многогранники (1974). Глава 1. Правильные многоугольники , 1.5. Правильные многоугольники в n измерениях, 1.7. Зигзагообразные и антипризматические многоугольники , 1.8. Спиральные многоугольники . 4.3. Флаги и ортосхемы , 11.3. Полигоны Петри
• Коксетер , HSM « Полигоны Петри». Правильные многогранники , 3-е изд. Нью-Йорк: Дувр, 1973. (раздел 2.6 «Многоугольники Петри» , стр. 24–25, и глава 12, стр. 213–235, «Обобщенный многоугольник Петри» )
• Коксетер, HSM и Мозер, WOJ (1980). Генераторы и соотношения для дискретных групп . Нью-Йорк: Springer-Verlag. ISBN  0-387-09212-9 . (1-е изд., 1957 г.) 5.2 Многоугольник Петри {p,q}.
• Джон Милнор : О полной кривизне узлов , Энн. Математика. 52 (1950) 248–257.
• Дж. М. Салливан : Кривые конечной полной кривизны , ArXiv: math.0606007v2

Внешние ссылки

• Вайсштейн, Эрик В. «Наклонный многоугольник» . Математический мир .
• Вайсштейн, Эрик В. «Многоугольник Петри» . Математический мир .