Скольжение отражения


В геометрии скользящее отражение или трансфлексия — это геометрическое преобразование , состоящее из отражения через гиперплоскость и перемещения («скольжения») в направлении, параллельном этой гиперплоскости, объединенных в одно преобразование. Поскольку расстояния между точками не изменяются при скользящем отражении, это движение или изометрия . Когда контекстом является двумерная евклидова плоскость , гиперплоскость отражения представляет собой прямую линию, называемую линией скольжения или осью скольжения . Когда контекст представляет собой трехмерное пространство , гиперплоскость отражения представляет собой плоскость, называемую плоскостью скольжения . Вектор смещения трансляции называется вектором скольжения .
Когда какой-либо геометрический объект или конфигурация остаются неизмененными в результате преобразования, говорят, что он обладает симметрией , а преобразование называется операцией симметрии . Симметрия скольжения и отражения наблюдается в группах фризов (узоры, которые повторяются в одном измерении, часто используются в декоративных бордюрах), группах обоев (правильная мозаика плоскости) и пространственных группах (которые описывают, например, кристаллов симметрию ). Объекты с симметрией скольжения и отражения, как правило, не симметричны только при отражении , но два применения одного и того же отражения скольжения приводят к двойному перемещению, поэтому объекты с симметрией скольжения и отражения всегда также имеют простую трансляционную симметрию .
Когда отражение составлено с переносом в направлении, перпендикулярном гиперплоскости отражения, композиция двух преобразований представляет собой отражение в параллельной гиперплоскости. Однако, когда отражение состоит из перемещения в любом другом направлении, композиция двух преобразований представляет собой скользящее отражение, которое можно однозначно описать как отражение в параллельной гиперплоскости, составленное со сдвигом в направлении, параллельном гиперплоскости.
Одиночное скольжение представлено группой фризов p11g. Отражение скольжения можно рассматривать как предельное роторное отражение , при котором вращение становится поступательным. Ему также может быть присвоено обозначение Шенфлиса как S 2∞ , обозначение Кокстера как [∞ + ,2 + ] и обозначение орбифолда как ∞×.
Фризовые группы [ править ]
В евклидовой плоскости отражения и скользящие отражения — единственные два вида непрямых (изменяющих ориентацию) изометрий .
Например, существует изометрия, состоящая из отражения от оси x с последующим перемещением на одну единицу параллельно ей. В координатах это занимает
Эта изометрия отображает ось X сама на себя; любая другая линия, параллельная оси x , отражается от оси x , поэтому эта система параллельных линий остается инвариантной.
Группа изометрий, порожденная всего лишь скользящим отражением, представляет собой бесконечную циклическую группу . [1]
Объединение двух равных отражений скольжения дает чистый перевод с вектором перевода, который в два раза больше, чем у отражения скольжения, поэтому четные степени отражения скольжения образуют группу перевода.
В случае симметрии скользящего отражения группа симметрии объекта содержит скользящее отражение и, следовательно, группу, порожденную им. Если это все, что он содержит, то это группа фризов p11g.
Пример шаблона с этой группой симметрии: ![]()
Типичным примером отражения скольжения в повседневной жизни могут быть следы, оставленные на песке человеком, идущим по пляжу.
Группа фризов №. 6 (скользящие отражения, перемещения и вращения) генерируется скользящим отражением и вращением вокруг точки на линии отражения. Он изоморфен полупрямому произведению Z и C 2 .
Пример шаблона с этой группой симметрии: ![]()
Для любой группы симметрии, содержащей некоторую симметрию скользящего отражения, вектор трансляции любого скользящего отражения составляет половину элемента группы трансляции. Если вектор трансляции скользящего отражения сам по себе является элементом группы трансляции, то соответствующая симметрия скользящего отражения сводится к комбинации отражательной симметрии и трансляционной симметрии .
Группы обоев [ править ]
Симметрия скользящего отражения относительно двух параллельных линий с одинаковым сдвигом подразумевает, что существует также трансляционная симметрия в направлении, перпендикулярном этим линиям, с расстоянием перевода, которое в два раза превышает расстояние между линиями скользящего отражения. Это соответствует странице группы обоев ; при дополнительной симметрии он встречается также в pmg, pgg и p4g.
Если в том же направлении есть истинные линии отражения, то они равномерно расположены между линиями скользящего отражения. Линия скользящего отражения, параллельная линии истинного отражения, уже подразумевает такую ситуацию. Это соответствует группе обоев см. Трансляционная симметрия задается косыми векторами перемещения от одной точки на линии истинного отражения к двум точкам на следующей, поддерживая ромб с линией истинного отражения в качестве одной из диагоналей. При дополнительной симметрии он встречается также в cmm, p3m1, p31m, p4m и p6m.
В евклидовой плоскости 3 из 17 групп обоев требуют генераторов скользящего отражения. p2gg имеет ортогональные скользящие отражения и 2-кратное вращение. cm имеет параллельные зеркала и направляющие, а pg имеет параллельные направляющие. (Отражения скольжения показаны ниже пунктирными линиями)
| Кристаллографическое название | пгг | см | стр. |
|---|---|---|---|
| Имя Конвея | 22× | *× | ×× |
| Диаграмма |  |  | 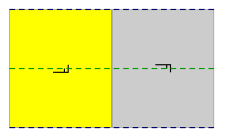 |
| Пример | 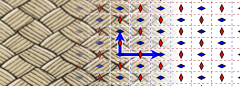 |  |  |
Пространственные группы [ править ]
Плоскости скольжения обозначаются в обозначениях Германа – Могена буквами a , b или c , в зависимости от того, по какой оси происходит скольжение. (Ориентация плоскости определяется положением символа в обозначении Германа – Могена.) Если ось не определена, то плоскость скольжения может быть обозначена буквой g . Когда плоскость скольжения параллельна экрану, эти плоскости могут быть обозначены изогнутой стрелкой, кончик которой указывает направление скольжения. Когда плоскость скольжения перпендикулярна экрану, эти плоскости могут быть представлены либо пунктирными линиями, когда скольжение параллельно плоскости экрана, либо пунктирными линиями, когда скольжение перпендикулярно плоскости экрана. Кроме того, центрированная решетка может привести к тому, что плоскость скольжения будет существовать в двух направлениях одновременно. Этот тип плоскости скольжения может обозначаться изогнутой стрелкой со стрелками с обеих сторон, когда плоскость скольжения параллельна плоскости экрана, или пунктирной двойной пунктирной линией, когда плоскость скольжения перпендикулярна плоскости экрана. . Существует также n -скольжение, которое представляет собой скольжение по половине диагонали грани, и d - скольжение, которое проходит по четвертой диагонали грани или пространства элементарной ячейки . Последнюю часто называют плоскостью скольжения алмаза, поскольку она является особенностью структуры алмаза. Плоскость скольжения n может быть обозначена диагональной стрелкой, если она параллельна плоскости экрана, или штрихпунктирной линией, если плоскость скольжения перпендикулярна плоскости экрана. Плоскость скольжения d может обозначаться диагональной полустрелкой, если плоскость скольжения параллельна плоскости экрана, или штрихпунктирной линией со стрелками, если плоскость скольжения перпендикулярна плоскости экрана. Если d , то этот кристалл должен иметь центрированную решетку. в кристаллической системе присутствует плоскость скольжения [2]
В сегодняшней версии обозначений Германа – Могена символ e используется в тех случаях, когда существует два возможных способа обозначения направления скольжения, поскольку оба верны. Например, если кристалл имеет решетку Браве с центром в основании и центром на грани C, то скольжение половины ячейки ячейки в направлении a дает тот же результат, что и скольжение половины ячейки ячейки в направлении b .
Группа изометрий, порожденная всего лишь скользящим отражением, представляет собой бесконечную циклическую группу . Объединение двух равных операций с плоскостью скольжения дает чистый сдвиг с вектором перемещения, который в два раза больше, чем у отражения скольжения, поэтому четные степени отражения скольжения образуют группу перемещения.
В случае симметрии скользящего отражения группа симметрии объекта содержит скользящее отражение и порожденную им группу. Для любой группы симметрии, содержащей отражение скольжения, вектор скольжения составляет половину элемента группы трансляции. Если вектор перемещения операции плоскости скольжения сам по себе является элементом группы перевода, то соответствующая симметрия плоскости скольжения сводится к комбинации симметрии отражения и симметрии поступательной .
Примеры и приложения [ править ]
Симметрию скольжения можно наблюдать в природе среди некоторых окаменелостей эдиакарской биоты ; махеридианцы ; и некоторые черви палеосколециды . [3] Его также можно увидеть во многих сохранившихся группах морских загонов . [4]
В «Игре жизни » Конвея часто встречающийся образец, называемый планёром, назван так потому, что он повторяет свою конфигурацию ячеек, сдвинутую отражением скольжения, после двух шагов автомата. После четырех шагов и двух скользящих отражений узор возвращается в исходную ориентацию, сдвинутую по диагонали на одну единицу. Продолжая таким образом, он перемещается по игровому массиву. [5]
См. также [ править ]
Примечания [ править ]
- ^ Мартин, Джордж Э. (1982). Геометрия преобразований: введение в симметрию . Тексты для бакалавриата по математике . Спрингер. п. 64. ИСБН 9780387906362 . .
- ^ «Скользящие самолеты» . Биркбек-колледж Лондонского университета . Архивировано из оригинала 21 июля 2019 года . Проверено 24 апреля 2019 г.
- ^ Ваггонер, Б.М. (1996). «Филогенетические гипотезы взаимоотношений членистоногих с проблемными ископаемыми таксонами докембрия и кембрия» . Систематическая биология . 45 (2): 190–222. дои : 10.2307/2413615 . JSTOR 2413615 .
- ^ Зуби, Тереза (2 января 2016 г.). «Октокораллы (столониферы, мягкие кораллы, морские веера, горгонарии, морские загоны) - Фотографии морских звезд - Восьмилучевые кораллы (трубчатые кораллы, мягкие кораллы, роговые кораллы, морские перья, веерные кораллы)» . starfish.ch . Архивировано из оригинала 11 августа 2022 г. Проверено 8 сентября 2016 г.
- ^ Уэйнрайт, Роберт Т. (1974). «Жизнь универсальна!». Материалы 7-й конференции по зимнему моделированию - WSC '74 . АКМ Пресс. дои : 10.1145/800290.811303 .
Ссылки [ править ]
- Уолтер Борхардт-Отт (1995). Кристаллография . Издательство Спрингер. ISBN 3-540-59478-7 .
Внешние ссылки [ править ]
- Glide Reflection. Архивировано 2006 г. в Wayback Machine. апреля 4