Параллельно (геометрия)

Эта статья о концепции геометрии. Чтобы узнать о других значениях, см. Параллельный (значения) .

Сюда перенаправляются «Параллельные линии» и «Параллельная линия». Чтобы узнать о других значениях, см. Параллельные линии (значения) .

Линейный рисунок параллельных линий и кривых.

В геометрии параллельные линии — это копланарные бесконечные прямые линии , не пересекающиеся ни в одной точке. Параллельные плоскости — это никогда не пересекающиеся плоскости в одном и том же трехмерном пространстве . Параллельные кривые — это кривые , которые не касаются друг друга, не пересекаются и сохраняют фиксированное минимальное расстояние. В трехмерном евклидовом пространстве линия и плоскость, не имеющие общей точки, также называются параллельными. Однако две некомпланарные линии называются косыми линиями . Отрезки прямых и евклидовы векторы параллельны, если они имеют одинаковое направление (не обязательно одинаковую длину).

Параллельные прямые являются предметом Евклида параллельности постулата . Параллелизм — это прежде всего свойство аффинной геометрии , а евклидова геометрия — частный случай этого типа геометрии. В некоторых других геометриях, таких как гиперболическая геометрия , линии могут иметь аналогичные свойства, которые называются параллельностью.

Символ

Параллельный символ $\parallel$. Например, $AB\parallel CD$ указывает, что линия AB параллельна линии CD .

В наборе символов Юникода знаки «параллельно» и «непараллельно» имеют кодовые точки U+2225 (∥) и U+2226 (∦) соответственно. Кроме того, U + 22D5 (⋕) представляет отношение «равно и параллельно».

Этот же символ используется для бинарной функции в электротехнике ( параллельный оператор ). Он отличается от скобок в виде двойной вертикальной линии U+2016 (‖), которые обозначают норму (например, $\|x\|$), а также из логического оператора или ( ||) на нескольких языках программирования.

Евклидов параллелизм

Две линии на плоскости

Условия параллелизма

Как показано делениями, прямые a и b параллельны. Это можно доказать, потому что трансверсаль t образует равные соответствующие углы. $\theta$, показанные здесь справа от поперечной линии: одна выше и рядом с линией a , а другая выше и рядом с линией b .

Учитывая параллельные прямые l и m в евклидовом пространстве , следующие свойства эквивалентны:

1. Каждая точка на линии m расположена на одинаковом (минимальном) расстоянии от линии l ( равноудаленные линии ).
2. Линия m лежит в той же плоскости, что и линия l, но не пересекает l (напомним, что линии простираются до бесконечности в любом направлении).
3. Когда линии m и l пересекаются третьей прямой линией ( трансверсалью ) в той же плоскости, соответствующие углы пересечения с трансверсалью равны .

Поскольку это эквивалентные свойства, любое из них можно принять за определение параллельных линий в евклидовом пространстве, но первое и третье свойства предполагают измерение и поэтому «более сложны», чем второе. Таким образом, второе свойство обычно выбирается в качестве определяющего свойства параллельных линий в евклидовой геометрии. Остальные свойства являются следствием постулата параллельности Евклида .

История

Определение параллельных линий как пары прямых линий на плоскости, которые не пересекаются, содержится в определении 23 в книге I « Начал» Евклида . Альтернативные определения обсуждались и другими греками, часто как часть попытки доказать постулат о параллельности . Прокл определение параллельных линий как равноудаленных линий приписывает Посидонию цитирует Близнеца и в том же духе . Симплиций также упоминает определение Посидония, а также его модификацию, предложенную философом Аганисом.

В конце девятнадцатого века в Англии «Начала» Евклида все еще оставались стандартным учебником в средних школах. Традиционное лечение геометрии было вынуждено измениться из-за новых разработок в проективной геометрии и неевклидовой геометрии , поэтому в это время было написано несколько новых учебников для преподавания геометрии. Основное различие между этими текстами реформ, как между ними, так и между ними и Евклидом, заключается в трактовке параллельных линий. Эти тексты реформ не остались без критиков, и один из них, Чарльз Доджсон (он же Льюис Кэрролл ), написал пьесу « Евклид и его современные соперники» , в которой эти тексты подвергаются критике.

Джеймса Мориса Уилсона Одним из первых учебников реформ была «Элементарная геометрия» 1868 года. Вильсон основал свое определение параллельных линий на понятии направления примитивном . По словам Вильгельма Киллинга эта идея может быть прослежена до Лейбница . Уилсон, не определяя направление, поскольку оно является примитивным, использует этот термин в других определениях, например в своем шестом определении: «Две прямые линии, которые встречаются друг с другом, имеют разные направления, и разница их направлений представляет собой угол между ними». Уилсон (1868 , стр. 2) В определении 15 он таким образом вводит параллельные прямые; «Прямые, имеющие одинаковое направление , но не являющиеся частями одной прямой, называются параллельными ». Уилсон (1868 , стр. 12) Огастес Де Морган рассмотрел этот текст и объявил его неудачным, прежде всего на основании этого определения и того, как Вильсон использовал его для доказательства вещей о параллельных прямых. Доджсон также посвящает большую часть своей пьесы (Акт II, сцена VI, § 1) осуждению подхода Уилсона к параллелям. Уилсон отредактировал эту концепцию из третьего и последующих изданий своего текста.

Другие свойства, предложенные другими реформаторами и использованные в качестве замены определения параллельных линий, оказались не намного лучше. Основная трудность, как указывал Доджсон, заключалась в том, что для их использования таким образом требовалось добавить в систему дополнительные аксиомы. Определение Посидония равноудаленной линии, изложенное Фрэнсисом Катбертсоном в его тексте 1874 года «Евклидова геометрия», страдает от проблемы, заключающейся в том, что точки, находящиеся на фиксированном заданном расстоянии на одной стороне прямой линии, должны быть показаны как образующие прямую линию. Это невозможно доказать и следует считать правдой. Соответствующие углы, образованные свойством трансверсальности, использованным У.Д. Кули в его тексте 1860 года « Элементы геометрии», упрощенные и объясненные, требуют доказательства того факта, что если одна трансверсаль встречается с парой прямых под конгруэнтными соответствующими углами, то все трансверсали должны соответствовать этому свойству. так. Опять же, необходима новая аксиома, чтобы обосновать это утверждение.

Строительство

Три вышеуказанных свойства приводят к трем различным методам построения. параллельных линий.

Задача: провести линию параллельную , l .

• 
  Свойство 1: Линия m везде имеет одинаковое расстояние до линии l .
• 
  Свойство 2. Проведите случайную прямую через a , которая пересекает l по x . Переместите точку x на бесконечность.
• 
  Свойство 3: И l , и m имеют общую поперечную линию, проходящую через a , которая пересекает их под углом 90 °.

Расстояние между двумя параллельными линиями

Основная статья: Расстояние между двумя линиями

Поскольку параллельные линии в евклидовой плоскости равноудалены, между двумя параллельными линиями существует уникальное расстояние. Учитывая уравнения двух невертикальных и негоризонтальных параллельных линий,

$y=mx+b_{1}\,$

$y=mx+b_{2}\,,$

расстояние между двумя линиями можно найти, найдя две точки (по одной на каждой линии), лежащие на общем перпендикуляре к параллельным линиям, и вычислив расстояние между ними. Поскольку линии имеют наклон m , общий перпендикуляр будет иметь наклон -1/ m , и мы можем взять линию с уравнением y = - x / m как общий перпендикуляр. Решите линейные системы

${\begin{cases}y=mx+b_{1}\\y=-x/m\end{cases}}$

и

${\begin{cases}y=mx+b_{2}\\y=-x/m\end{cases}}$

чтобы получить координаты точек. Решениями линейных систем являются точки

$\left(x_{1},y_{1}\right)\ =\left({\frac {-b_{1}m}{m^{2}+1}},{\frac {b_{1}}{m^{2}+1}}\right)\,$

и

$\left(x_{2},y_{2}\right)\ =\left({\frac {-b_{2}m}{m^{2}+1}},{\frac {b_{2}}{m^{2}+1}}\right).$

Эти формулы по-прежнему дают правильные координаты точки, даже если параллельные линии горизонтальны (т. е. m = 0). Расстояние между точками равно

$d={\sqrt {\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}}={\sqrt {\left({\frac {b_{1}m-b_{2}m}{m^{2}+1}}\right)^{2}+\left({\frac {b_{2}-b_{1}}{m^{2}+1}}\right)^{2}}}\,,$

что сводится к

$d={\frac {|b_{2}-b_{1}|}{\sqrt {m^{2}+1}}}\,.$

Когда линии заданы общим видом уравнения линии (включая горизонтальные и вертикальные линии):

$ax+by+c_{1}=0\,$

$ax+by+c_{2}=0,\,$

их расстояние можно выразить как

$d={\frac {|c_{2}-c_{1}|}{\sqrt {a^{2}+b^{2}}}}.$

Две линии в трёхмерном пространстве

Две линии в одном трехмерном пространстве , которые не пересекаются, не обязательно должны быть параллельными. Только если они находятся в общей плоскости, их называют параллельными; иначе их называют косыми линиями .

Две различные прямые l и m в трехмерном пространстве параллельны тогда и только тогда, когда расстояние от точки P на линии m до ближайшей точки на линии l не зависит от местоположения точки P на линии m . Это никогда не справедливо для перекошенных линий.

Линия и плоскость

Линия m и плоскость q в трехмерном пространстве, линия, не лежащая в этой плоскости, параллельны тогда и только тогда, когда они не пересекаются.

Эквивалентно, они параллельны тогда и только тогда, когда расстояние от точки P на линии m до ближайшей точки на плоскости q не зависит от местоположения точки P на линии m .

Два самолета

Подобно тому, как параллельные прямые должны располагаться в одной плоскости, параллельные плоскости должны располагаться в одном трёхмерном пространстве и не содержать общих точек.

Две различные плоскости q и r параллельны тогда и только тогда, когда расстояние от точки P в плоскости q до ближайшей точки в плоскости r не зависит от положения точки P в плоскости q . Этого никогда не будет, если две плоскости не находятся в одном и том же трехмерном пространстве.

В неевклидовой геометрии

В неевклидовой геометрии понятие прямой заменяется более общим понятием геодезической , кривой, которая является локально прямой относительно метрики (определения расстояния) на римановом многообразии , поверхности (или выше). многомерное пространство), которое само по себе может быть искривленным. В общей теории относительности частицы, не находящиеся под воздействием внешних сил, следуют геодезическим линиям в пространстве-времени , четырехмерном многообразии с тремя пространственными измерениями и одним временным измерением.

В неевклидовой геометрии ( эллиптическая или гиперболическая геометрия ) три упомянутых выше евклидовых свойства не эквивалентны, и только второе (линия m находится в той же плоскости, что и линия l, но не пересекает l) полезно в неевклидовой геометрии. поскольку оно не предполагает никаких измерений. В общей геометрии три вышеуказанных свойства дают три различных типа кривых: эквидистантные кривые , параллельные геодезические и геодезические, имеющие общий перпендикуляр соответственно.

Гиперболическая геометрия

Смотрите также: гиперболическая геометрия

Пересекающиеся , параллельные и ультрапараллельные прямые, проходящие через a относительно l в гиперболической плоскости. Кажется, что параллельные линии пересекаются недалеко от изображения. Это всего лишь артефакт визуализации. На реальной гиперболической плоскости линии сблизятся друг с другом и «встретятся» в бесконечности.

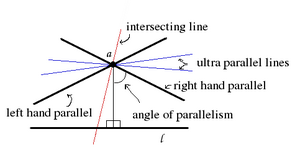
В то время как в евклидовой геометрии две геодезические могут либо пересекаться, либо быть параллельными, в гиперболической геометрии есть три возможности. Две геодезические, принадлежащие одной плоскости, могут быть:

1. пересекающиеся , если они пересекаются в одной точке плоскости,
2. параллельны , если они не пересекаются в плоскости, а сходятся к общей предельной точке на бесконечности ( идеальной точке ), или
3. ультрапараллельны , если они не имеют общей предельной точки на бесконечности.

В литературе ультрапараллельные геодезические часто называют непересекающимися . Геодезические, пересекающиеся на бесконечности, называются предельной параллелью .

Как и на рисунке, через точку a, не лежащую на прямой l, проходят две ограничивающие параллельные линии, по одной для каждого направления идеальной точки линии l. Они разделяют линии, пересекающие линию l, и те, которые ультрапараллельны линии l .

Ультрапараллельные прямые имеют один общий перпендикуляр ( теорема об ультрапараллели ) и расходятся по обе стороны от этого общего перпендикуляра.

Сферическая или эллиптическая геометрия

См. Также: Сферическая геометрия и Эллиптическая геометрия.

На сфере не существует параллельной линии. Линия a — это большой круг , эквивалент прямой линии в сферической геометрии. Линия c равноудалена от линии a , но не является большим кругом. Это параллель широты. Линия b — еще одна геодезическая, пересекающая а в двух противоположных точках. У них есть два общих перпендикуляра (один показан синим цветом).

В сферической геометрии все геодезические представляют собой большие круги . Большие круги делят сферу на два равных полушария , и все большие круги пересекаются друг с другом. Таким образом, не существует геодезических, параллельных данной геодезической, поскольку все геодезические пересекаются. Эквидистантные кривые на сфере называются параллелями широты, аналогично линиям широты на земном шаре. Параллели широты могут быть образованы пересечением сферы плоскостью, параллельной плоскости, проходящей через центр сферы.

Рефлексивный вариант

Если l, m, n — три различные прямые, то $l\parallel m\ \land \ m\parallel n\ \implies \ l\parallel n.$

В этом случае параллелизм является транзитивным отношением . Однако в случае l = n наложенные линии не считаются параллельными в евклидовой геометрии. Бинарное отношение между параллельными прямыми, очевидно, является симметричным отношением . Согласно принципам Евклида, параллелизм не является рефлексивным отношением и, следовательно, не может быть отношением эквивалентности . Тем не менее, в аффинной геометрии пучок . параллельных прямых рассматривается как класс эквивалентности в множестве прямых, где параллелизм является отношением эквивалентности

С этой целью Эмиль Артин (1957) принял определение параллельности, согласно которому две прямые параллельны, если у них есть все общие точки или ни одна из них. Тогда линия параллельна сама себе, так что рефлексивные и транзитивные свойства принадлежат этому типу параллелизма, создавая отношение эквивалентности на множестве прямых. При изучении геометрии инцидентности этот вариант параллелизма используется в аффинной плоскости .

См. также

• Клиффордская параллель
• Коллинеарность
• Параллельные линии
• Ограничивающая параллель
• Параллельная кривая
• Ультрапараллельная теорема

Ссылки

• Хит, Томас Л. (1956), Тринадцать книг элементов Евклида (2-е изд. [Факсимиле. Оригинальная публикация: Cambridge University Press, 1925] изд.), Нью-Йорк: Dover Publications

(3 тома): ISBN   0-486-60088-2 (т. 1), ISBN   0-486-60089-0 (т. 2), ISBN   0-486-60090-4 (т. 3). Авторитетный перевод Хита, а также обширные исторические исследования и подробные комментарии по всему тексту.

• Ричардс, Джоан Л. (1988), Математические видения: стремление к геометрии в викторианской Англии , Бостон: Academic Press, ISBN  0-12-587445-6
• Уилсон, Джеймс Морис (1868), Элементарная геометрия (1-е изд.), Лондон: Macmillan and Co.
• Уайли, Ч. Р. младший (1964), Основы геометрии , МакГроу – Хилл

Дальнейшее чтение

• Пападопулос, Афанасий; Тере, Гийом (2014), Теория параллелей Иоганна Генриха Ламберта: презентация, перевод и комментарии , Париж: Коллекция Sciences dans l'histoire, Librairie Albert Blanchard, ISBN  978-2-85367-266-5