Ограничивающая параллель

Две линии, проходящие через заданную точку P параллельны линии R. и ограничивающие ее ,

В нейтральной или абсолютной геометрии , а также в гиперболической геометрии может быть много линий, параллельных данной прямой. $l$ через точку $P$ не на линии $R$; однако в плоскости две параллели могут быть ближе к $l$ чем все остальные (по одному в каждом направлении $R$).

Таким образом, полезно дать новое определение параллелей в нейтральной геометрии. Если есть ближайшие параллели к данной линии, они известны как предельная параллель , асимптотическая параллель или хоропараллель (horo от греческого : ὅριον — граница).

Для лучей отношение предельной параллели является отношением эквивалентности , которое включает в себя отношение эквивалентности котерминальности.

Если в гиперболическом треугольнике пары сторон предельно параллельны, то треугольник является идеальным треугольником .

Определение

Луч Аа представляет собой предельную параллель Вb , записанную: $Aa|||Bb$

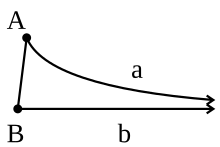
Луч ​ $Aa$ является предельной параллелью луча $Bb$ если они котерминальны или лежат на разных прямых, не равных прямой $AB$, они не встречаются, и каждый луч внутри угла $BAa$ встречает луч $Bb$.

Свойства

Четкие линии, несущие ограничивающие параллельные лучи, не пересекаются.

Доказательство

Предположим, что линии, несущие различные параллельные лучи, встретились. По определению они не могут встретиться на стороне $AB$ который либо $a$ включен. Тогда они должны встретиться на стороне $AB$ напротив $a$, позвоните в эту точку $C$. Таким образом $\angle CAB+\angle CBA<2{\text{ right angles}}\Rightarrow \angle aAB+\angle bBA>2{\text{ right angles}}$. Противоречие.

См. также

• horocycle , В гиперболической геометрии кривая , которой нормали являются предельными параллелями.
• угол параллельности