Большой круг

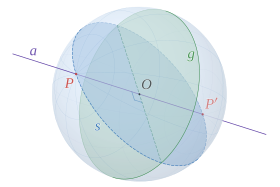
В математике большой круг или ортодром — это круговое пересечение сферы проходящей и плоскости, через сферы центр . ^[1]^[2]

Любая дуга большого круга является геодезической сферы, так что большие круги в сферической геометрии являются естественным аналогом прямых линий в евклидовом пространстве . Для любой пары различных неантиподальных точек на сфере существует единственный большой круг, проходящий через обе. (Каждый большой круг, проходящий через любую точку, также проходит через свою антиподальную точку, поэтому существует бесконечно много больших кругов, проходящих через две противоположные точки.) Более короткая из двух дуг большого круга между двумя различными точками на сфере называется малой дугой , и это кратчайший путь по поверхности между ними. его Длина дуги представляет собой по большому кругу расстояние между точками ( внутреннее расстояние на сфере) и пропорциональна мере центрального угла , образованного двумя точками и центром сферы.

Большой круг — это самый большой круг, который можно нарисовать на любой сфере. Любой диаметр любого большого круга совпадает с диаметром сферы, и, следовательно, каждый большой круг концентричен сфере и имеет тот же радиус . Любой другой круг сферы называется малым кругом и представляет собой пересечение сферы плоскостью, не проходящей через ее центр. Маленькие круги - это аналог кругов в евклидовом пространстве сферической геометрии.

Каждый круг в евклидовом трехмерном пространстве представляет собой большой круг, состоящий ровно из одной сферы.

Диск , ограниченный большим кругом, называется большим диском : это пересечение шара и плоскости, проходящей через его центр.В более высоких измерениях большие круги на n -сфере представляют собой пересечение n- сферы с двумя плоскостями, проходящими через начало координат в евклидовом пространстве $R. п + 1$ .

Вывод кратчайших путей [ править ]

Чтобы доказать, что малая дуга большого круга является кратчайшим путем, соединяющим две точки на поверхности сферы, можно применить вариационное исчисление к ней .

Рассмотрим класс всех правильных путей из точки $p$ в другую точку $q$ . Введем сферические координаты так, что $p$ совпадает с северным полюсом. Любая кривая на сфере, которая не пересекает ни один полюс, за исключением, возможно, конечных точек, может быть параметризована формулой

\theta =\theta (t),\quad \phi =\phi (t),\quad a\leq t\leq b

предоставил $\phi$ разрешено принимать произвольные действительные значения. Бесконечно малая длина дуги в этих координатах равна

ds=r{\sqrt {\theta '^{2}+\phi '^{2}\sin ^{2}\theta }}\,dt.

Итак, длина кривой $\gamma$ от $p$ к $q$ является функционалом кривой, заданной выражением

S[\gamma ]=r\int _{a}^{b}{\sqrt {\theta '^{2}+\phi '^{2}\sin ^{2}\theta }}\,dt.

Согласно уравнению Эйлера–Лагранжа , $S[\gamma ]$ минимизируется тогда и только тогда, когда

{\frac {\sin ^{2}\theta \phi '}{\sqrt {\theta '^{2}+\phi '^{2}\sin ^{2}\theta }}}=C

,

где $C$ это $t$ -независимая константа и

{\frac {\sin \theta \cos \theta \phi '^{2}}{\sqrt {\theta '^{2}+\phi '^{2}\sin ^{2}\theta }}}={\frac {d}{dt}}{\frac {\theta '}{\sqrt {\theta '^{2}+\phi '^{2}\sin ^{2}\theta }}}.

Из первого уравнения этих двух можно получить, что

\phi '={\frac {C\theta '}{\sin \theta {\sqrt {\sin ^{2}\theta -C^{2}}}}}

.

Интегрируя обе стороны и учитывая граничные условия, реальное решение $C$ равен нулю. Таким образом, $\phi '=0$ и $\theta$ может быть любым значением от 0 до $\theta _{0}$ , что указывает на то, что кривая должна лежать на меридиане сферы. В декартовой системе координат это

x\sin \phi _{0}-y\cos \phi _{0}=0

которая является плоскостью, проходящей через начало координат, т. е. центр сферы.

Приложения [ править ]

Некоторые примеры больших кругов на небесной сфере включают небесный горизонт , небесный экватор и эклиптику . Большие круги также используются как довольно точные приближения геодезических на поверхности Земли для воздушной или морской навигации (хотя она и не является идеальной сферой ), а также на сфероидальных небесных телах .

Экватор . идеализированной Земли представляет собой большой круг, а любой меридиан и противоположный ему меридиан образуют большой круг Еще один большой круг — тот, который разделяет сухопутное и водное полушария . Большой круг делит Землю на два полушария , и если большой круг проходит через какую-то точку, он должен пройти и через свою антиподную точку .

объединяет Преобразование Фанка функцию по всем большим кругам сферы.

См. также [ править ]

Ссылки [ править ]

^ В., Вайсштейн, Эрик. «Большой круг — из Wolfram MathWorld» . mathworld.wolfram.com . Проверено 30 сентября 2022 г. {{cite web}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Вайнрит, Адам; Копч, Петр (2014). Локсодромия (прямая линия), ортодромия (большой круг), большой эллипс и геодезическая линия (геодезическая) в навигации . США: CRC Press, Inc. ISBN. 978-1-138-00004-9 .

Внешние ссылки [ править ]

Большой круг - из описания, рисунков и уравнений MathWorld Great Circle. Mathworld, Wolfram Research, Inc., 1999 г.
«Большие круги на карте Меркатора» Джона Снайдера с дополнительным вкладом Джеффа Брайанта, Пратика Десаи и Карла Уолла, Демонстрационный проект Вольфрама .

[1] В., Вайсштейн, Эрик. «Большой круг — из Wolfram MathWorld» . mathworld.wolfram.com . Проверено 30 сентября 2022 г. {{cite web}}: CS1 maint: несколько имен: список авторов ( ссылка )

[2] Вайнрит, Адам; Копч, Петр (2014). Локсодромия (прямая линия), ортодромия (большой круг), большой эллипс и геодезическая линия (геодезическая) в навигации . США: CRC Press, Inc. ISBN. 978-1-138-00004-9 .

[1]

[2]