Эклиптика

Если смотреть с орбиты Земли , то кажется, что Солнце движется относительно неподвижных звезд , а эклиптика – это годовой путь, по которому Солнце следует на небесной сфере . Этот процесс повторяется в цикле продолжительностью чуть более 365 дней .

Эклиптика орбитальная или плоскость эклиптики — это плоскость Земли вокруг Солнца . С точки зрения наблюдателя на Земле движение Солнца по небесной сфере в течение года прослеживает путь по эклиптике на фоне звезд . Эклиптика является важной опорной плоскостью и основой эклиптической системы координат .

Видимое движение Солнца

Эклиптика – это видимый путь Солнца в течение года .

Поскольку Земле требуется один год, чтобы совершить оборот вокруг Солнца, кажущемуся положению Солнца требуется один год, чтобы совершить полный оборот вокруг эклиптики. Поскольку в году чуть больше 365 дней, Солнце перемещается чуть менее чем на 1° к востоку. каждый день. Эта небольшая разница в положении Солнца относительно звезд приводит к тому, что любая конкретная точка на поверхности Земли догоняет Солнце (и становится прямо к северу или югу от него) каждый день примерно на четыре минуты позже, чем это было бы, если бы Земля не вращалась по орбите; Таким образом, день на Земле длится 24 часа, а не звездные сутки продолжительностью примерно 23 часа 56 минут . Опять же, это упрощение, основанное на гипотетической Земле, которая вращается вокруг Солнца с одинаковой скоростью. Фактическая скорость, с которой Земля вращается вокруг Солнца, незначительно меняется в течение года, поэтому скорость, с которой Солнце движется по эклиптике, также меняется. Например, Солнце находится к северу от небесного экватора примерно 185 дней в году и к югу от него примерно 180 дней. Изменение орбитальной скорости является частью уравнения времени .

Из-за движения Земли вокруг центра масс Земля-Луна видимая траектория Солнца слегка колеблется с периодом около одного месяца . Из-за дальнейших возмущений со стороны других планет Солнечной системы Земли и Луны барицентр слегка колеблется вокруг среднего положения сложным образом.

небесным

Основная статья: Осевой наклон

Плоскость орбиты Земли , образует опорную плоскость , проецируемая во всех направлениях , известную как эклиптика. Здесь она показана проецированной наружу (серым цветом) на небесную сферу Земли вместе с экватором и полярной осью (зеленым цветом). Плоскость эклиптики пересекает небесную сферу по большому кругу (черному), тому же кругу, по которому, кажется, движется Солнце, когда Земля вращается вокруг него. Пересечения эклиптики и экватора на небесной сфере — это точки равноденствия (красные), где Солнце кажется пересекающим небесный экватор.

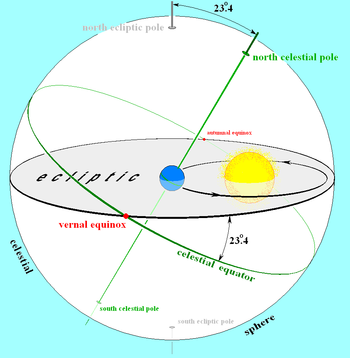
Поскольку ось вращения Земли не перпендикулярна плоскости ее орбиты Земли , экваториальная плоскость не копланарна плоскости эклиптики, а наклонена к ней на угол около 23,4°, который известен как наклон эклиптики . Если экватор проецируется наружу на небесную сферу , образуя небесный экватор , он пересекает эклиптику в двух точках, известных как точки равноденствия . Солнце в своем видимом движении по эклиптике пересекает небесный экватор в этих точках, одну с юга на север, другую с севера на юг. Пересечение с юга на север известно как мартовское равноденствие , также известное как первая точка Овна и восходящий узел эклиптики на небесном экваторе. Пересечение с севера на юг — это точка сентябрьского равноденствия или нисходящий узел .

Основная статья: Осевая прецессия

Ориентация оси Земли и экватора не фиксирована в пространстве, а вращается вокруг полюсов эклиптики с периодом около 26 000 лет, процесс, известный как лунно-солнечная прецессия , поскольку он обусловлен главным образом гравитационным воздействием Луны и Солнца . на экваториальной выпуклости Земли . Аналогично, сама эклиптика не является фиксированной. Гравитационные возмущения других тел Солнечной системы вызывают гораздо меньшее движение плоскости земной орбиты и, следовательно, эклиптики, известное как планетарная прецессия . Совместное действие этих двух движений называется общей прецессией и меняет положение точек равноденствия примерно на 50 угловых секунд (около 0,014°) в год.

Основная статья: Астрономическая нутация

Еще раз, это упрощение. Периодические движения Луны и кажущиеся периодические движения Солнца ( собственно Земли на ее орбите) вызывают кратковременные малоамплитудные периодические колебания земной оси и, следовательно, небесного экватора, известные как нутация . Это добавляет периодический компонент к положению равноденствий; положения небесного экватора и (мартового) равноденствия с полностью обновленными прецессией и нутацией называются истинным экватором и равноденствием ; положения без нутации — это средний экватор и равноденствие .

Наклон эклиптики

Основная статья: Наклон эклиптики

Наклон эклиптики — это термин, используемый астрономами для обозначения наклона экватора Земли по отношению к эклиптике или оси вращения Земли к перпендикуляру к эклиптике. Он составляет около 23,4° и в настоящее время уменьшается на 0,013 градуса (47 угловых секунд) за сто лет из-за планетарных возмущений.

Угловое значение наклона определяется путем наблюдения за движением Земли и других планет на протяжении многих лет. Астрономы создают новые фундаментальные эфемериды по мере повышения точности наблюдений и улучшения понимания динамики , и на основе этих эфемерид получают различные астрономические значения, включая наклон.

Наклон эклиптики за 20 000 лет по данным Ласкара (1986). Обратите внимание, что наклон за это время меняется всего от 24,2° до 22,5°. Красная точка представляет 2000 год.

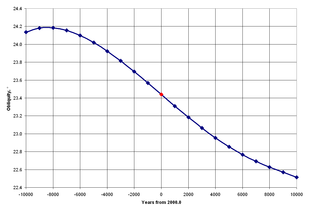
До 1983 года наклон для любой даты рассчитывался на основе работы Ньюкомба , который анализировал положения планет примерно до 1895 года:

ε = 23°27′08,26″ – 46,845″ Т – 0,0059″ Т. ² + 0,00181″ Т ³

где ε — наклон, а T — тропические столетия от B1900.0 до рассматриваемой даты.

С 1984 года DE Лаборатории реактивного движения серия компьютерных эфемерид стала фундаментальной эфемеридой Астрономического альманаха . Наклон на основе DE200, который анализировал наблюдения с 1911 по 1979 год, был рассчитан:

ε = 23°26′21,45″ – 46,815″ Т – 0,0006″ Т ² + 0,00181″ Т ³

где далее T — юлианские столетия от J2000.0 .

Фундаментальные эфемериды JPL постоянно обновляются. В Астрономическом альманахе за 2010 год указано:

ε = 23°26′21,406″ - 46,836769″ Т - 0,0001831″ Т ² + 0,00200340″ Т ³ − 0.576×10 ⁻⁶ ″ Т ⁴ − 4.34×10 ⁻⁸ ″ Т ⁵

Эти выражения для наклона предназначены для высокой точности в течение относительно короткого периода времени, возможно, нескольких столетий. Дж. Ласкар вычислил выражение порядка T ¹⁰ хорошо до 0,04 дюйма /1000 лет в течение 10 000 лет.

Все эти выражения относятся к среднему наклону, то есть без учета нутации экватора. Истинное или мгновенное отклонение включает нутацию.

Плоскость Солнечной системы

Основная статья: Солнечная система

Виды сверху и сбоку плоскости эклиптики, показывающие планеты Меркурий , Венеру , Землю и Марс . Большинство планет вращаются вокруг Солнца почти в той же плоскости, в которой вращается Земля, — эклиптике.		Пять планет (включая Землю) выстроились вдоль эклиптики в июле 2010 года, иллюстрируя, как планеты вращаются вокруг Солнца почти в одной плоскости. Фотография сделана на закате, вид на запад над Суракартой, Ява, Индонезия.

Большинство крупных тел Солнечной системы вращаются вокруг Солнца почти в одной плоскости. Вероятно, это связано с тем, как Солнечная система сформировалась из протопланетного диска . Вероятно, самое близкое современное представление диска известно как неизменная плоскость Солнечной системы . Орбита Земли, а следовательно, и эклиптика, наклонена к неизменной плоскости чуть более чем на 1°, орбита Юпитера находится в пределах чуть более ½° от нее, а все остальные большие планеты — в пределах примерно 6°. Из-за этого большинство тел Солнечной системы кажутся на небе очень близко к эклиптике.

Неизменная плоскость определяется угловым моментом всей Солнечной системы, по сути, векторной суммой всех орбитальных и вращательных угловых моментов всех тел системы; более 60% от общего количества приходится на орбиту Юпитера. Эта сумма требует точного знания каждого объекта в системе, что делает ее несколько неопределенной величиной. Из-за неопределенности относительно точного местоположения неизменной плоскости и поскольку эклиптика хорошо определяется видимым движением Солнца, эклиптика используется в качестве базовой плоскости Солнечной системы как для точности, так и для удобства. Единственный недостаток использования эклиптики вместо неизменной плоскости заключается в том, что в геологических масштабах времени она будет двигаться относительно фиксированных опорных точек на отдаленном фоне неба.

Небесная опорная плоскость

Основные статьи: Небесный экватор и эклиптическая система координат.

Видимое движение Солнца по эклиптике (красный цвет), как видно на внутренней стороне небесной сферы . Координаты эклиптики выделены (красным). Небесный экватор (синий) и экваториальные координаты (синий), наклоненные к эклиптике, кажутся колеблющимися по мере продвижения Солнца.

Эклиптика образует одну из двух основных плоскостей, используемых в качестве ориентира для определения положения на небесной сфере, другая — небесный экватор . Перпендикулярно эклиптике расположены полюса эклиптики , причем северный полюс эклиптики является полюсом к северу от экватора. Из двух фундаментальных плоскостей эклиптика ближе к неподвижной на фоне звезд, ее движение из-за планетарной прецессии составляет примерно 1/100 движения небесного экватора.

Сферические координаты , известные как эклиптическая долгота и широта или небесная долгота и широта, используются для указания положения тел на небесной сфере относительно эклиптики. Долгота измеряется положительно в восточном направлении. От 0° до 360° вдоль эклиптики от мартовского равноденствия, в том же направлении, в котором движется Солнце. Широта измеряется перпендикулярно эклиптике до +90 ° к северу или -90 ° к югу от полюсов эклиптики, причем сама эклиптика имеет широту 0 °. Для полного сферического положения также необходим параметр расстояния. Для разных объектов используются разные единицы расстояния. В пределах Солнечной системы используются астрономические единицы , а для объектов вблизи Земли — радиусы Земли или километры . соответствующая правосторонняя прямоугольная система координат Иногда также используется ; ось x направлена ​​к мартовскому равноденствию, ось y на 90° к востоку, а ось z к северному полюсу эклиптики; астрономическая единица – это единица измерения. Символы эклиптических координат несколько стандартизированы; см. таблицу.

Краткое описание обозначений эклиптических координат

	сферический			Прямоугольный
	Долгота	Широта	Расстояние
Геоцентрический	л	б	Д
гелиоцентрический	л	б	р	х , у , я

Координаты эклиптики удобны для указания положения объектов Солнечной системы, поскольку орбиты большинства планет имеют небольшой наклон к эклиптике и поэтому всегда кажутся относительно близкими к ней на небе. Поскольку орбита Земли и, следовательно, эклиптика движется очень мало, она является относительно фиксированной точкой отсчета по отношению к звездам.

Наклон эклиптики за 200 000 лет из Дзиобека (1892 г.). Это наклон к эклиптике 101 800 г. н. э. Заметим, что эклиптика за это время поворачивается всего лишь примерно на 7°, тогда как небесный экватор совершает несколько полных оборотов вокруг эклиптики. Эклиптика является относительно стабильной точкой отсчета по сравнению с небесным экватором.

Из-за прецессионного движения точки равноденствия эклиптические координаты объектов на небесной сфере непрерывно изменяются. Указание положения в эклиптических координатах требует указания конкретного равноденствия, то есть равноденствия определенной даты, известной как эпоха ; координаты относятся к направлению равноденствия в эту дату. Например, Астрономический альманах. перечисляет гелиоцентрическое положение Марса в 0 часов земного времени , 4 января 2010 года, как: долгота 118 ° 09′15,8 дюйма, широта + 1 ° 43′16,7 дюйма, истинное гелиоцентрическое расстояние 1,6302454 а.е., среднее равноденствие и эклиптика даты. Здесь указано среднее равноденствие 4 января 2010 г. в 0h TT, как указано выше , без добавления нутации.

Затмения

Основная статья: Затмение

Поскольку Земля вращается вокруг Солнца, приблизительная осевая параллельность плоскости орбиты Луны ( наклоненной на пять градусов к эклиптике) приводит к вращению лунных узлов относительно Земли. Это приводит к сезону затмений примерно каждые шесть месяцев, при котором солнечное затмение может произойти в фазу новолуния , а лунное затмение может произойти в фазу полнолуния .

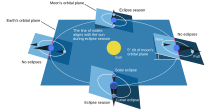
Поскольку орбита Луны наклонена к эклиптике лишь примерно на 5,145°, а Солнце всегда находится очень близко к эклиптике, затмения всегда происходят на ней или рядом с ней. Из-за наклона орбиты Луны затмения происходят не при каждом соединении и противостоянии Солнца и Луны, а только тогда, когда Луна находится рядом с восходящим или нисходящим узлом и одновременно находится в соединении ( новом ) или противостоянии ( полный ). Эклиптика названа так потому, что древние заметили, что затмения происходят только тогда, когда ее пересекает Луна.

Равноденствия и солнцестояния

Положения равноденствий и солнцестояний

	эклиптика	экваториальный
	долгота	прямое восхождение
мартовское равноденствие	0°	0ч
Июньское солнцестояние	90°	6 часов
Сентябрьское равноденствие	180°	12 часов
декабрьское солнцестояние	270°	18 часов

Основная статья: Равноденствие (небесные координаты)

Точные моменты равноденствий и солнцестояний — это времена, когда видимая эклиптическая долгота (включая эффекты аберрации и нутации ) Солнца составляет 0 °, 90 °, 180 ° и 270 °. Из-за возмущений орбиты Земли и аномалий календаря даты их не фиксированы.

В созвездиях

Равноугольный график склонения и прямого восхождения современных созвездий с пунктирной линией, обозначающей эклиптику. Созвездия имеют цветовую маркировку в зависимости от семейства и года основания.

В настоящее время эклиптика проходит через следующие созвездия :

• Рыбы
• Овен
• Телец
• Близнецы
• Рак
• Лео
• Дева
• Весы
• Скорпиус
• Змееносец
• Стрелец
• Козерог
• Водолей

Созвездия Кита и Ориона не находятся на эклиптике, но находятся достаточно близко, чтобы в них изредка могли появляться Луна и планеты.

Астрология

Основная статья: Астрология

Эклиптика образует центр зодиака , небесный пояс шириной около 20° по широте, через который всегда движутся Солнце, Луна и планеты. Традиционно этот регион делится на 12 знаков по 30° долготы, каждый из которых приблизительно соответствует движению Солнца за один месяц. В древние времена знаки соответствовали примерно 12 созвездиям, расположенным по обе стороны эклиптики. Эти знаки иногда до сих пор используются в современной терминологии. « Первая точка Овна » была названа, когда Солнце в день мартовского равноденствия фактически находилось в созвездии Овна ; с тех пор он переместился в Рыбы из-за прецессии равноденствий .

См. также

• Формирование и эволюция Солнечной системы
• Неизменная плоскость
• Протопланетный диск
• Небесная система координат

Внешние ссылки

• Эклиптика: годовой путь Солнца по небесной сфере Факультет физики Даремского университета
• Симулятор времен года и эклиптики Университет Небраски-Линкольн
• ИЗМЕРЕНИЕ НЕБА Краткое руководство по небесной сфере Джеймс Б. Калер, Университет Иллинойса
• Времена года Земли. Архивировано 13 октября 2007 г. в Wayback Machine . Военно-морской обсерватории США
• Основы – эклиптика, экватор и системы координат AstrologyClub.Org
• Киносита, Х.; Аоки, С. (1983). «Определение эклиптики». Небесная механика . 31 (4): 329–338. Бибкод : 1983CeMec..31..329K . дои : 10.1007/BF01230290 . S2CID   122913096 . ; сравнение определений Леверье, Ньюкомба и Стэндиша.